Exercícios sobre área do triângulo
A área de um triângulo que possui 12 cm de altura e base medindo 9 cm é:
A) 54 cm²
B) 70 cm²
C) 85 cm²
D) 92 cm²
E) 108 cm²
Alternativa A
Calculando a área do triângulo:
\(A=\frac{b\cdot h}{2}\)
\(A=\frac{12\cdot9}{2}\)
\(A=\ 6\cdot9\ \)
\(A=54\ cm²\)
A área é de 54 cm².
Analise o polígono a seguir:
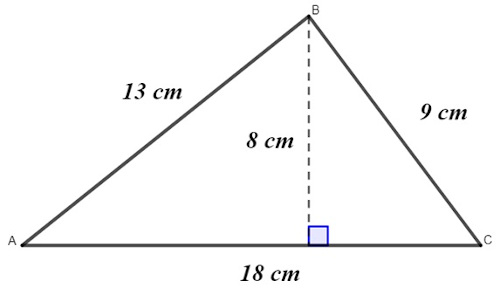
A área desse triângulo é igual a:
A) 36 cm²
B) 52 cm²
C) 64 cm²
D) 72 cm²
E) 81 cm²
Alternativa D
Analisando o polígono da imagem, temos que h = 8 cm e que b = 18 cm. Então, calculando a área:
\(A=\frac{b\cdot h}{2}\)
\(A=\frac{8\cdot18}{2}\)
\(A=8\cdot9\ \)
\(A=72\ cm^2\)
Uma região em um formato de triângulo possui um dos lados medindo 22 metros. Se essa região possui 187 m², a medida da sua altura em metros é:
A) 14 m
B) 15 m
C) 16 m
D) 17 m
E) 18 m
Alternativa D
Sabemos que A = 187 e que b = 22, então:
\(A=\frac{b\cdot h}{2}\)
\(187=\frac{22\cdot h}{2}\)
\(187=11\ h\)
\(\frac{187}{11}=h\)
\(h=17\ \)
A altura deve ser de 17 metros.
Uma peça de um automóvel é produzida no formato de um prisma de base triangular. Em uma de suas bases será colado um adesivo da empresa com indicações sobre a fabricação da peça, cobrindo toda a base. Se essa peça possui lados congruentes medindo 6 cm, utilizando \(\sqrt3=1,7\), então a área dessa região é de:
A) 13,6 cm²
B) 15,4 cm²
C) 17,7 cm²
D) 18,1 cm²
E) 19,0 cm²
Alternativa A
Sabemos que a base desse prisma é composta por um triângulo. Como os lados desse triângulo são congruentes, então esse triângulo é equilátero. Nessas condições, utilizaremos a fórmula do triângulo equilátero para calcular a área.
\(A=\frac{l^2\sqrt3}{4}\)
\(A=\frac{6^2\sqrt3}{4}\)
\(A=\frac{36\sqrt3}{4}\)
\(A=9\sqrt3\)
\(A=9\cdot1,7\)
\(A=13,6\ cm² \)
Um triângulo isósceles possui lados oblíquos medindo 12,5 cm e base medindo 20 cm, então a área desse triângulo é igual a:
A) 6,5
B) 7,0
C) 7,5
D) 8,0
E) 8,5
Alternativa C
Primeiramente, calcularemos a altura do triângulo isósceles, utilizando a relação pitagórica:
\({12,5}^2=h^2+\left(\frac{20}{2}\right)^2\)
\(156,25=h^2+{10}^2\)
\(156,25=h^2+100\)
\(156,25-100=h^2\)
\(56,25=h^2\)
\(\sqrt{56,25}=h\)
\(h=7,5\)
Parte de um terreno no formato triangular possui lados medindo 26 metros, 24 metros e 20 metros, então a área limitada por esse triângulo mede aproximadamente:
A) 239 m²
B) 246 m²
C) 258 m²
D) 262 m²
E) 228 m²
Alternativa D
Como conhecemos a medida dos três lados, utilizaremos a fórmula de Heron:
\(p=\frac{26+24+20}{2}\)
\(p=\frac{70}{2}\)
\(p=35\)
\(A=\sqrt{35\left(35-26\right)\left(35-24\right)\left(35-20\right)}\)
\(A=\sqrt{35\cdot9\cdot11\cdot15}\)
\(A=\sqrt{51975}\)
\(A\approx228\ m² \)
Calculando a área de um triângulo que possui dois lados medindo respectivamente 12 e 9, e o ângulo entre esses dois lados é de 30°, encontraremos:
A) 18 cm²
B) 27 cm²
C) 32 cm²
D) 45 cm²
E) 54 cm²
Alternativa B
Pela lei das áreas, temos que:
\(A=\frac{12⋅9⋅sen30°}{2}\)
\(A=\frac{12\cdot9\cdot0,5}{2}\)
\(A=\frac{54}{2}\)
\(A=27\ cm^2\)
A área desse triângulo é de 27 cm².
Durante o planejamento da construção de um bairro de condomínios, a construtora, junto da prefeitura, planejou a construção de uma praça com formato de um triângulo equilátero. O objetivo é que essa praça tenha 692 m² de área. Utilizando 1,73 como aproximação para \(\sqrt3\), o lado dessa praça deve medir:
A) 25 m
B) 30 m
C) 40 m
D) 45 m
E) 50 m
Alternativa C
Como a praça possui formato de triângulo equilátero, sabemos que:
\(A=\frac{l^2\sqrt3}{4}\)
\(692=\frac{l^2\sqrt3}{4}\)
\(692\cdot4=l^2\cdot1,73\)
\(\frac{2768}{1,73}=l^2\)
\(1600=l^2\)
\(l^2=1600\)
\(l=\sqrt{1600}\)
\(l=40\ \)
O lado dessa praça deve medir 40 metros.
A medida da área do triângulo a seguir é:
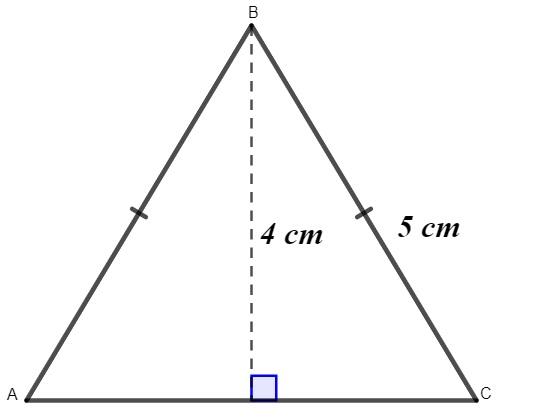
A) 24 cm²
B) 18 cm²
C) 14 cm²
D) 12 cm²
E) 10 cm²
Alternativa D
É necessário calcular a medida da base, mas note que esse triângulo é isósceles, pois ele possui dois lados congruentes. Nessas condições, sendo x a metade da medida da base, e utilizando o teorema de Pitágoras, temos que:
\(5^2=4^2+x^2\)
\(25=16+x^2\)
\(25-16=x^2\)
\(9=x^2\)
\(x^2=9\)
\(x=\sqrt9\)
\(x=3\)
Se metade da base mede 3, a base toda medirá 6 cm. Calculando a área:
\(A=\frac{b\cdot h}{2}\)
\(A=\frac{6\cdot4}{2}\)
\(A=\frac{24}{2}\)
\(A=12\ cm^2\)
(Enem 2010) Em canteiros de obras de construção civil é comum perceber trabalhadores realizando medidas de comprimento e de ângulos e fazendo demarcações por onde a obra deve começar ou se erguer. Em um desses canteiros foram feitas algumas marcas no chão plano. Foi possível perceber que, das seis estacas colocadas, três eram vértices de um triângulo retângulo e as outras três eram os pontos médios dos lados desse triângulo, indicadas por letras.
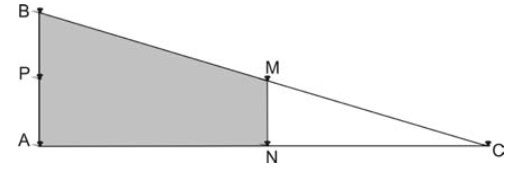
A região demarcada pelas estacas A, B, M e N deveria ser calçada com concreto. Nessas condições, a área a ser calçada corresponde:
A) à mesma área do triângulo AMC.
B) à mesma área do triângulo BNC.
C) à metade da área formada pelo triângulo ABC.
D) ao dobro da área do triângulo MNC.
E) ao triplo da área do triângulo MNC.
Alternativa E
Sabemos que:
\(\overline{AB}=2\overline{MN}\)
\(\overline{AC}=2\overline{CN}\)
Calculando a área do triângulo MNC:
\(A_{\Delta M N C}=\frac{\overline{MN}\cdot\overline{CN}}{2}\)
Ao calcular a área do triângulo ABC, temos que:
\(A_{\Delta A B C}=\frac{\overline{AB}\cdot\overline{AC}}{2}\)
\(A_{\Delta A B C}=\frac{\overline{2MN}\cdot\overline{2CN}}{2}\)
\(A_{\Delta A B C}=4\cdot\frac{\overline{MN}\cdot\overline{CN}}{2}\)
Sabemos que \( A_{\Delta M N C}=\frac{\overline{MN}\cdot\overline{CN}}{2}\):
\(A_{\Delta A B C}=4A_{\Delta M N C}\)
Por outro lado, sabemos que a área do triângulo ABC é igual à soma da área do triângulo MNC com o quadrilátero (região sombreada) ABMN:
\(A_{\Delta A B C}=A_{\Delta M N C}+A_{ABMN}\)
Substituindo a área do triângulo ABC por 4 vezes a área do triângulo MNC:
\(4A_{\Delta M N C}=A_{\Delta M N C}+A_{ABMN}\)
\(4A_{\Delta M N C}-\ A_{\Delta M N C}=A_{ABMN}\)
\(3A_{\Delta M N C}=A_{ABMN}\)
Podemos concluir que a área do quadrilátero ABMN é o trilho da área do triângulo MNC.
(Enem 2012) Para decorar a fachada de um edifício, um arquiteto projetou a colocação de vitrais compostos de quadrados de lado medindo 1 m, conforme a figura a seguir.
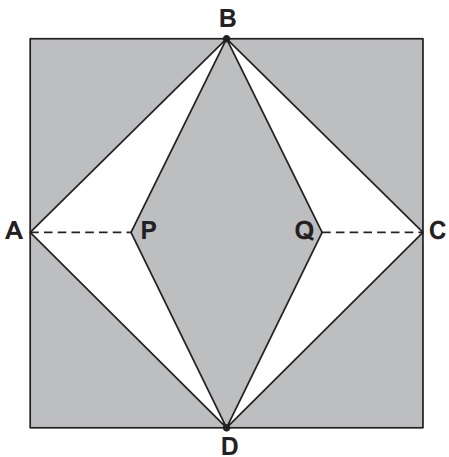
Nessa figura, os pontos A, B, C e D são pontos médios dos lados do quadrado, e os segmentos AP e QC medem 1/4 da medida do lado do quadrado. Para confeccionar um vitral, são usados dois tipos de materiais: um para a parte sombreada da figura, que custa R$ 30 o m², e outro para a parte mais clara (regiões ABPDA e BCDQB), que custa R$ 50 o m². De acordo com esses dados, qual é o custo dos materiais usados na fabricação de um vitral?
A) R$ 22,50
B) R$ 35,00
C) R$ 40,00
D) R$ 42,50
E) R$ 45,00
Alternativa B
Sabemos que a área do vitral toda é igual à área de um quadrado de lado 1, ou seja, 1 m². A região clara é formada por 4 triângulos congruentes, com base medindo 1 : 4 = 0,25 e altura medindo 1 : 2 = 0,5.
Calcular a área da região clara, Ac, é igual a calcular a área de um triângulo e multiplicá-la por 4:
\(Ac=4\cdot\frac{0,25\cdot0,5}{2}\)
\(Ac=2\cdot0,25\cdot0,5\ \)
\(Ac=0,25\ m^2\)
A área da região escura Ae é a diferença entre a área do vitral e a área clara, ou seja:
Ae = 1 – 0,25 = 0,75 m²
Então, o valor gasto será de:
\(0,25\cdot50+0,75\cdot30\)
\(12,5+22,5\ \)
35
Serão gastos R$ 35,00 por vitral.
(Enem 2014 — 2ª aplicação) Um artista deseja pintar em um quadro uma figura na forma de triângulo equilátero ABC de lado 1 metro. Com o objetivo de dar um efeito diferente em sua obra, o artista traça segmentos que unem os pontos médios D, E e F dos lados BC, AC e AB, respectivamente, colorindo um dos quatro triângulos menores, como mostra a figura.
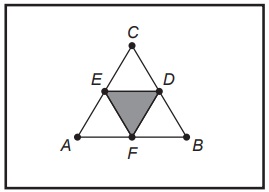
Qual é a medida da área pintada, em metros quadrados, do triângulo DEF?
A) \( \frac{1}{16}\)
B) \( \frac{\sqrt3}{16}\)
C) \( \frac{1}{8}\)
D) \( \frac{3}{8}\)
E) \( \frac{\sqrt3}{4}\)
Alternativa B
É possível perceber que o triângulo ACF foi divido em 4 triângulos congruentes, sendo assim, o triângulo DEF representa \(\frac{1}{4} \) da área do triângulo ABC.
Sabemos que o triângulo ABC tem lado medindo 1 m. Sendo A a área pintada, temos que:
\(A=\frac{l^2\sqrt3}{4}\cdot\frac{1}{4}\)
\(A=\frac{1^2\sqrt3}{4}\cdot\frac{1}{4}\)
\(A=\frac{1\sqrt3}{4}\cdot\frac{1}{4}\)
\(A=\frac{1\sqrt3}{16}\)
\(A=\frac{\sqrt3}{16}\)
