Exercícios sobre equação produto
Das alternativas a seguir, a que contém a quantidade de soluções distintas para a equação (x – 2) (x + 3) (x² – 4) = 0 é:
A) 0
B) 1
C) 2
D) 3
E) 4
Alternativa D
Dada a equação produto (x – 2) (x + 3) (x² – 4) = 0, para que esse produto seja igual a zero, um de seus fatores deve ser zero.
Primeiro fator:
x – 2 = 0 → x = 2
Segundo fator:
x + 3 = 0 → = -3
Terceiro fator:
x² – 4 = 0
x² = 4
x = ± √4
x = ± 2
Então, as soluções são 0, 2 e -2, ou seja, há três soluções.
Analisando a equação a seguir, o número de soluções reais distintas dessa equação é:
x4 + 6x3 + 12x2 + 8x = 0
A) 1
B) 2
C) 3
D) 4
E) 5
Alternativa B
Primeiro vamos fatorar o polinômio, colocando x em evidência:
x4 + 6x3 + 12x2 + 8x = 0
x(x³ + 6x² + 12x + 8) = 0
Note que o segundo termo é o cubo da soma, e que pode ser reescrito por:
x(x + 2)³ = 0
Para que essa equação seja igual a zero, um de seus fatores tem que ser zero.
1º fator:
x = 0
2º fator:
x + 2 = 0 → x = -2
Dessa forma, há duas soluções reais.
A equação do segundo grau x² + 3x – 4 = 0 pode ser representada por uma equação produto, marque a alternativa que corresponde a essa representação:
A) (x + 1) (x + 4) = 0
B) (x – 1) (x + 4) = 0
C) (x + 1) (x – 4) = 0
D) (x – 2) (x + 5) = 0
E) (x + 5) (x – 5) = 0
Alternativa B
Para reescrever a equação do segundo grau como uma equação produto, é necessário encontrar as raízes dessa equação:
x² + 3x – 4 = 0
a = 1
b = 3
c = -4
Δ = b² – 4ac
Δ = 3² – 4 · 1 · (-4)
Δ = 9 + 16
Δ = 25
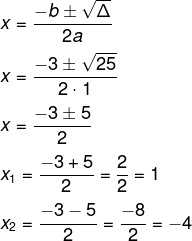
Então, podemos reescrever a equação como a equação produto:
(x – 1) (x + 4) = 0
Uma equação do 2º grau com variável x possui soluções iguais a 5 e -3; a equação do segundo grau que encontramos ao aplicar a propriedade distributiva na equação produto formada por essas raízes é:
A) x² + 2x + 15 = 0
B) x² – 5x + 3 = 0
C) x² + 3x – 5 = 0
D) x² – 2x – 5 = 0
E) x² – 2x – 15 = 0
Alternativa E
Para encontrar a equação do 2º grau, primeiro a escreveremos como uma equação produto:
(x – 5) (x + 3) = 0
Aplicando a propriedade distributiva, temos que:
x² + 3x – 5x – 15 = 0
x² – 2x – 15 = 0
Sabendo que o conjunto S1 é formado pelos números inteiros que satisfazem a equação produto: (12x – 36) (5x – 10) (x + 12) = 0, então, podemos afirmar que:
A) O conjunto S1 é vazio.
B) O conjunto S1 possui três números primos.
C) O conjunto S1 possui dois números positivos.
D) O conjunto S1 possui dois números negativos.
E) O conjunto S1 possui um número par x.
Alternativa C
Primeiro encontraremos as soluções dessa equação. Para que essa equação seja igual a zero, um dos seus fatores tem que ser igual a zero:
1º fator:
12x – 36 = 0
12x = 36
x = 36 : 12
x = 3
2º fator:
5x – 10 = 0
5x = 10
x = 10 : 5
x = 2
3º fator:
x + 12 = 0
x = -12
Então S1: {2, 3, -12}, logo, o conjunto possui dois números positivos como solução.
Das alternativas a seguir, marque aquela em que a equação representada é uma equação produto:
A) (x + 1) (x – 1) + 1 = 0
B) (x² + 2x + 2) = 0
C) (x³ + 2x) + (4x – 3) = 0
D) x (x – 3) = 0
E) 4x + 2y = 3
Alternativa D
A alternativa que corresponde a uma equação produto é a alternativa D.
A soma dos elementos de S, sabendo que S é o conjunto formado pelas soluções da equação (x² – 9) (5x – 15) (2x – 4) = 0, é igual a:
A) 1
B) 2
C) 3
D) 4
E) 5
Alternativa E
Para encontrar as soluções da equação, igualaremos cada um dos seus fatores a zero.
1º fator:
x² – 9 = 0
x² = 9
x = ±√9
x = ± 3
2º fator:
5x – 15 = 0
5x = 15
x = 15 : 5
x = 3
3º fator:
2x – 4 = 0
2x = 4
x = 4 : 2
x = 2
Realizando a soma das soluções, temos que:
-3 + 3 + 3 + 2 = 5
Os números 1, 3 e -4 são soluções da equação:
A) (x + 1) (x + 3) (x – 4) = 0
B) (x – 1) (x – 3) (x – 4) = 0
C) (x – 1) (x – 3) (x + 4) = 0
D) (x + 1) (x + 3) (x + 4) = 0
Alternativa C
Como 1, 3 e -4 são soluções da equação, então, os seus fatores são (x – 1), (x – 3) e (x + 4), pois 1, 3 e -4 são soluções da equação, então, a equação desejada é:
(x – 1) (x – 3) (x + 4) = 0
A quantidade de números inteiros que satisfazem a equação é:
![]()
A) 0
B) 1
C) 2
D) 3
E) 4
Alternativa C
Para encontrar as soluções, vamos igualar cada um dos fatores a zero:
Primeiro fator:
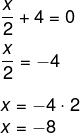
Segundo fator:
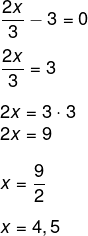
Terceiro fator:
x + 2 = 0
x = -2
Note que, das soluções, são números inteiros o -8 e o -2, logo, há dois números inteiros que são soluções da equação.
Sobre a equação (x – 4) (x² + 3) (5x – 2) = 0, julgue as afirmativas a seguir:
I → Das soluções, somente uma solução pertence ao conjunto dos números naturais;
II → Existem apenas duas soluções reais;
III → É uma equação produto.
Marque a alternativa correta:
A) Somente a I é falsa.
B) Somente a II é falsa.
C) Somente a III é falsa.
D) Todas as afirmativas são verdadeiras.
Alternativa D
Primeiro encontraremos o conjunto de soluções reais da equação (x – 4) (x² + 3) (5x – 2) = 0, igualando cada um dos fatores a zero:
1º fator:
x – 4 = 0
x = 4
2º fator:
x² + 3 = 0
x² = -3
A equação não possui solução real.
3º fator:
5x – 2 = 0
5x = 2
x = 2 : 5
x = 0,4
Então, o conjunto de soluções é S: {0, 4, 4}. Analisando esse conjunto de soluções agora, é possível julgar as afirmativas:
I → Das soluções, somente uma solução pertence ao conjunto dos números naturais; (verdadeira)
Das soluções, 4 é um número natural.
II → Existem apenas duas soluções reais; (verdadeira)
Há duas soluções reais para a equação.
III → É uma equação produto. (verdadeira)
A equação é uma equação produto.
Marque a alternativa que corresponde à definição correta de equação produto:
A) Equação produto é toda equação que possui multiplicações de polinômios no primeiro membro da equação e um número real qualquer no segundo membro.
B) Equação produto é toda equação do 3º grau que possui soluções reais.
C) Equação produto é toda equação que possui somente multiplicações de polinômios em um dos membros da equação igualados a zero.
D) Equação produto é toda equação que possui pelo menos uma multiplicação em um de seus membros.
E) Equação produto é toda equação que possui, como conjunto de soluções, números pertencentes ao conjunto dos números reais.
Alternativa C
A alternativa que define corretamente o que é uma equação produto é a alternativa C.
O conjunto de soluções da equação 3x³ – 48x = 0 é:
A) S: {0, 4}
B) S: {0, -4}
C) S: {-4, 0, 4}
D) S: {4, -4}
E) S: {0}
Alternativa C
Para encontrar as soluções da equação, primeiro vamos colocar o 3x em evidência:
3x(x² – 16) = 0
Então, temos que:
3x = 0 ou x² – 16 = 0
Primeiro fator:
3x = 0 → x = 0
Segundo fator:
x² – 16
x² = 16
x = ±√16
x = ± 4
Então, o conjunto de soluções é S: {-4, 0, 4}.






