Exercícios sobre equações logarítmicas
Resolva a equação logarítmica abaixo, determinando o valor de x:
log10 (4x – 2) = log10 2 – log10 (2x – 1)
Verificando as condições de existência dos logaritmos, temos:
4x – 2 > 0
4x > 2
x > 2
4
x > 1
2
2x – 1 > 0
2x > 1
x > 1
2
A subtração de logaritmos de mesma base pode ser expressa como um quociente. Sendo assim, vamos reescrever a equação:
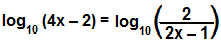
log10 (4x – 2) = log10 2 – log10 (2x – 1)
Como temos uma igualdade de logaritmos de mesma base, podemos desconsiderar os logaritmos e igualar os logaritmandos:
4x – 2 = 2
2x – 1
(4x – 2)(2x – 1) = 2
8x² – 8x + 2 = 2
8x² – 8x = 0
8(x² – x) = 0
x² – x = 0
x1 = 0
x2 = 1
Podemos desconsiderar o x1 = 0, pois a condição de existência dos logaritmos dessa expressão mostra-nos que x > ½. Portanto, o único valor de x para o qual a igualdade log10 (4x – 2) = log10 2 – log10 (2x – 1) é válida é x = 1.
Resolva a equação logarítmica log2x + 1 (10x – 3) = 1.
Vamos verificar as condições de existência do logaritmo:
2x + 1 > 0
2x > – 1
x > – 1/2
10x – 3 > 0
10x > 3
x > 3/10
Aplicando a propriedade básica do logaritmo, temos:
log2x + 1 (10x – 3) = 1
(2x + 1)1 = 10x – 3
2x + 1 = 10x – 3
2x – 10x = – 3 – 1
– 8x = – 4 (– 1)
8x = 4
x = 4
8
x = 1
2
Portanto, a única solução possível para log2x + 1 (10x – 3) = 1 é x = ½.
(Vunesp) O valor de x na equação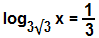 é:
é:
a) 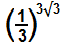
b) 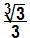
c) 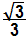
d) 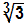
e) √3
Para resolver a equação logarítmica em questão, aplicaremos o princípio básico dos logaritmos:
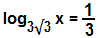
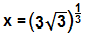
Sabendo que 3√3 = √3³, temos:
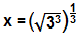
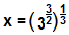
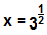
x = √3
Portanto, a solução da equação logarítmica 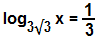 é x = √3. A alternativa correta é a letra e.
é x = √3. A alternativa correta é a letra e.
(FURG-RS) Sendo x a solução da equação 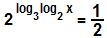 , o valor de x3 é:
, o valor de x3 é:
a) ½
b) 1
c) 2
d) 4
e) 8
A fração ½ pode ser escrita como 2 – 1:
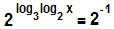
Como as bases estão iguais, podemos estabelecer uma igualdade entre os expoentes:
log3 log2 x = – 1
Resolvendo o primeiro logaritmo, cuja base é 3, temos:
log3 (log2 x) = – 1
3 – 1 = log2 x
log2 x = 1
3
Aplicando novamente o logaritmo, podemos determinar o valor de x:
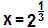
Conforme foi pedido no enunciado, vamos calcular o valor de x³:
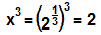
Portanto, a alternativa correta é a letra c.






