Exercícios sobre inequações exponenciais
Se x é um número real, resolva a inequação exponencial (3x)x – 1 ≤ 729.
Podemos reescrever essa inequação exponencial substituindo o número 729 pela potência de base 3 e expoente 6. Feito isso, estabeleceremos a inequação apenas entre os expoentes:
(3x)x – 1 ≤ 729
(3x)x – 1 ≤ 36
x(x – 1) ≤ 6
x² – x – 6 ≤ 0
Agora utilizaremos a fórmula de Bhaskara:
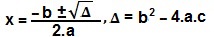
Δ = (– 1)² – 4.1.(– 6)
Δ = 1 + 24
Δ = 25
x = – (– 1) ± √25
2.1
x = 1 ± 5
2
|
x' = 1 + 5 = 6 = 3 x'' = 1 – 5 = – 4 = – 2 |
 |
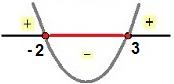Portanto, a solução da inequação é dada por S = {x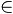 
R | – 2 ≤ x ≤ 3}.
Seja x um número real, determine o conjunto solução da seguinte inequação exponencial:
22x + 2 – 2 x + 3 > 2x – 2
Para resolver a inequação exponencial 22x + 2 – 2 x + 3 > 2x – 2, começaremos separando as potências que apresentam somas no expoente, escrevendo-as como produto de potências.
22x · 22 – 2x · 23 > 2x – 21
(2x)2 · 22 – 2x · 23 > 2x – 21
Façamos y = 2x:
y2 · 22 – y · 23 > y – 21
4y2 – 8y > y – 2
4y2 – 9y + 2 > 0
Temos então uma inequação do 2° grau, que pode ser resolvida pela fórmula de Bhaskara:
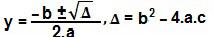
∆ = b² – 4.a.c
∆ = (– 9)² – 4.4.2
∆ = 81 – 32
∆ = 49
y = – b ± √∆
2.a
y = – (– 9) ± √49
2.4
y = 9 ± 7
8
|
y1 = 9 + 7 y1 = 16 y1 = 2 |
y2 = 9 – 7 y2 = 2 y2 = 1 |
Agora que encontramos os possíveis valores de y, podemos resolver y = 2x:
|
Para y1 = 2 2x = y |
Para y2 = 1/4 2x = y |
O enunciado pediu o conjunto solução da inequação exponencial. Como as raízes são x1 = 1 e x2 = – 2, o conjunto solução é S = {x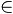 
R | x < – 2 ou x > 1}.
(Vunesp) É dada a inequação:
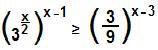
O conjunto verdade V, considerado o conjunto universo como sendo o dos reais, é dado por:
a) V = {x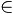 
R | x ≤ – 3 ou x ≥ 2}
b) V = {x 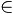R | x ≤ – 3 e x ≥ 2}
c) V = {x 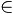R | – 3 ≤ x ≤ 2}
d) V = {x 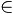R | x ≤ – 3}
e) V = {x 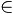R | x ≥ 2}
Para resolver a inequação exponencial proposta no exercício, simplificaremos a fração 3/9:
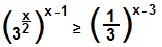
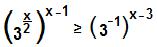
Multiplicaremos agora o expoente que está dentro dos parênteses pelos que estão fora:
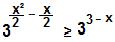
Podemos estabelecer a inequação apenas entre os expoentes:
x² – x ≥ 3 – x
2 2
Multiplicaremos toda a inequação por dois:
x² – x ≥ 6 – 2x
x² + x – 6 ≥ 0
Pela fórmula de Bhaskara, teremos:
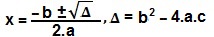
Δ = 1² – 4.1.(– 6)
Δ = 1 + 24
Δ = 25
x = – 1 ± √25
2.1
x = – 1 ± 5
2
|
x' = – 1 + 5 = 4 = 2 x'' = – 1 – 5 = – 6 = – 3 |
 |
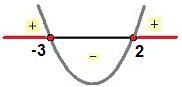Portanto, a alternativa que corresponde à solução encontrada é a letra a.
(UFRGS) A solução da inequação 0,5(1 – x) > 1 é o conjunto:
a) {x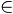 
R | x > 1}
b) {x 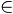R | x < 1}
c) {x 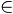R | x > 0}
d) {x 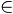R | x < 0}
e) Reais
Inicialmente podemos escrever o número 1 como a potência de base 0,5 e expoente 0:
0,5(1 – x) > 1
0,5(1 – x) > 0,50
Como as bases das potências são iguais, podemos estabelecer a inequação apenas entre os expoentes. Lembrando que, como a base é 0,5, um número menor do que 1, devemos inverter a desigualdade:
1 – x < 0
– x < – 1
x > 1
Portanto, a alternativa que apresenta a solução correta é a letra a.
