Exercícios sobre Matriz
Determine m, n, o e p para que tenhamos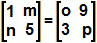 
.
Para valer a igualdade de matrizes, o elemento de uma determinada linha e coluna deverá ser exatamente igual ao elemento que pertence à mesma linha e coluna de outra matriz. Vamos analisar cada elemento:
a11 → o = 1
a12 → m = 9
a21 → n = 3
a22 → p = 5
Dê a matriz A = (aij) 3 x 3, em que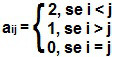 
A matriz A possui três linhas e três colunas da forma 
. Os elementos da diagonal principal são aqueles do tipo aij, em que i = j. A diagonal principal será formada por zeros. Os elementos acima da diagonal principal serão aqueles em que o número da linha é inferior ao número da coluna (i < j) e serão substituídos pelo número 2. Os elementos abaixo da diagonal principal serão aqueles em que i > j e serão substituídos por 1. A matriz resultante será da forma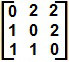 
.
(UDESC) Sendo a matriz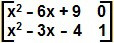 
igual à matriz identidade de ordem 2, o valor de 2.x é:
a) – 4
b) 6
c) 4
d) 8
e) – 8
A matriz identidade é aquela em que a diagonal principal é composta pelo número 1 e os demais elementos são nulos. Podemos afirmar que a igualdade de matrizes é:
= 
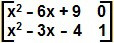Sendo assim, temos duas equações: x2 – 6x + 9 = 1 e x2 – 3x – 4 = 0. Vamos resolvê-las através da fórmula de Bhaskara:
Primeira equação: x2 – 6x + 9 = 1 → x2 – 6x + 8 = 0
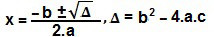
Δ = (– 6)² – 4.1.8
Δ = 36 – 32
Δ = 4
x = – (– 6) ± √4
2.1
x = 6 ± 2
2
x' = 8 = 4
2
x'' = 4 = 2
2
Segunda equação: x2 – 3x – 4 = 0
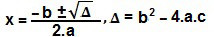
Δ = (– 3)² – 4.1.(– 4)
Δ = 9 + 16
Δ = 25
x = – (– 3) ± √25
2.1
x = 3 ± 5
2
x' = 8 = 4
2
x'' = – 2 = – 1
2
Na resolução das duas equações, obtivemos uma mesma resposta: x' = 4. Se o valor de x é 4, então 2.x = 2.4 = 8. Logo, a alternativa correta é a letra d.
(UERJ) A temperatura corporal de um paciente foi medida, em graus Celsius, três vezes ao dia, durante cinco dias. Cada elemento aij da matriz abaixo corresponde à temperatura observada no instante i do dia j.
Determine:
a) o instante e o dia em que o paciente apresentou a maior temperatura;
b) a temperatura média do paciente no terceiro dia de observação.
a) A maior temperatura da matriz é 40,5 — esse valor está registrado na 2ª linha e 4ª coluna. Sendo assim, podemos dizer que 40,5 corresponde ao elemento matricial a24. Logo, o instante i é 2, enquanto o dia j é 4. Podemos concluir que a maior temperatura do paciente ocorreu no 4° dia e no 2° instante.
b) As temperaturas do terceiro dia estão descritas na terceira coluna. Para calcular a média, devemos somá-las e dividir a soma por 3:
M = 38,6 + 37,2 + 36,1
3
M = 111,9
3
M = 37,3
A média das temperaturas do terceiro dia é 37,3° C.
