Exercícios sobre polinômios
(Enem) Um forro retangular de tecido traz em sua etiqueta a informação de que encolherá após a primeira lavagem mantendo, entretanto, seu formato. A figura a seguir mostra as medidas originais do forro e o tamanho do encolhimento (x) no comprimento e (y) na largura. A expressão algébrica que representa a área do forro após ser lavado é (5 – x) (3 – y).
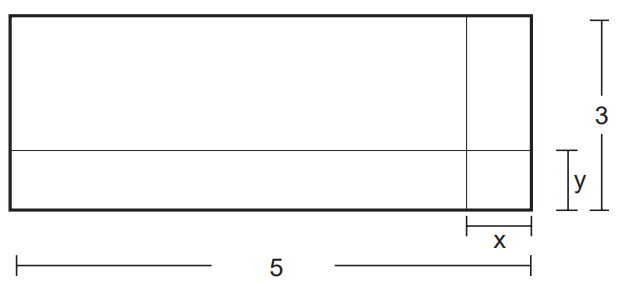
Nessas condições, a área perdida do forro, após a primeira lavagem, será expressa por:
A) 2xy
B) 15 − 3x
C) 15 − 5y
D) -5y − 3x
E) 5y + 3x − xy
Alternativa E
A área perdida pode ser separada em três retângulos.
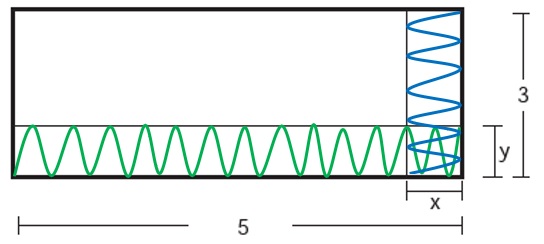
O primeiro retângulo, destacado em verde, tem área 5y, e o segundo retângulo, destacado em azul, tem área 3x, mas note que existe uma região em comum tanto para o retângulo verde quanto para o retângulo azul, de área xy.
Por isso, a área perdida vai ser a soma da área do retângulo em verde com a do retângulo em azul menos a área em comum.
5y + 3x – xy
Dados os polinômios p(x) = 2x³ + 3x² + 1 e q(x) = 3x² + 5x – 15, a soma p(-2) + q(2) é igual a:
A) 1
B) 2
C) 3
D) 4
E) 5
Alternativa D
Primeiro calcularemos o valor numérico de cada um dos polinômios para os valores dados, começando com p(-2):
p(x) = 2x³ + 3x² + 1
p(-2) = 2 · (-2)3 + 3 · (-2)2 + 1
p(-2) = 2 · (-8) + 3 · 4 + 1
p(-2) = -16 + 12 + 1
p(-2) = -3
Agora com q(2):
q(x) = 3x² + 5x – 15
q(2) = 3 · 2² + 5 · 2 – 15
q(2) = 3 · 4 + 10 – 15
q(2) = 12 + 10 – 15
q(2) = 7
Agora calcularemos p(-2) + q(2) = -3 + 7 = 4
(EAM - Aprendiz de marinheiro) Analise a figura a seguir:
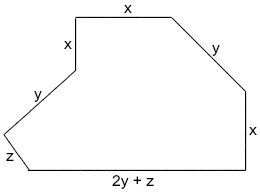
Suponha que o terreno comprado por um proprietário tenha a forma da figura acima e suas medidas sejam representadas, em unidades de comprimento, pelas variáveis X, Y e Z. A expressão algébrica que representa o perímetro desse terreno é:
A) 2x + 3y + z
B) 3x + 4y + 2z
C) 3x + 3y + z
D) 3x + 2y + 3z
E) 4x + 3y + 2z
Alternativa B
O perímetro é a soma de todos os lados da figura:
P = 2y + z + z + y + x + x + y + x
Simplificando o polinômio:
P = 3x + 4y + 2z
Conhecendo o polinômio p(x) = 6x4 + 3x³ – 2x + x5, podemos afirmar que o seu grau é igual a:
A) 4
B) 5
C) 12
D) 11
E) 13
Alternativa B
O grau do polinômio é dado pelo monômio de maior grau. Analisando o polinômio p(x), é possível perceber que o maior expoente é 5, logo, ele possui grau 5.
Sabendo que -3 é raiz do polinômio p(x) = 2x³ + kx², então, o valor de k é igual a:
A) 2
B) 3
C) 4
D) 5
E) 6
Alternativa E
Como -3 é raiz do polinômio, então, p(-3) = 0. Substituindo x = -3 e igualando a zero, temos que:
p(-3) = 2 · (-3)3 + k · (-3)2
p(-3) = 2 · (-27) + k · 9
p(-3) = -54 + k · 9
0 = -54 + 9k
54 = 9k
9k = 54
k = 54 : 9
k = 6
Conhecendo os polinômios a seguir:
P = 3a² + 4ab – 3b²
Q = a² + b²
R = -4a² – 3ab + 2b²
Então, o valor da soma P + Q + R é igual a:
A) ab
B) a² + ab – b²
C) 2a² + 2ab
D) 3a² + 4ab + b²
E) a² – ab
Alternativa A
Realizando a soma, temos que:
P + Q + R = (3a² + 4ab – 3b²) + (a² + b²) + (-4a² – 3ab + 2b²)
Simplificando os termos semelhantes, temos:
P + Q + R = 3a² + 4ab – 3b² + a² + b² – 4a² – 3ab + 2b²
P + Q + R = 0a² + ab + 0b²
P + Q + R = ab
Um terreno possui toda a região coberta de grama, conforme a imagem a seguir:
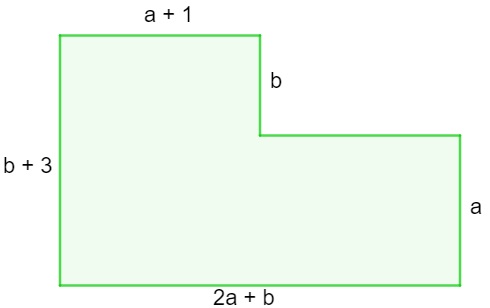
O polinômio que representa o perímetro do polígono é:
A) 4a + 3b
B) 2a – b + 2
C) 4a + 3b + 4
D) 2a + 2b + 1
E) 3b + 4
Alternativa C
O perímetro é a soma de todos os lados da figura, dada por:
P = 2a + b + b + 3 + a + 1 + b + a
P = 4a + 3b + 4
Dados os polinômios P(x) = x² + 3x – 2 e Q(x) = x² – 5, ou seja, M(x) = P(x) · Q(x), então, M(3) é igual a:
A) 65
B) 74
C) 58
D) 64
E) 90
Alternativa D
Primeiro calcularemos o produto entre P(x) e Q(x):
M(x) = (x² + 3x – 2) (x² – 5)
M(x) = x4 – 5x² + 3x³ – 15x – 2x² + 10
M(x) = x4 – 7x² + 3x³ – 15x + 10
Agora calcularemos M(3):
M(3) = 34 – 7 (3)² + 3 (3)³ – 15x + 10
M(3) = 81 – 7 · 9 + 3 · 27 – 15 · 3 + 10
M(3) = 81 – 63 + 81 – 45 + 10
M(3) = 64
Qual deve ser o valor de k, para que o polinômio P(x) = (k² – 16)x4 + (k + 4)x3 + kx² + 2x – 4 tenha grau 2?
A) 4
B) -4
C) ±4
D) 16
E) -16
Alternativa B
Para que o polinômio tenha grau 0, os coeficientes que acompanham x4 e x3 têm que ser iguais a 0, ou seja:
P(x) = (k² – 16)x4 + (k + 4)x3 + kx² + 2x – 4
k² – 16 = 0 e k + 4 = 0
Encontraremos os valores para o primeiro coeficiente:
k² – 16 = 0
k² = 16
k = ± √16
k = ± 4
Agora encontraremos o valor de k para o segundo coeficiente:
k + 4 = 0
k = -4
Como solução para o coeficiente de x4, temos k = ± 4, e para o coeficiente de x3, k = -4. Então, como solução para que os dois coeficientes sejam igual a 0, temos k = -4.
Analise o retângulo a seguir:

Qual é o polinômio que representa a área desse retângulo:
A) 3x + 7
B) x² + 12
C) 2x² + 12
D) 2x² + 10x + 12
E) x² + 5x + 7
Alternativa D
A área do retângulo é o produto entre os lados:
A = (2x + 4) (x + 3)
A = 2x² + 6x + 4x + 12
A= 2x² + 10x + 12
Dados P(x) = x² – x + 6 e D(x) = x – 3, e sendo Q(x) = P(x) : D(x), então, o valor de Q(-2) é:
A) 1
B) 2
C) 0
D) -1
E) -2
Alternativa C
Realizaremos a divisão dos polinômios:
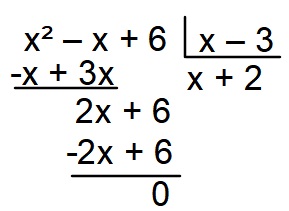
Então, Q(x) = x + 2
Queremos Q(-2) = -2 + 2 = 0
Ao realizar o produto dos polinômios P(x) e Q(x), sabendo que P(x) tem grau 3 e Q(x) tem grau 5, o grau do polinômio P(x) · Q(x) será:
A) 5
B) 8
C) 15
D) 2
E) 9
Alternativa B
Sabendo que o grau de P(x) é 3 e o grau de Q(x) é 5, para saber o grau do polinômio encontrado por meio do produto desses polinômios, basta realizar a soma dos graus, 5 + 3 = 8.






