Exercícios sobre soma dos ângulos internos de um triângulo
(UEM PR/2016) Com base em conhecimentos de Geometria Plana, assinale o que for correto.
01. O quadrado do comprimento do lado maior de um triângulo só é igual à soma dos quadrados dos comprimentos dos demais lados se o ângulo interno oposto ao maior lado é reto.
02. Todo quadrilátero no qual as medidas de todos os lados são as mesmas é um quadrado.
04. A soma das medidas dos ângulos internos de um triângulo é igual a 360 graus.
08. Todo quadrilátero que é um retângulo é, também, um paralelogramo.
16. Em todo triângulo, a soma dos comprimentos de dois lados é sempre maior do que o comprimento do lado restante.
a) A soma dos itens correspondentes às questões erradas é 10.
b) A soma dos itens correspondentes às questões corretas é 25.
c) A soma dos itens correspondentes às questões corretas é 22.
d) A soma dos itens correspondentes às questões corretas é 23.
e) A soma dos itens correspondentes às questões corretas é 31.
01. Correta.
02. Falsa.
Para ser quadrado, também é necessário que o quadrilátero possua ângulos retos.
04. Falsa.
A soma das medidas dos ângulos internos de um triângulo, independentemente do seu formato, tamanho e ângulos, sempre é igual a 180°.
08. Correta.
16. Correta.
Gabarito: Letra B.
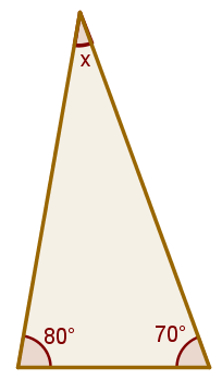
Qual é a medida do ângulo x do triângulo a seguir?
a) 100°
b) 180°
c) 90°
d) 40°
e) 30°
Para resolver essa questão, basta usar a soma dos ângulos internos de um triângulo.
80 + 70 + x = 180
150 + x = 180
x = 180 – 150
x = 30°
Gabarito: alternativa E.
Qual é a medida do ângulo representado por x na figura a seguir?
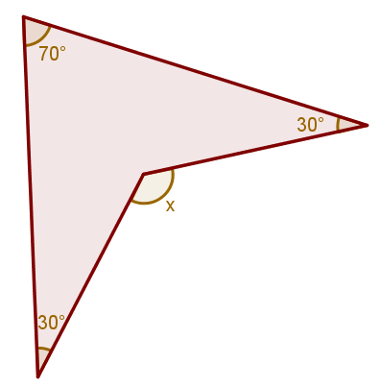
a) 80°
b) 100°
c) 50°
d) 130°
e) 200°
Precisamos dividir esse quadrilátero em dois triângulos, de acordo com a figura a seguir:
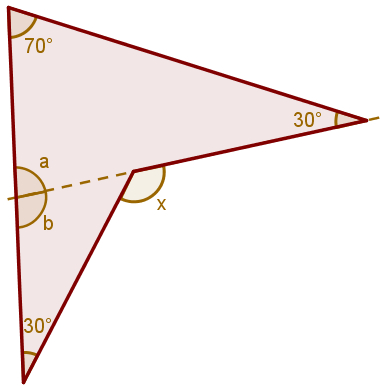
Observe que o ângulo a pode ser obtido pela soma dos ângulos internos de um triângulo:
a + 30 + 70 = 180
a + 100 = 180
a = 180 – 100
a = 80°
O ângulo b, por sua vez, é adjacente ao ângulo a, logo, sua medida é dada por:
a + b = 180
80 + b = 180
b = 180 – 80
b = 100°
O ângulo c é adjacente a x, logo, c + x = 180. Para descobrir c, basta fazer a soma dos ângulos internos do triângulo pequeno:
100 + 30 + c = 180
130 + c = 180
c = 180 – 130
c = 50°
Então:
50 + x = 180
x = 180 – 50
x = 130°
O ângulo x é igual a 130°.
Gabarito: alternativa D.
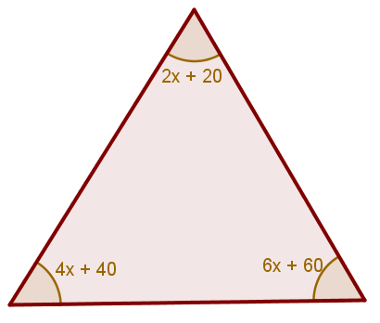
Qual é o valor de x no triângulo a seguir?
a) 5
b) 6
c) 7
d) 12
e) 120
Para encontrar o valor de x, utilize a soma dos ângulos internos de um triângulo:
2x + 20 + 4x + 40 + 6x + 60 = 180
12x = 180 – 120
12x = 60
x = 60
12
x = 5
Gabarito: alternativa A.





