Exercícios sobre função horária do MUV
Teste seus conhecimentos por meio desta lista de exercícios sobre função horária do MUV, que pode ser da posição ou da velocidade.
(Unifesp) A velocidade em função do tempo de um ponto material em movimento retilíneo uniformemente variado, expressa em unidades do SI, é v=50-10∙t.
Pode-se afirmar que, no instante t = 5,0 s, esse ponto material tem:
A) velocidade e aceleração nulas.
B) velocidade nula e daí em diante não se movimenta mais.
C) velocidade nula e aceleração a = -10 m/s2.
D) velocidade nula e a sua aceleração muda de sentido.
E) aceleração nula e a sua velocidade muda de sentido.
(FEI) No movimento retilíneo uniformemente variado, com velocidade inicial nula, a distância percorrida é:
A) diretamente proporcional ao tempo de percurso.
B) inversamente proporcional ao tempo de percurso.
C) diretamente proporcional ao quadrado do tempo de percurso.
D) inversamente proporcional ao quadrado do tempo de percurso.
E) diretamente proporcional à velocidade.
(Fuvest) Um veículo parte do repouso em movimento retilíneo e acelera com aceleração escalar constante e igual a 2,0 m/s2. Pode-se dizer que sua velocidade escalar e a distância percorrida após 3,0 segundos valem, respectivamente:
A) 6,0 m/s e 9,0 m
B) 6,0m/s e 18 m
C) 3,0 m/s e 12 m
D) 12 m/s e 35 m
E) 2,0 m/s e 12 m
(Uern) Seja o gráfico da velocidade em função do tempo de um corpo em movimento retilíneo uniformemente variado representado abaixo.
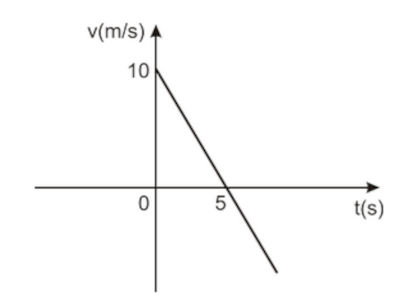
Considerando a posição inicial desse movimento igual a 46 m, então a posição do corpo no instante t = 8 s é:
A) 54 m.
B) 62 m.
C) 66 m.
D) 74 m.
Determine a aceleração de um ciclista que partiu do repouso e atingiu uma velocidade de 36 km/h em 5s?
A) 0,5 m/s2
B) 1,0 m/s2
C) 1,5 m/s2
D) 2,0 m/s2
E) 2,5 m/s2
Um carro parte do respouso e desloca 2000 m durante 50 segundos, então a sua aceleração será:
A) 0,8 m/s2
B) 1,0 m/s2
C) 1,2 m/s2
D) 1,4 m/s2
E) 1,6 m/s2
Quanto tempo demorou para que um carro saísse do repouso e atingisse uma velocidade de 100 m/s, considerando que sua aceleração foi de 2,5 m/s2?
A) 40 s
B) 50 s
C) 60 s
D) 70 s
E) 80 s
Qual foi a variação de deslocamento depois de 2 segundos, quando uma pessoa partiu do repouso e adquiriu uma aceleração de 5 m/s2?
A) 8 m
B) 10 m
C) 12 m
D) 14 m
E) 16 m
Uma bike atingiu uma velocidade final de 48 m/s após 10 segundos, com uma aceleração de 0,8 m/s2, então qual era a sua velocidade inicial?
A) 30 m/s
B) 35 m/s
C) 40 m/s
D) 45 m/s
E) 50 m/s
Um motociclista, partindo do repouso, se locomoveu 6400 metros em um tempo t. Sabendo que a sua aceleração era de 8 m/s2, calcule esse tempo.
A) 10 s
B) 20 s
C) 30 s
D) 40 s
E) 50 s
Calcule a aceleração de um automóvel, inicialmente em repouso, que demorou 32 s para atingir uma velocidade de 288 km/h .
A) 0,5 m/s2
B) 1,0 m/s2
C) 1,5 m/s2
D) 2,0 m/s2
E) 2,5 m/s2
Qual(is) das alternativas apresenta(m) a unidade de medida correspondente à grandeza física estudada na função horária do MUV:
I. A aceleração é medida em metros por segundo ao quadrado.
II. A velocidade é medida em metros por segundo.
III. O deslocamento é medido em metros por segundo.
IV. O tempo é medido em segundo ao quadrado.
A) Alternativas I e II.
B) Alternativas III e IV.
C) Alternativas I e III.
D) Alternativas II e IV.
E) Alternativas I e IV.
Alternativa C.
Primeiramente, calcularemos a velocidade empregando a função horária da velocidade dada no enunciado:
\(v = 50 - 10 \cdot t\\ v = 50 - 10 \cdot 5\\ v = 50 - 50\\ v = 0 \, \text{m/s} \)
Por fim, calcularemos a aceleração média empregando a sua fórmula:
\(a_m = \frac{\Delta v}{\Delta t}\\ a_m = \frac{v_f - v_i}{t_f - t_i}\\ a_m = \frac{0 - 50}{5 - 0}\\ a_m = \frac{-50}{5}\\ a_m = -10 \, \text{m/s}^2\)
Alternativa C.
Para encontrarmos a resposta, é necessário analisar a fórmula da função horária da posição no MUV:
\(x_f = x_i + v_i \cdot t + \frac{a \cdot t^2}{2} \)
Com a velocidade inicial nula:
\(x_f = x_i + 0 \cdot t + \frac{a \cdot t^2}{2}\\ x_f = x_i + \frac{a \cdot t^2}{2}\\ x_f - x_i = \frac{a \cdot t^2}{2}\\ \Delta x = \frac{a \cdot t^2}{2} \)
Portanto, o deslocamento é diretamente proporcional à aceleração e ao quadrado do tempo.
Alternativa A.
Primeiramente, calcularemos a velocidade final empregando a fórmula da função horária da velocidade no MUV:
\(v_f = v_i + a \cdot t \\ v_f = 0 + 2 \cdot 3 \\ v_f = 6 \, \text{m/s}\)
Por fim, calcularemos a distância percorrida empregando a fórmula da função horária da posição no MUV:
\(x_f = x_i + v_i \cdot t + \frac{a \cdot t^2}{2} \\ x_f = 0 + 0 \cdot 3 + \frac{2 \cdot 3^2}{2} \\ x_f = 0 + 0 + \frac{2 \cdot 9}{2} \\ x_f = 9 \, \text{m}\)
Alternativa B.
Primeiramente, calcularemos a aceleração média empregando a sua fórmula:
\(a_m = \frac{\Delta v}{\Delta t} \\ a_m = \frac{v_f - v_i}{t_f - t_i} \\ a_m = \frac{0 - 10}{5 - 0} \\ a_m = \frac{-10}{5} \\ a_m = -2 \, \text{m/s}^2 \)
Por fim, calcularemos a posição final em 8 segundos empregando a fórmula da função horária da posição no MUV:
\(x_f = x_i + v_i \cdot t + \frac{a \cdot t^2}{2} \\ x_f = 46 + 10 \cdot 8 + \frac{(-2) \cdot 8^2}{2} \\ x_f = 46 + 80 - 64 \\ x_f = 62 \, \text{m} \)
Alternativa D.
Primeiramente, converteremos de km/h para m/s :
Por fim, calcularemos a aceleração empregando a fórmula da função horária da velocidade no MUV:
\(v_f = v_i + a \cdot t \\ 10 = 0 + a \cdot 5 \\ 10 = a \cdot 5 \\ a = \frac{10}{5} \\ a = 2 \, \text{m/s}^2 \)
Alternativa E.
Calcularemos a aceleração empregando a fórmula da função horária da posição no MUV:
\(x_f = x_i + v_i \cdot t + \frac{a \cdot t^2}{2} \\ x_f - x_i = v_i \cdot t + \frac{a \cdot t^2}{2} \\ \Delta x = v_i \cdot t + \frac{a \cdot t^2}{2} \\ 2000 = 0 \cdot 50 + \frac{a \cdot 50^2}{2} \\ 2000 = 0 + \frac{a \cdot 2500}{2} \\ 2000 = a \cdot 1250 \\ a = \frac{2000}{1250} \\ a = 1,6 \, \text{m/s}^2 \)
Alternativa A.
Calcularemos o tempo empregando a fórmula da função horária da velocidade no MUV:
\(v_f = v_i + a \cdot t \\ 100 = 0 + 2,5 \cdot t \\ 100 = 2,5 \cdot t \\ t = \frac{100}{2,5} \\ t = 40 \, \text{s} \)
Alternativa B.
Calcularemos a variação de deslocamento empregando a fórmula da função horária da posição no MUV:
\(x_f = x_i + v_i \cdot t + \frac{a \cdot t^2}{2} \\ x_f - x_i = v_i \cdot t + \frac{a \cdot t^2}{2} \\ \Delta x = v_i \cdot t + \frac{a \cdot t^2}{2} \\ \Delta x = 0 \cdot 2 + \frac{5 \cdot 2^2}{2} \\ \Delta x = 0 + \frac{5 \cdot 4}{2} \\ \Delta x = 10 \, \text{m} \)
Alternativa C.
Calcularemos a velocidade inicial empregando a fórmula da função horária da velocidade no MUV:
\(v_f = v_i + a \cdot t \\ 48 = v_i + 0,8 \cdot 10 \\ 48 = v_i + 8 \\ v_i = 48 - 8 \\ v_i = 40 \, \text{m/s} \)
Alternativa D.
Calcularemos o tempo empregando a fórmula da função horária da posição no MUV:
\(x_f = x_i + v_i \cdot t + \frac{a \cdot t^2}{2} \\ x_f - x_i = v_i \cdot t + \frac{a \cdot t^2}{2} \\ \Delta x = v_i \cdot t + \frac{a \cdot t^2}{2} \\ 6400 = 0 \cdot t + \frac{8 \cdot t^2}{2} \\ 6400 = 0 + 4 \cdot t^2 \\ 6400 = 4 \cdot t^2 \\ t^2 = \frac{6400}{4} \\ t^2 = 1600 \\ t = \sqrt{1600} \\ t = 40\ \text{s} \)
Alternativa E.
Primeiramente, transformaremos a aceleração do automóvel de km/h para m/s :
Por fim, calcularemos a sua aceleração empregando a fórmula da função horária da velocidade no MUV:
\(v_f = v_i + a \cdot t \\ 80 = 0 + a \cdot 32 \\ 80 = a \cdot 32 \\ a = \frac{80}{32} \\ a = 2,5 \, \text{m/s}^2 \)
Alternativa A.
I. A aceleração é medida em metros por segundo ao quadrado. (correta)
II. A velocidade é medida em metros por segundo. (correta)
III. O deslocamento é medido em metros por segundo. (incorreta)
O deslocamento é medido em metros.
IV. O tempo é medido em segundo ao quadrado. (incorreta)
O tempo é medido em segundos.


