Exercícios sobre associação de resistores em paralelo
Teste seus conhecimentos por meio desta lista de exercícios sobre associação de resistores em paralelo, associação em que todos os resistores estão em diferentes fios.
Publicado por: Pâmella Raphaella MeloQuestões
-
Questão 1
(PUC) Três resistores idênticos de R = 30Ω estão ligados em paralelo com uma bateria de 12 V. Pode-se afirmar que a resistência equivalente do circuito é de:
A) Req = 10Ω, e a corrente é 1,2 A.
B) Req = 20Ω, e a corrente é 0,6 A.
C) Req = 30Ω, e a corrente é 0,4 A.
D) Req = 40Ω, e a corrente é 0,3 A.
E) Req = 60Ω, e a corrente é 0,2 A.
Alternativa A.
Primeiramente, calcularemos a resistência equivalente da associação de resistores em paralelo empregando a fórmula da resistência elétrica equivalente para uma associação de resistores em paralelo com todos os resistores possuindo o mesmo valor de resistência elétrica:
\(R_{eq} = \frac{R}{n}\)
\(R_{eq} = \frac{30}{3}\)
\(R_{eq}=10 Ω\)
Por fim, calcularemos a corrente elétrica empregando a fórmula da priameir lei de Ohm:
U = R ∙ i
12 = 10 ∙ i
i = \(\frac{12}{10}\)
i = 1,2 A
-
Questão 2
(Vunesp) Um indivíduo deseja fazer com que o aquecedor elétrico central de sua residência aqueça a água do reservatório no menor tempo possível. O aquecedor possui um resistor com resistência R. Contudo, ele possui mais dois resistores exatamente iguais ao instalado no aquecedor e que podem ser utilizados para esse fim. Para que consiga seu objetivo, tomando todas as precauções para evitar acidentes, e considerando que as resistências não variem com a temperatura, ele deve utilizar o circuito
A)
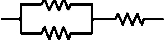
B)
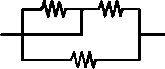
C)
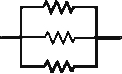
D)

E)
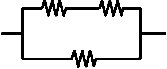
Alternativa C.
Para que o indivíduo consiga o seu objetivo, ele deve utilizar o circuito em que todas as associações estão em paralelo, assim, a água se aquecerá no menor tempo possível.
-
Questão 3
(Mack) Um certo resistor de resistência elétrica R, ao ser submetido a uma d.d.p. de 6,00 V, é percorrido por uma corrente elétrica de intensidade 4,00 mA. Se dispusermos de três resistores idênticos a este, associados em paralelo entre si, teremos uma associação cuja resistência elétrica equivalente é:
A) 4,5 kΩ
B) 3,0 kΩ
C) 2,0 kΩ
D) 1,5 kΩ
E) 0,5 kΩ
Alternativa E.
Primeiramente, calcularemos a resistência de cada resistor empregando a fórmula da primeira lei de Ohm:
U = R ∙ i
6 = R ∙ 4 ∙ 10-3
\(R = \frac{6}{4 \cdot 10^{-3}} \)
R = 1500 Ω
Por fim, calcularemos a resistência equivalente na associação de resistores em paralelo empregando a fórmula da resistência elétrica equivalente para uma associação de resistores em paralelo com todos os resistores possuindo o mesmo valor de resistência elétrica:
\(R_{eq} = \frac{R}{n} \)
\(R_{eq} = \frac{1500}{3} \)
R = 500
R = 0,5 kΩ
-
Questão 4
(UEL) Um resistor de 10Ω no qual flui uma corrente elétrica de 3,0 ampères está associado em paralelo com outro resistor. Sendo a corrente elétrica total, na associação, igual a 4,5 ampères, o valor do segundo resistor, em ohms, é:
A) 5,0
B) 10
C) 20
D) 30
E) 60
Alternativa C.
Primeiramente, calcularemos a tensão elétrica no resistor de 10 Ω quando ele é percorrido pela corrente elétrica de 3 A, empregando a fórmula da primeira lei de Ohm:
U = R ∙ i
U = 10 ∙ 3
U = 30 V
Por fim, calcularemos a resistência elétrica do segundo resistor, que terá tensão elétrica igual à tensão elétrica do primeiro resistor, empregando a fórmula da primeira lei de Ohm:
U = R ∙ i
Vale lembrar que a corrente elétrica do segundo resistor é a subtração da corrente elétrica total com a corrente elétrica do primeiro resistor, então:
30 = R ∙ (4,5 - 3)
30 = R ∙ 1,5
R = \(\frac{30}{1,5}\)
R = 20Ω
-
Questão 5
A associação de resistores em paralelo apresenta diversas propriedades. A partir disso, analise as propriedades abaixo:
I. Mesma corrente elétrica atravessando os resistores.
II. Diferentes valores de corrente elétrica atravessando os resistores.
III. Mesma DDP nos terminais de cada resistor.
IV. Diferentes valores de DDP nos terminais de cada resistor.
Quais propriedades estão corretas?
A) I e III.
B) II e IV
C) I e IV
D) II e III.
E) Todas estão corretas.
Alternativa D.
Na associação de resistores em paralelo, temos a passagem da mesma DDP nos terminais de cada resistor, contudo, cada resistor apresenta um diferente valor de corrente elétrica.
-
Questão 6
Determine a resistência elétrica equivalente de dois resistores de 10Ω cada, associados em paralelo.
A) 0 Ω
B) 5 Ω
C) 10 Ω
D) 15 Ω
E) 20 Ω
Alternativa B.
Calcularemos a resistência elétrica equivalente da associação de resistores em paralelo empregando a sua fórmula:
\(R_{eq} = \frac{R_1 \ \cdot \ R_2}{R_1 + R_2} \)
\(R_{eq} = \frac{10 \cdot 10}{10 + 10}\)
\(R_{eq} = \frac{100}{20}\)
Req = 5 Ω
-
Questão 7
A associação de resistores em paralelo é usada nas situações em que, caso ocorra queima de algum dos resistores, todos os outros não sejam queimados. Então, dentre as alternativas abaixo, em qual delas não temos a aplicação de associações de resistores em paralelo?
A) Circuitos elétricos.
B) Iluminação pública.
C) Equipamentos eletrônicos.
D) Luzes residenciais.
E) Pisca-pisca.
Alternativa D.
Os pisca-piscas não são constituidos de associações de resistores em paralelo, apenas de associações de resistores em série.
-
Questão 8
Três resistores de resistência elétrica 8 Ω, 12 Ω e 16 Ω estão associados em paralelo. Calcule a sua resistência elétrica equivalente.
A) 1,23 Ω
B) 2,46 Ω
C) 3,69 Ω
D) 4,82 Ω
E) 5,05 Ω
Alternativa C.
Calcularemos a resistência elétrica equivalente da associação de resistores em paralelo empregando a fórmula geral:
\(\frac{1}{R_{eq}} = \frac{1}{R_1} + \frac{1}{R_2} + \cdots + \frac{1}{R_N} \)
\(\frac{1}{R_{eq}} = \frac{1}{8} + \frac{1}{12} + \frac{1}{16} \)
\(\frac{1}{R_{eq}} = 0,1250 + 0,0833 + 0,0625 \)\(\frac{1}{R_{eq}} = 0,27083 \)
\(R_{eq} = \frac{1}{0,27083} \)
\(R_{eq} \cong 3,69 \,\Omega\)
-
Questão 9
Considere um circuito elétrico contendo três resistores associados em paralelo, com resistência elétrica de 1 Ω, de 2 Ω e de 2,5 Ω. Calcule a corrente elétrica que os atravessa quando eles são conectados a uma bateria de 50 V.
A) 96,15 A
B) 98,64 A
C) 100,45 A
D) 102,74 A
E) 104,93 A
Alternativa A.
Primeiramente, calcularemos a resistência elétrica equivalente da associação de resistores em paralelo empregando a fórmula geral:
\(\begin{align*} \frac{1}{R_{\rm eq}} &= \frac{1}{R_1} + \frac{1}{R_2} + \cdots + \frac{1}{R_N} \\ \frac{1}{R_{\rm eq}} &= \frac{1}{1} + \frac{1}{2} + \frac{1}{2,5} \\ \frac{1}{R_{\rm eq}} &= 1 + 0,5 + 0,4 \\ \frac{1}{R_{\rm eq}} &= 1,9 \\ R_{\rm eq} &= \frac{1}{1,9} \\ R_{\rm eq} &\cong 0,52 \ \Omega \end{align*} \)
Por fim, calcularemos a corrente elétrica que atravessa os resistores através da fórmula da primeira lei de Ohm:
U = R ∙ i
50 = 0,52 ∙ i
i = \(\frac{50}{0,52} \)
i \(\cong\) 96,15 A
-
Questão 10
Uma corrente elétrica de 6 A percorre dois resistores associados em paralelo. Sabendo que a resistência elétrica dos resistores são 5 Ω e 10 Ω, qual é a DDP em cada um desses resistores, respectivamente?
A) 20 V e 40 V
B) 30 V e 60 V
C) 40 V e 80 V
D) 50 V e 100 V
E) 60 V e 120 V
Alternativa B.
Primeiramente, calcularemos a DDP nos terminais do resistor 1 empregando a fórmula da primeira lei de Ohm:
U1 = R1 ∙ i
U1 = 5 ∙ 6
U1 = 30 V
Por fim, calcularemos a DDP nos terminais do resistor 2 empregando a fórmula da primeira lei de Ohm:
U2 = R2 ∙ i
U2 = 10 ∙ 6
U2 = 60 V
-
Questão 11
Um circuito elétrico possui 10 resistores elétricos associados em paralelo. Sabendo que as resistências elétricas dos resistores vão de 1 Ω a 10 Ω, calcule a resistência elétrica equivalente dessa associação.
A) 0,126 Ω
B) 0,174 Ω
C) 0,224 Ω
D) 0,268 Ω
E) 0,342 Ω
Alternativa E.
Calcularemos a resistência elétrica equivalente da associação de resistores em paralelo empregando a fórmula geral:
\(\frac{1}{R_{\rm eq}} = \frac{1}{R_1} + \frac{1}{R_2} + \cdots + \frac{1}{R_N} \\[2mm] \frac{1}{R_{\rm eq}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \frac{1}{R_4} + \frac{1}{R_5} + \frac{1}{R_6} + \frac{1}{R_7} + \frac{1}{R_8} + \frac{1}{R_9} + \frac{1}{R_{10}} \\[2mm] \frac{1}{R_{\rm eq}} = \frac{1}{1} + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6} + \frac{1}{7} + \frac{1}{8} + \frac{1}{9} + \frac{1}{10} \\[2mm] \frac{1}{R_{\rm eq}} = 1 + 0,50 + 0,33 + 0,25 + 0,20 + 0,16 + 0,14 + 0,125 + 0,11 + 0,10 \\ \frac{1}{R_{\rm eq}} = 2,929 \\ R_{\rm eq} = \frac{1}{2929} \\ R_{\rm eq} \cong 0,342 Ω\)
-
Questão 12
Quais das afirmações abaixo apresentam as unidades de medidas correspondentes às grandezas físicas estudadas na associação de resistores em paralelo?
I. A corrente elétrica é medida em Ámpere.
II. A tensão elétrica é medida em Volt.
III. A resistência elétrica é medida em Ohm.
IV. A carga elétrica é medida em Coulomb por Ampére.
V. A resistência elétrica equivalente é medida em Ohm ao quadrado.
Está(ão) correta(s):
A) I, II e III.
B) I, IV, V.
C) II, III, IV.
D) I, II,V
E) III, IV, V
Alternativa A.
I. A corrente elétrica é medida em Ámpere. (correta)
II. A tensão elétrica é medida em Volt. (correta)
III. A resistência elétrica é medida em Ohm. (correta)
IV. A carga elétrica é medida em Coulomb por Ampére. (incorreta)
A carga elétrica é medida em Coulomb.
V. A resistência elétrica equivalente é medida em Ohm ao quadrado. (incorreta)
A resistência elétrica equivalente é medida em Ohm.