Exercícios sobre Calorimetria
Teste seus conhecimentos com esta lista de exercícios sobre Calorimetria, a área da Física que estuda as trocas de calor e os fenômenos relacionados a ele.
Publicado por: Pâmella Raphaella MeloQuestões
-
Questão 1
(UFPR) Para aquecer 500 g de certa substância de 20 °C para 70 °C, foram necessárias 4000 calorias. A capacidade térmica e o calor específico valem, respectivamente:
A) 8 cal/ °C e 0,08 \(\frac{cal}{g °C}\)
B) 80 cal/ °C e 0,16 \(\frac{cal}{g °C}\)
C) 90 cal/ °C e 0,09 \(\frac{cal}{g °C}\)
D) 95 cal/ °C e 0,15 \(\frac{cal}{g °C}\)
E) 120 cal/ °C e 0,12 \(\frac{cal}{g °C}\)
Alternativa B
Encontraremos o valor da capacidade térmica por meio da fórmula:
\(C=\frac{Q}{∆T}\)
\(C=\frac{4000}{70-20}\)
\(C=\frac{4000\ cal}{50}\)
\(C=80\ cal/°C\)
Por fim, calcularemos o valor do calor específico:
\(4000=500\cdot c\cdot 50\)
\(4000=25000\cdot c\)
\(\frac{4000}{25000}=c\)
\(0,16 \frac{cal}{g °C}=c\)
-
Questão 2
(Fuvest) Um amolador de facas, ao operar um esmeril, é atingido por fagulhas incandescentes, mas não se queima. Isso acontece porque as fagulhas:
A) têm calor específico muito grande.
B) têm temperatura muito baixa.
C) têm capacidade térmica muito pequena.
D) estão em mudança de estado.
E) não transportam energia.
Alternativa C
Isso acontece porque as fagulhas possuem uma massa muito pequena e, consequentemente, uma capacidade térmica baixa.
-
Questão 3
(Enem) Em um experimento foram utilizadas duas garrafas PET, uma pintada de branco e a outra de preto, acopladas cada uma a um termômetro. No ponto médio da distância entre as garrafas, foi mantida acesa, durante alguns minutos, uma lâmpada incandescente. Em seguida a lâmpada foi desligada. Durante o experimento, foram monitoradas as temperaturas das garrafas:
I. enquanto a lâmpada permaneceu acesa e
II. após a lâmpada ser desligada e ambas atingirem equilíbrio térmico com o ambiente.
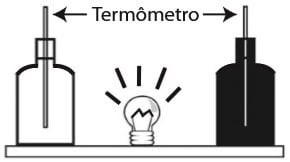
A taxa de variação da temperatura da garrafa preta, em comparação à da branca, durante todo o experimento, foi
A) igual no aquecimento e igual no resfriamento.
B) maior no aquecimento e igual no resfriamento.
C) menor no aquecimento e igual no resfriamento.
D) maior no aquecimento e menor no resfriamento.
E) maior no aquecimento e maior no resfriamento.
Alternativa E
A taxa de variação da temperatura da garrafa preta em comparação à da branca, durante todo o experimento, foi maior no aquecimento e maior no resfriamento, porque a garrafa preta tem a capacidade de absorver e de perder mais rapidamente a energia radiante do que a garrafa branca.
-
Questão 4
(PUC) Um líquido é aquecido por meio de uma fonte térmica que provê 50 cal por minuto. Observa-se que 200 g desse líquido se aquecem de 20,0 °C em 20,0 min. Qual é o calor específico do líquido, medido em cal/(g∙°C) ?
A) 0,0125
B) 0,25
C) 5,0
D) 2,5
E) 4,0
Alternativa B
Como a potência da fonte térmica é 50 cal/minutos, em 20 minutos o calor será de:
50 calorias → 1 minuto
Q calorias → 20 minutos
\(1\cdot Q=50\cdot20\)
Q = 1000 calorias fornecidas
Para encontrarmos o calor específico, basta usarmos a fórmula do calor sensível:
\(Q=m\cdot c\cdot∆T\)
\(1000=200\cdot c\cdot20\)
\(1000=4000\cdot c\)
\(\frac{1000}{4000}=c\)
\(0,25\ cal/g\cdot°C=c\)
-
Questão 5
Uma pessoa aquece um copo contendo 150 g de água, variando sua temperatura de 25 °C a 100 °C. Sabendo que o calor específico da água é de 1 cal/g∙°C, encontre a quantidade de calor recebido.
A) 11250 cal
B) 1125 cal
C) 1,125 cal
D) 11,250 cal
E) 112500 cal
Alternativa A
Como temos uma variação de temperatura sem mudança de estado físico, o calor, nesse caso, se trata do calor específico, e encontraremos seu valor por meio da fórmula:
\(Q=m\cdot c\cdot ∆T\)
\(Q=m\cdot c\cdot (T_f-T_i)\)
\(Q=150\cdot 1\cdot (100-25)\)
\(Q=150\cdot 1\cdot (75)\)
\(Q=11250\ cal\)
-
Questão 6
Um corpo sofre uma variação de temperatura de 100 °C quando é fonecido a ele 500 calorias de calor. Em vista disso, qual é a sua capacidade térmica?
A) 2 cal/°C
B) 3 cal/°C
C) 4 cal/°C
D) 5 cal/°C
E) 6 cal/°C
Alternativa D
A capacidade térmica desse corpo será encontrada por meio da fórmula que a relaciona ao calor e à temperatura:
\(C=\frac{Q}{∆T}\)
\(C=\frac{500}{100}\)
\(C=5\ cal/°C\)
-
Questão 7
Determine a quantidade de calor recebido por um líquido de 10 g que não variou sua temperatura, sabendo que seu calor latente é de 50 cal/g.
A) 370 cal
B) 160 cal
C) 280 cal
D) 420 cal
E) 500 cal
Alternativa E
Conforme informado, o líquido não variou sua temperatura, então temos um caso de calor latente. Encontraremos a quantidade de calor recebido por meio da fórmula do calor latente:
\(Q=m\cdot L\)
\(Q=10\cdot50\)
\(Q=500\ cal\)
-
Questão 8
Qual é a variação de comprimento de um fio metálico de prata, com coeficiente linear igual a \(10^{-5} °C^{-1}\), que sofre uma variação de temperatura de 250 °C, sabendo que seu comprimento inicial é de 600 m?
A) 2,5 m
B) 3 m
C) 3,5 m
D) 4 m
E) 4,5 m
Alternativa B
Para encontrarmos a variação de comprimento dilatada do fio metálico de prata, utilizaremos a fórmula da dilatação linear:
\(∆L=L_o\cdotα\cdot∆T\)
\(∆L=600\cdot2\cdot10^{-5}\cdot250\)
\(∆L=300000\cdot10^{-5}\)
\(∆L=3\cdot10^5\cdot10^{-5}\)
\(∆L=3\ m\)
-
Questão 9
Qual é a capacidade térmica de uma barra de chumbo com massa de 1,5 kg e calor específico de 0,0305 cal/g∙°C?
A) 0,4575 cal/°C
B) 4,575 cal/°C
C) 45,75 cal/°C
D) 457,5 cal/°C
E) 4575 cal/°C
Alternativa C
Primeiramente, vamos converter a massa de quilogramas para gramas:
\(1,5\ kg=1500\ g\)
De acordo com as informações dadas, é possível obter a capacidade térmica da barra de chumbo por meio da fórmula que a relaciona à massa e ao calor específico:
\(C=c\cdot m\)
\(C=0,0305\cdot1500\)
\(C=45,75\ cal/°C\)
-
Questão 10
Um cozinheiro esquece a sua concha dentro de uma panela com água que estava no fogo e quando a pega, ele acaba se queimando. Tempos depois, surge uma dúvida, e ele se pergunta quais foram as transmissões de calor que ocorreram na concha e na água dentro da panela, que são respectivamente:
A) condução e convecção.
B) condução e radiação.
C) convecção e radiação.
D) condução, convecção e radiação.
E) Não ocorreu transmissão de calor.
-
Questão 11
Determine a variação de área de uma chapa metálica de aço que variou sua temperatura de 15 °C para 70°C, sabendo que o seu coeficiente linear é igual a \(\mathbf{1,1\cdot10^{-5} °C^{-1}}\) e sua área inicial era de \(\mathbf{15\ m^2}\).
A) \(1374\cdot10^{-2} m^2\)
B) \(1,815\cdot10^{-2} m^2\)
C) \(1762\cdot10^{-3} m^2\)
D) \(1,925\cdot10^{-3} m^2\)
E) \(2,521\cdot10^{-4} m^2\)
Alternativa B
Para calcularmos a variação de área dilatada, utilizaremos a fórmula da dilatação superficial:
\(∆A=A_o\cdotβ\cdot∆T\)
Como não foi informado o valor do coeficiente de dilatação superficial, usaremos a sua relação com o coeficiente de dilatação linear:
\(∆A=A_o\cdot2\cdotα\cdot∆T\)
\(∆A=A_o\cdot2\cdotα\cdot(T_f-T_i)\)
\(∆A=15\cdot2\cdot1,1\cdot10^{-5}\cdot(70-15)\)
\(∆A=15\cdot2\cdot1,1\cdot10^{-5}\cdot(55)\)
\(∆A=1815\cdot10^{-5}\)
\(∆A=1,815\cdot10^3\cdot10^{-5}\)
\(∆A=1,815\cdot10^{3-5}\)
\(∆A=1,815\cdot10^{-2}\ m^2\)
-
Questão 12
Um corpo de massa 100 g recebeu 1250 cal quando variou sua temperatura de 30 °C até atingir 80 °C. Determine o seu calor específico.
A) 0,025 cal/g∙°C
B) 250 cal/g∙°C
C) 2,5 cal/g∙°C
D) 25 cal/g∙°C
E) 0,25 cal/g∙°C
Alternativa E
Para obtermos o calor específico, utilizaremos a fórmula que o relaciona ao calor, massa e temperatura:
\(c=\frac{Q}{m\cdot∆T}\)
\(c=\frac{Q}{m\cdot(T_f-T_i)}\)
\(c=\frac{1}{100\cdot(80-30)}\)
\(c=\frac{1250}{100\cdot(50)}\)
\(c=\frac{1250}{5000}\)
\(c=0,25\ cal/g\cdot°C\)