Exercícios sobre decomposição vetorial
Um vetor de tamanho 30 m faz um ângulo de 30º com a horizontal; com base nisso, calcule a componente horizontal e vertical desse vetor. Dados: \(sen 30°= 0,5\) e \(cos 30° = 0,9\) .
A) 18 m e 9 m
B) 20 m e 10 m
C) 22 m e 12 m
D) 25 m e 13 m
E) 27 m e 15 m
Alternativa E.
Como o ângulo está na horizontal, entre a componente horizontal e o vetor original, podemos calcular a componente horizontal por meio da fórmula:
\(F_{x} = F \cdot \cos \theta \)
\(F_{x} = 30 \cdot \cos 30^\circ \)
\(F_{x} = 30 \cdot 0,9 \)
\({F_x} = 27 m\)
E a componente vertical por meio da fórmula:
\(F_{y} = F \cdot \ sen \theta \)
\(F_{y} = 30 \cdot \ sen 30^\circ \)
\(F_{y} = 30 \cdot 0,5 \)
\(F_{y} = 15 \text{ m} \)
(PUC) A figura representa um bloco de massa m que, após ser lançado com velocidade v, sobe uma rampa de comprimento L, sem atrito, inclinada de um ângulo q.
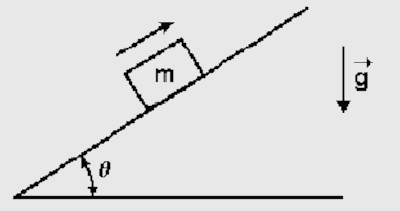
Assinale a opção que corresponde às forças que atuam no bloco enquanto ele estiver subindo a rampa.
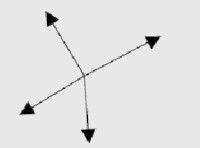
A) 
B) 
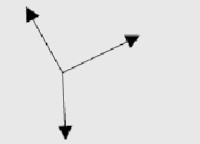
C) 
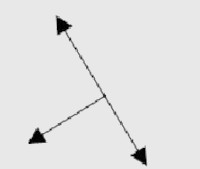
D) 
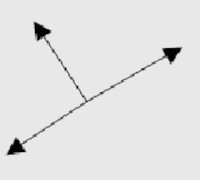
Alternativa C.
Neste exercício o bloco possui duas forças atuando: a força normal, perpendicular à superfície, e a força peso, apontando para baixo. Como elas não estão na mesma direção, teremos que decompor a força peso em uma componente horizontal x e uma componente vertical y. Como o vetor que representa a força peso está na diagonal esquerda (em relação à normal) apontando para baixo, a sua componente horizontal aponta para a esquerda. Já a componente vertical está apontando para baixo.
Em qual situação das alternativas abaixo não usamos a decomposição vetorial?
A) Identificar a componente horizontal de um vetor.
B) Calcular força no equilíbrio.
C) Identificar a componente vertical de um vetor.
D) Identificar o módulo, sentido e direção de grandezas escalares.
E) Verificar se as forças estão em equilíbrio.
Alternativa D.
Quando temos grandezas escalares não usamos a decomposição vetorial, já que elas não possuem direção e sentido.
Sabendo que um vetor na diagonal direita tem sentido para baixo, qual o sentido da sua componente horizontal e componente vertical?
A) Componente horizontal para a direita e componente vertical para cima
B)Componente horizontalpara a esquerda e componente vertical para cima
C) Componente horizontal para a direita e componente vertical para baixo
D) Componente horizontal para a esquerda e componente vertical para baixo
E) Nesse caso não temos componentes horizontal e vertical
Alternativa C.
Quando temos um vetor na diagonal para a direita apontando para baixo, a sua componente horizontal fica acima dele, ou seja, na horizontal apontando para a direita. Já a componente vertical fica ao lado esquerdo dele, ou seja, na vertical apontando para baixo.
Uma pessoa realiza uma força F de 100 N para levantar uma caixa no solo. Considerando que a força foi aplicada com a angulação descrita na imagem abaixo, calcule o módulo das componentes horizontal e vertical. Dados: \(sen 30° = 0,5\) e \(cos 30° = 0,9\).
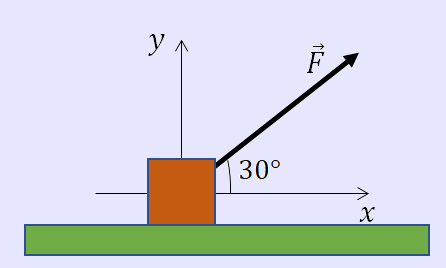
A) 90 N e 50 N
B) 100 N e 60 N
C) 110 N e 70 N
D) 120 N e 80 N
E) 130 N e 90 N
Alternativa A.
Primeiramente, calcularemos o módulo da componente horizontal da força F, por meio da fórmula:
\(F_{x} = F \cdot \cos \theta \)
\(F_{x} = 100 \cdot \cos 30^\circ \)
\(F_{x} = 100 \cdot 0,9 \)
\({F_x} = 90 N\)
Depois, calcularemos o módulo da componente vertical da força F, por meio da fórmula:
\(F_{y} = F \cdot \ sen \theta \)
\(F_{y} = 100 \cdot \ sen 30^\circ \)
\(F_{y} = 100 \cdot 0,5 \)
\({F_y} = 50 N\)
Após seus estudos a respeito da decomposição vetorial, responda: quais dos tipos de grandezas abaixo podem ser decompostas vetorialmente?
A) Grandezas escalares.
B) Grandezas escalares na direção diagonal.
C) Grandezas escalares na direção horizontal.
D) Grandezas vetoriais.
Alternativa D.
As grandezas escalares não podem ser decompostas vetorialmente, já que não são representadas por um vetor. Somente as grandezas vetoriais podem ser decompostas vetorialmente, já que são representadas por um vetor com direção, módulo e sentido.
Um vetor \(\vec{V} \) está apontado na diagonal esquerda para cima; suas componentes \({V_x}\) e \({V_y}\) estão localizadas aonde?
A) \({V_x}\) na horizontal para a direita e \({V_y}\) na vertical para cima
B) \({V_x}\) na horizontal para a esquerda e \({V_y}\) na vertical para cima
C) \({V_x}\) na horizontal para a direita e \({V_y}\) na vertical para baixo
D) \({V_x}\) na horizontal para a esquerda e \({V_y}\) na vertical para baixo
E) Nesse caso não temos componentes horizontal e vertical
Alternativa B.
Quando temos um vetor na diagonal para a esquerda apontando para cima, a sua componente horizontal fica abaixo dele, ou seja, na horizontal apontando para a esquerda. Já a componente vertical fica ao lado direito dele, ou seja, na vertical apontando para cima.
Calcule o módulo da componente horizontal das forças \(\vec{\mathbf{F}}_{1} \) e \(\vec{\mathbf{F}}_{2}\) de intensidade igual a 50 N, conforme descritas na imagem abaixo. Considere \(sen 10° = 0,17\), \(cos 10° = 0,98\), \(sen 50° = 0,76\) e \(cos 50° = 0,64\).
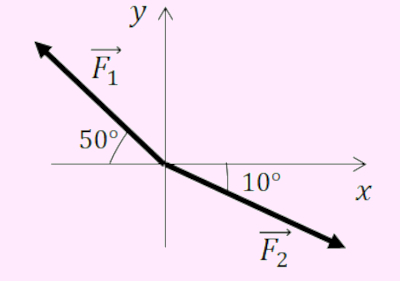
A) 25N e 41N
B) 26N e 43N
C) 28N e 45N
D) 30N e 47N
E) 32N e 49N
Alternativa E.
Primeiramente, calcularemos o módulo da componente horizontal da força \({F_1}\), por meio da fórmula:
\(F_{1x} = F_{1} \cdot \cos \theta \)
\(F_{1x} = 50 \cdot \cos 50^\circ \)
\(F_{1x} = 50 \cdot 0,64 \)
\(F_{1x} = 32 \text{ N} \)
Depois, calcularemos o módulo da componente horizontal da força \({F_2}\), por meio da fórmula:
\(F_{2x} = F_{2} \cdot \cos \theta \)
\(F_{2x} = 50 \cdot \cos 10^\circ \)
\(F_{2x} = 50 \cdot 0,98 \)
\(F_{2x} = 49 \text{ N} \)
Para decompor vetorialmente as grandezas físicas, é necessário identificar se elas são grandezas escalares ou grandezas vetoriais. Pensando nisso, qual das grandezas físicas abaixo é uma grandeza vetorial?
A) Condutividade
B) Tempo
C) Força
D) Energia
E) Resistência
Alternativa C.
A força é uma grandeza física vetorial, já que ela é descrita em termos de um módulo, direção e sentido. Em razão disso, ela pode ser decomposta vetorialmente em uma componente horizontal e uma componente vertical.
Uma criança aplica uma força de 40N em um trenó, formando um ângulo de 20º com a horizontal. Com base nessas informações, calcule a componente horizontal e vertical, respectivamente. Considere \(sen 20° =0,3\) e \(cos 20° =0,9\).
A) 32N e 9N
B) 36N e 12N
C) 40N e 15N
D) 44N e 18N
E) 48N e 21N
Alternativa B.
Primeiramente, calcularemos o módulo da componente horizontal da força F, por meio da fórmula:
\(F_{x} = F \cdot \cos \theta \)
\(F_{x} = 40 \cdot \cos 20^\circ \)
\(F_{x} = 40 \cdot 0,9 \)
\({F_x} = 36 N\)
Depois, calcularemos o módulo da componente vertical da força F, por meio da fórmula:
\(F_{y} = F \cdot \ sen \theta \)
\(F_{y} = 40 \cdot \ sen 20^\circ \)
\(F_{y} = 40 \cdot 0,3 \)
\(F_{y} = 12 \text{ N} \)
Um vetor \(\vec {Z}\) está apontado na diagonal direita para cima, então as suas componentes \({Z_x}\) e \({Z_y}\) estão apontadas para onde?
A) \({Z_x}\) na horizontal para a direita e \({Z_y}\) na vertical para cima
B) \({Z_x}\) na horizontal para a esquerda e \({Z_y}\) na vertical para cima
C) \({Z_x}\) na horizontal para a direita e \({Z_y}\) na vertical para baixo
D) \({Z_x}\) na horizontal para a esquerda e \({Z_y}\) na vertical para baixo
E) Nesse caso não temos componentes horizontal e vertical
Alternativa A.
Quando temos um vetor na diagonal para a direita apontando para cima, a sua componente horizontal fica abaixo dele, ou seja, na horizontal apontando para a direita. Já a componente vertical fica ao lado esquerdo dele, ou seja, na vertical apontando para cima.
Um vetor \(\vec {A}\) tem componente vertical de tamanho 12 unidades e componente horizontal de tamanho 16 unidades. Sabendo que esse vetor faz um ângulo de 60º com o eixo y, calcule o tamanho do vetor A.
A) 12 unidades
B) 24 unidades
C) 6 unidades
D) 18 unidades
E) 32 unidades
Alternativa B.
Calcularemos o tamanho do vetor \(\vec {A}\) por meio da fórmula que relaciona a componente vertical com o vetor e o cosseno do ângulo formado entre o vetor original e a vertical:
\(A_{y} = A \cdot \cos \theta \)
\(12 = A \cdot \cos 60^\circ \)
\(12= A \cdot 0,5\)
\(A = \frac{12}{0,5} \)
\(A=24 \ unidades\)
