Exercícios sobre elevadores
Estes exercícios sobre elevadores abordam as marcações de peso aparente na subida e descida em movimento acelerado.
Publicado por: Joab Silas da Silva JúniorQuestões
-
Questão 1
Em um elevador há um homem de massa igual a 95 kg sobre uma balança graduada em newton. Em um instante, o elevador começa a subir com aceleração de 0,5 m/s2. Determine a diferença percentual aproximada entre a marcação do peso do homem no elevador em repouso e em movimento.
Dado: g = 10 m/s2
a) 7,8 %
b) 5,8 %
c) 4,8 %
d) 2,8 %
e) 9,8 %
LETRA “C”
No momento em que o elevador está parado, a marcação da balança, que representa a força normal, é igual à força peso, logo:
P = N
m. g = N
N = 95. 10 = 950 N
No momento em que o elevador inicia a subida, a força resultante será dada pela diferença entre a força normal e o peso, logo:
FR = m.a
N – P = m.a
N = m.a + mg
N = m.(a + g)
N = 95.(0,5 + 10)
N = 997,5 N
A diferença percentual entre as marcações é: Dp = (997,5 – 950) x 100 = 4,76% 997,5
-
Questão 2
Determine o peso aparente de uma pessoa de massa igual a 50 kg que está em um elevador que desce com aceleração igual a 1 m/s2.
Dado: g = 10 m/s2
a) 460 kg
b) 458 kg
c) 455 kg
d) 445 kg
e) 450 kg
LETRA “E”
Na descida do elevador, a força resultante é dada pela diferença entre a força peso e a força normal:
FR = m.a
P – N = m.a
N = m.g – m.a
N = m (g – a)
N = 50 (10 – 1)
N = 450 N
A marcação indicada por uma balança corresponde à força normal. Nesse caso, a indicação é menor que o peso real da pessoa, que é de 500N.
-
Questão 3
(Unifor-CE) Um corpo de massa 2,0 kg está pendurado em um dinamômetro preso ao teto de um elevador. Uma pessoa no interior deste elevador observa que a indicação fornecida pelo dinamômetro é 26N. Considerando a aceleração local da gravidade de 10 m/s2, o elevador pode estar:
a) em repouso.
b) descendo com aceleração de 2,0 m/s2
c) descendo em movimento uniforme
d) subindo com velocidade constante
e) subindo com aceleração de 3,0 m/s2
LETRA “E”
O peso aparente de um corpo que está dentro de um elevador em movimento acelerado será maior que o peso real somente se o elevador estiver subindo. Nesse caso, a força resultante do sistema será a diferença entre a força normal e a força peso.
FR = m.a
N – P = m.a
N = m.a + m.g
N = m. (a + g)
26 = 2 (a + 10)
(a + 10) = 13
a = 3,0 m/s2
-
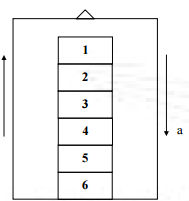
Questão 4
(ITA) Uma pilha de seis blocos iguais, de mesma massa m, repousa sobre o piso de um elevador, como mostra a figura. O elevador está subindo em movimento uniformemente retardado com uma aceleração de módulo a. O módulo da força que o bloco 3 exerce sobre o bloco 2 é dado por
a) 3m (g + a)
b) 3m (g – a)
c) 2m (g + a)
d) 2m (g – a)
e) m (2g – a)
LETRA “B”
A força exercida pelo bloco 3 sobre o bloco 2 é a força normal referente ao peso dos blocos 1 e 2. Nesse caso, a força resultante é dada pela diferença do peso pela força normal, portanto:
FR = 2m.a
P – N = 2m.a
N = 2m.g – 2m.a
N = 2m (g – a)