Exercícios sobre energia cinética
(Fatec) Um motorista conduzia seu automóvel de massa 2000 kg que trafegava em linha reta, com velocidade constante de 72 km/h, quando avistou uma carreta atravessada na pista. Transcorreu 1 s entre o momento em que o motorista avistou a carreta e o momento em que acionou o sistema de freios para iniciar a frenagem, com desaceleração constante igual a 10 m/s2 . Desprezando-se a massa do motorista, assinale a alternativa que apresenta, em Joules, a variação da energia cinética desse automóvel, do início da frenagem até o momento de sua parada.
A) \(+\ 4,0\cdot{10}^5\)
B) \(+\ 3,0\cdot{10}^5\)
C) \(+\ 0,5\cdot{10}^5\)
D) \(-\ 4,0\cdot{10}^5\)
E) \(-\ 2,0\cdot{10}^5\)
Alternativa D
Primeiramente, converteremos a velocidade inicial de km/h para m/s:
\(\frac{72\ km/h}{3,6}=20\ m/s\)
Para encontrar a energia cinética inicial, usaremos a fórmula:
\(E_{c\ inicial}=\frac{m\cdot v^2}{2}\)
\(E_{c\ inicial}=\frac{2000\cdot{20}^2}{2}\)
\(E_{c\ inicial}=\frac{2000\cdot400}{2}\)
\(E_{c\ inicial}=\frac{800000}{2}\)
\(E_{c\ inicial}=400000\)
\(E_{c\ inicial}=4,0\cdot{10}^5\ J\)
A energia cinética final será zero, já que a velocidade do automóvel diminuirá até parar. Então, a variação de energia cinética é:
\(∆E_{c\ }=E_{c\ } final-E_{c\ } inicial\)
\(∆E_{c\ }=0-4,0\cdot{10}^5\ \)
\(∆E_{c\ }=0-4,0\cdot{10}^5\ J\)
(ITA) Um projétil de massa m = 5,00 g atinge perpendicularmente uma parede com velocidade do módulo V = 400 m/s e penetra 10,0 cm na direção do movimento. (Considere constante a desaceleração do projétil na parede e admita que a intensidade da força aplicada pela parede não depende de V).
A) Se V = 600m/s, a penetração seria de 15,0 cm.
B) Se V = 600m/s, a penetração seria de 225,0 cm.
C) Se V = 600m/s, a penetração seria de 22,5 cm.
D) Se V = 600m/s, a penetração seria de 150 cm.
E) A intensidade da força imposta pela parede à penetração da bala é 2,00 N.
Alternativa C
De início, vamos converter a massa de gramas para quilogramas, sendo 5 g=0,005 kg, e a distância de centímetros para metros, sendo 10 cm=0,1 m .
Para analisarmos qual das alternativas está correta, usaremos o teorema do trabalho e energia cinética:
\(\tau=∆E_{c\ }\)
\(\tau=E_{c\ final}-E_{c\ inicial}\)
\(\tau=0-\frac{m\cdot v^2}{2}\)
\(\tau=0-\frac{0,005\cdot{400}^2}{2}\)
\(\tau=0-\frac{0,005\cdot160000}{2}\)
\(\tau=-\ 400\ J\)
Agora, encontraremos o valor da força de resistência:
\(\tau=F\cdot d\)
\(400=F\cdot0,1\)
\(F=\frac{400}{0,1}\)
\(F=\frac{400}{0,1}\)
\(F=4000\ N\)
Por fim, para uma velocidade de 600 m/s, a distância será:
\(\tau=E_c\)
\(F\cdot d=\frac{m\cdot v^2}{2}\)
\(4000\cdot d=\ \frac{0,005\cdot{600}^2}{2}\)
\(d=0,225\ m\ \)
\(d=22,5\ cm\ \)
(FGV) Em alguns países da Europa, os radares fotográficos das rodovias, além de detectarem a velocidade instantânea dos veículos, são capazes de determinar a velocidade média desenvolvida pelos veículos entre dois radares consecutivos. Considere dois desses radares instalados em uma rodovia retilínea e horizontal. A velocidade instantânea de certo automóvel, de 1500 kg de massa, registrada pelo primeiro radar foi de 72 km/h. Um minuto depois, o radar seguinte acusou 90 km/h para o mesmo automóvel.
O trabalho realizado pela resultante das forças agentes sobre o automóvel foi, em Joules, mais próximo de
A) \(1,5\cdot{10}^4\)
B) \(5,2\cdot{10}^4\)
C) \(7,5\cdot{10}^4\)
D) \(1,7\cdot{10}^5\)
E) \(3,2\cdot{10}^5\)
Alternativa D
Inicialmente, converteremos a velocidade inicial e final de km/h para m/s:
\(v_{final}=\frac{90\ km/h}{3,6}=25\ m/s\)
\(v_{inicial}=\frac{72\ km/h}{3,6}=20\ m/s\)
Então, usaremos o teorema do trabalho e energia cinética:
\(∆\tau=E_{c\ }\)
\(\tau=E_{c\ final}-E_{c\ inicial}\)
\(\tau=\frac{m\cdot{v_{final}}^2}{2}-\frac{m\cdot{v_{inicial}}^2}{2}\)
\(\tau=\frac{1500\cdot{25}^2}{2}-\frac{1500\cdot{20}^2}{2}\)
\(\tau=\frac{1500\cdot625}{2}-\frac{1500\cdot400}{2}\)
\(\tau=468750-300000\)
\(\tau=168750\ \)
\(\tau=1,68750\cdot{10}^5\ J\)
(PUC) Sabendo que um corredor cibernético de 80 kg, partindo do repouso, realiza a prova de 200 m em 20 s mantendo uma aceleração constante de a = 1,0 m/s², pode-se afirmar que a energia cinética atingida pelo corredor no final dos 200 m, em Joules, é:
A) 12000
B) 13000
C) 14000
D) 15000
E) 16000
Alternativa E
Primeiramente, encontraremos o valor da velocidade final por meio da equação de Torricelli:
\(v_f^2=v_0^2+2\cdot a\cdot∆x\)
\(v_f^2=0^2+2\cdot1\cdot200\)
\(v_f^2=0+400\)
\(v_f^2=400\)
\(v_f=\sqrt{400}\)
\(v_f=20\ m/s\)
Por fim, calcularemos a energia cinética por meio da sua fórmula:
\(E_c=\frac{m\cdot v^2}{2}\)
\(E_c=\frac{80\cdot{20}^2}{2}\)
\(E_c=\frac{80\cdot400}{2}\)
\(E_c=16000\ J\)
Qual a energia cinética de um carro com massa de 1200 kg que se move com velocidade de 50 m/s?
A) \(1,5\cdot{10}^5\ J\)
B) \(1,5\cdot{10}^6\ J\)
C) \(1,5\cdot{10}^7\ J\)
D) \(1,5\cdot{10}^8\ J\)
E) \(1,5\cdot{10}^9\ J\)
Alternativa B
Encontraremos o valor da energia cinética por meio da sua fórmula:
\(E_c=\frac{m\cdot v^2}{2}\)
\(E_c=\frac{1200\cdot{50}^2}{2}\)
\(E_c=\frac{1200\cdot2500}{2}\)
\(E_c=1500000 \)
\(E_c=1,5\cdot{10}^6\ J\)
Qual é o trabalho realizado por uma pessoa de 70 kg que aumenta sua velocidade de 4/s m para 16 m/s?
A) 8400 J
B) 8960 J
C) 140 J
D) 560 J
E) 0 J
Alternativa A
Para encontrarmos o valor, usaremos o teorema do trabalho e energia cinética:
\(\tau=∆E_{c\ }\)
\(\tau=E_{c\ final}-E_{c\ inicial}\)
\(\tau=\frac{m\cdot{v_{final}}^2}{2}-\frac{m\cdot{v_{inicial}}^2}{2}\)
\(\tau=\frac{70\cdot{16}^2}{2}-\frac{70\cdot4^2}{2}\)
\(\tau=\frac{70\cdot256}{2}-\frac{70\cdot16}{2}\)
\(\tau=8960-560\)
\(\tau=8400\ J\)
Um atleta de salto em vara corre a uma velocidade de 10 m/s antes de firmar a vara no chão e subir. Se ele conseguir converter 70% de sua energia cinética em energia potencial gravitacional, qual será a altura máxima que ele conseguirá atingir? Considere a aceleração da gravidade como sendo 10 ms2.
A) 9,2 metros
B) 1,0 metros
C) 4,8 metros
D) 7,6 metros
E) 3,5 metros
Alternativa E
Usaremos o teorema da conservação de energia mecânica para encontrarmos o valor da altura máxima:
\(E_{m\ antes}=E_{m\ depois}\)
A energia mecânica é a soma entre a energia cinética e a energia potencial, portanto:
\(E_{c\ antes}+E_{p\ antes}=E_{c\ depois}+E_{p\ depois}\)
A energia potencial é a soma entre a energia potencial elástica e a energia potencial gravitacional, então:
\({E_{c\ antes}+E}_{pel\ antes}+E_{pg\ antes}=E_{c\ depois}+E_{pel\ depois}+E_{pg\ depois}\)
Como antes do salto ele adquiriu velocidade, então temos energia cinética, mas ele não teve uma variação de altura, portando desconsideraremos a energia potencial gravitacional antes.
Já após o salto, a velocidade diminuiu consideravelmente até atingir zero, então desconsideraremos a energia cinética. Mas como houve variação de altura, há energia potencial gravitacional. Desconsideraremos a energia potencial elástica, já que não estamos trabalhando com molas.
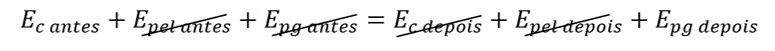
\(E_{c\ antes}=E_{pg\ depois}\)
Como ele conseguiu converter 70% da sua energia cinética em energia potencial, temos:
70% ∙ Ec antes=Epg depois
\(\frac{70}{100}\cdot\frac{m\cdot v^2}{2}=m\cdot g\cdot h\)
\(\frac{70}{100}\cdot\frac{{10}^2}{2}=10\cdot h\)
\(\frac{70}{100}\cdot\frac{100}{2}=10\cdot h\)
\(\frac{7000}{200}=10\cdot h\)
\(35=10\cdot h\)
\(\frac{35}{10}=h\)
\(3,5\ m=h\)
Um cachorro com massa de 10 kg está dentro de um carro que se movimenta com velocidade de 180 km/h. Determine a sua energia cinética.
A) 125 J
B) 12500 J
C) 125000 J
D) 1250 J
E) 1250000 J
Alternativa B
De início, converteremos a velocidade de km/h para m/s:
\(v_{final}=\frac{180\ km/h}{3,6}=50\ m/s\)
Agora, podemos encontrar a energia cinética do cachorro por meio da fórmula da energia cinética:
\(E_{c\ }=\frac{m\cdot v^2}{2}\)
\(E_{c\ }=\frac{10\cdot{50}^2}{2}\)
\(E_{c\ }=\frac{10\cdot2500}{2}\)
\(E_{c\ }=12500\ J\)
Uma pessoa observa dois carros, A e B, ambos com massas de 1500 kg, que se movem com velocidades constantes de 100 km/h e 140 km/h, respectivamente. Considerando essas informações, determine a razão aproximada entre as energias cinéticas desses carros \(\frac{E_{c\ A}}{E_{c\ B}}\):
A) 0,930
B) 0,720
C) 0,510
D) 0,308
E) 0,104
Alternativa C
Inicialmente, encontraremos a energia cinética do carro A:
\(E_{c\ A}=\frac{m\cdot v^2}{2}\)
\(E_{c\ A}=\frac{1500\cdot{100}^2}{2}\)
\(E_{c\ A}=\frac{1500\cdot10000}{2}\)
\(E_{c\ A}=7500000\ \)
\(E_{c\ A}=7,5\cdot{10}^6\ J\)
Já a energia cinética do carro B é:
\(E_{c\ B}=\frac{m\cdot v^2}{2}\)
\(E_{c\ B}=\frac{1500\cdot{140}^2}{2}\)
\(E_{c\ B}=\frac{1500\cdot19600}{2}\)
\(E_{c\ B}=14700000\ \)
\(E_{c\ B}=14,7\cdot{10}^6\ J\ \)
Portanto, a relação entre as energias cinéticas de A e B é:
\(\frac{E_{c\ A}}{E_{c\ B}}=\frac{7,5\cdot{10}^6}{14,7\cdot{10}^6}\ \)
\(\frac{E_{c\ A}}{E_{c\ B}}=\frac{7,5}{14,7}\ \)
\(\frac{E_{c\ A}}{E_{c\ B}}\approx0,510\ \)
Podemos utilizar a energia cinética para encontrar diversas informações, exceto:
A) a altura de queda de um corpo.
B) fazer análises astronômicas.
C) estudar o movimento de partículas altamente energéticas.
D) o trabalho realizado sobre um corpo.
E) a velocidade dos corpos.
Alternativa A
Por meio da energia cinética conseguimos fazer análises astronômicas, estudar o movimento de partículas altamente energéticas, encontrar o trabalho realizado sobre um corpo, além da velocidade dos corpos. Entretanto, para encontrarmos a altura de queda de um corpo, é necessário calcularmos a energia potencial gravitacional.
Lembrando dos seus estudos a respeito da energia cinética, assinale a alternativa abaixo que corresponde à sua fórmula relativística:
A) \(E_c=\frac{m\cdot v^2}{2}\)
B) \(E_c=\left(\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\right)m\cdot c^2\)
C) \(E_c=m\cdot g\cdot h\)
D) \(E_c=\frac{k\ \cdot{\ x}^2}{2}\)
E) \(E_c=F\cdot d\)
Alternativa B
A fórmula usada para calcular a energia cinética relativística é:
\(E_c=\left(\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\right)m\cdot c^2\)
Em relação às outras alternativas:
\(E_c=\frac{m\cdot v^2}{2}\) é a fórmula da energia cinética.
\(E_c=m\cdot g\cdot h\) é a fórmula da energia potencial gravitacional.
\(E_c=\frac{k\ \cdot{\ x}^2}{2}\) é a fórmula da energia potencial elástica.
\(E_c=F\cdot d \) é a fórmula da relação da energia cinética com o trabalho.
A respeito da energia cinética, quais das proposições informam corretamente a relação entre a grandeza física e a sua unidade de medida?
I. A energia cinética é medida em Newton.
II. A energia potencial é medida em Joule.
III. A velocidade é medida em metros por segundo ao quadrado.
IV. A massa é medida em quilograma.
V. O trabalho é medido em Joule.
A) Alternativas I e II.
B) Alternativas III e IV
C) Alternativas I, III e V.
D) Alternativas II, IV e V.
E) Nenhuma alternativa.
Alternativa D
I. A energia cinética é medida em Newton. (Falso)
A energia cinética é medida em Joule.
II. A energia potencial é medida em Joule. (Verdadeiro)
III. A velocidade é medida em metros por segundo ao quadrado. (Falso)
A velocidade é medida em metros por segundo.
IV. A massa é medida em quilograma. (Verdadeiro)
V. O trabalho é medido em Joule. (Verdadeiro)
