Exercícios sobre energia potencial gravitacional
(Fuvest — adaptada) No rótulo de uma lata de leite em pó lê-se “valor energético: 1509 kJ por 100 g (361 kcal)”. Se toda energia armazenada em uma lata contendo 400 g de leite fosse utilizada para levantar um objeto de 10 kg, a altura máxima atingida seria de aproximadamente (g = 10 m/s²):
A) h = 50,37 km
B) h = 71,36 km
C) h = 61,37 km
D) h = 60,36 km
E) h = 70,36 km
Alternativa D.
Primeiramente, encontraremos o valor energético de 400 gramas de leite, através de uma regra de três simples:
100 gramas−1509 KJ
400 gramas–x
x⋅100=1509⋅400
x=603600100
x=6036 kJ
x=6036⋅103 J
Então, calcularemos a altura máxima atingida para levantar a lata, através da fórmula da energia potencial gravitacional:
Epg=m⋅g⋅h
6036⋅103=10⋅10⋅h
6036⋅103=100⋅h
h=6036⋅103100
h=6036⋅1000100
h=60360 m
(Anhembi Morumbi) Considere um ônibus espacial, de massa aproximada 1,0⋅105 kg, que, dois minutos após ser lançado, atingiu a velocidade de 1,34⋅103 m/s e a altura de 4,5⋅104 m. Sabendo que a aceleração gravitacional terrestre vale 10 m/s², é correto afirmar que, naquele momento, as energias cinética e potencial, aproximadas, em joules, desse ônibus espacial, em relação ao solo, eram, respectivamente,
A) 3,0⋅1010 e 9,0⋅1010
B) 9,0⋅1010 e 4,5⋅1010
C) 9,0⋅1010 e 3,0⋅1010
D) 3,0⋅1010 e 4,5⋅1010
E) 4,5⋅1010 e 3,0⋅1010
Alternativa B.
Primeiramente, calcularemos a energia cinética do ônibus espacial, através da sua fórmula:
Ec=m⋅v22
Ec=1,0⋅105⋅(1,34⋅103)22
Ec=1,0⋅105⋅1,7956⋅1062
Ec=0,8978⋅105+6
Ec=0,8978⋅1011
Ec=8,978⋅10−1⋅1011
Ec=8,978⋅10−1+11
Ec=8,978⋅1010 J
Ec≅9,0⋅1010 J
Depois, calcularemos a energia potencial gravitacional do ônibus espacial, através da sua fórmula:
Epg=m⋅g⋅h
Epg=1,0⋅105⋅10⋅4,5⋅104
Epg=45⋅105+4
Epg=45⋅109
Epg=4,5⋅101⋅109
Epg=4,5⋅101+9
Epg=4,5⋅1010 J
(UCB) Determinado atleta usa 25% da energia cinética obtida na corrida para realizar um salto em altura sem vara. Se ele atingiu a velocidade de 10 m/s, considerando g = 10 m/s², a altura atingida em razão da conversão de energia cinética em potencial gravitacional é a seguinte:
A) 1,12 m.
B) 1,25 m.
C) 2,5 m.
D) 3,75 m.
E) 5 m.
Alternativa B.
Calcularemos a altura atingida através da conversão da energia cinética em energia potencial gravitacional, dada pela igualdade das energias:
25% Ec=Epg
25100⋅m⋅v22=m⋅g⋅h
25100⋅1022=10⋅h
25100⋅1002=10⋅h
12,5=10⋅h
h=12,510
h=1,25 m
A respeito dos tipos de energia potencial, marque a alternativa incorreta:
a) A energia potencial gravitacional é armazenada em virtude da posição ocupada por um objeto qualquer.
b) A constante elástica de uma mola indica se ela é de fácil ou difícil deformação.
c) A energia potencial elástica é a metade do produto da constante elástica pela deformação sofrida pela mola.
d) A energia potencial elástica é armazenada em um material elástico em virtude de sua deformação.
e) Relacionar o conceito de energia somente à ideia de movimento é um erro, uma vez que, ao ocupar uma posição, um corpo possui energia potencial armazenada.
LETRA “C”
A energia potencial elástica é definida como a metade do produto da constante elástica pela deformação da mola elevada ao quadrado.
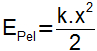
(Fatec) Um bloco de massa 0,60 kg é abandonado, a partir do repouso, no ponto A de uma pista no plano vertical. O ponto A está a 2,0 m de altura da base da pista, onde está fixa uma mola de constante elástica 150 N/m. São desprezíveis os efeitos do atrito, e adota-se g = 10m/s². A máxima compressão da mola vale, em metros:
A) 0,80
B) 0,40
C) 0,20
D) 0,10
E) 0,05
Alternativa B.
Calcularemos a compressão máxima da mola através da conversão da energia potencial gravitacional em energia potencial elástica, dada pela igualdade das energias:
Epg=Eel
m⋅g⋅h=k⋅x22
0,6⋅10⋅2=150⋅x22
12=75⋅x2
x2=1275
x2=0,16
x=√0,16
x=0,4 m
Uma caixa de 20 kg cai de uma altura de 3 metros. Sabendo que a aceleração da gravidade é de aproximadamente 10 m/s2, calcule a sua energia potencial gravitacional.
A) 200 J
B) 300 J
C) 400 J
D) 500 J
E) 600 J
Alternativa E.
Calcularemos a energia potencial gravitacional através da sua fórmula:
Epg=m⋅g⋅h
Epg=20⋅10⋅3
Epg=600 J
Qual a energia potencial gravitacional sofrida por um corpo de 100 kg que está a uma altura de 20 metros do solo, em um planeta com aceleração da gravidade de 4 m/s²?
A) 8 000 J
B) 10 000 J
C) 12 000 J
D) 14 000 J
E) 16 000 J
Alternativa A.
Calcularemos a energia potencial gravitacional através da sua fórmula:
Epg=m⋅g⋅h
Epg=100⋅4⋅20
Epg=8 000 J
Determine a altura máxima atingida por um atleta de salto com vara que corre 10 m/s antes de firmar a vara no chão e pular, sendo que ele consegue converter 50% da sua energia cinética em energia potencial gravitacional. Considere a aceleração da gravidade como 10 m/s2.
A) 1,4 metros
B) 3,1 metros
C) 5,8 metros
D) 4,9 metros
E) 2,5 metros
Alternativa E.
Calcularemos a altura máxima atingida pelo atleta através da conversão da energia cinética em energia potencial gravitacional, dada pela igualdade das energias:
50% Ec=Epg
50100⋅m⋅v22=m⋅g⋅h
0,5⋅1022=10⋅h
0,5⋅1002=10⋅h
25=10⋅h
h=2510
h=2,5 m
Qual a altura de um objeto de massa 5 kg que cai de um avião com energia potencial gravitacional de 20.000 J? Considere a aceleração da gravidade como 10 m/s2.
A) 100 m
B) 200 m
C) 300 m
D) 400 m
E) 500 m
Alternativa D.
Calcuremos a altura do objeto através da fórmula da energia potencial gravitacional:
Epg=m⋅g⋅h
20 000=5⋅10⋅h
20 000=50⋅h
h=20 00050
h=400 m
Quanto vale a relação entre as energias potenciais gravitacionais Epg P/Epg R de uma pena de 100 g e uma rocha de 500 g que caem de uma altura de 1,5 metros? Considere a aceleração da gravidade como 10 m/s2.
A) 0,2
B) 0,4
C) 0,8
D) 1,6
E) 3,2
Alternativa A.
Primeiramente, converteremos as massas de gramas para quilogramas:
100g=0,1 kg
500 g=0,5 kg
Depois, encontraremos a relação entre as energias potenciais gravitacionais da pena e da rocha, através da fórmula da energia potencial gravitacional:
Epg PEpg R=mP⋅g⋅hPmR⋅g⋅hR
Epg PEpg R=0,1⋅10⋅1,50,5⋅10⋅1,5
Epg PEpg R=1,57,5
Epg PEpg R=0,2
A energia potencial gravitacional pode ser usada para encontrar diversas informações, com exceção de:
A) massa do corpo.
B) energia cinética do corpo.
C) análises microscópicas.
D) altura do corpo.
E) energia potencial elástica do corpo.
Alternativa C.
A energia potencial gravitacional pode ser usada para encontrar a massa e altura dos corpos através da sua fórmula. Também pode ser usada para encontrar a energia cinética e energia potencial elástica dos corpos através da conservação da energia mecânica. Porém, não é usada para análises microscópicas.
Com base em seus estudos a respeito da energia potencial gravitacional, marque qual alternativa abaixo corresponde à sua fórmula:
A) Epg=m⋅c2√1−v2c2
B) Epg=m⋅v22
C) Epg=m⋅g⋅h
D) Epg=F⋅d
E) Epg=k⋅x22
Alternativa C.
A fórmula usada para calcular a energia potencial gravitacional é:
Epg=m⋅g⋅h
Já as outras alternativas correspondem a:
A) energia cinética relativística.
B) energia cinética.
D) trabalho.
E) energia potencial elástica.
A respeito da energia potencial gravitacional, quais das proposições informam corretamente a relação entre a grandeza física e a sua unidade de medida?
I. A energia potencial gravitacional é medida em Joule.
II. A energia cinética é medida em Joule.
III. A aceleração da gravidade é medida em segundo ao quadrado.
IV. A massa é medida em Joule.
V. A altura é medida em quilograma.
Qual das alternativas abaixo está correta?
A) Apenas I e II.
B) Alternativas III e IV
C) Alternativas I, III e V.
D) Alternativas II, IV e V.
E) Nenhuma alternativa.
Alternativa A.
I. A energia potencial gravitacional é medida em Joule. (verdadeiro)
II. A energia cinética é medida em Joule. (verdadeiro)
III. A aceleração da gravidade é medida em segundo ao quadrado. (falso)
A aceleração da gravidade é medida em metros por segundo ao quadrado.
IV. A massa é medida em Joule. (falso)
A massa é medida em quilograma.
V. A altura é medida em quilograma. (falso)
A altura é medida em metros.






