Exercícios sobre estática
(Encceja) A imagem representa uma balança utilizada para a medida da massa de uma fruta. A massa colocada no prato direito da balança é de 100 g e o sistema encontra-se em equilíbrio.
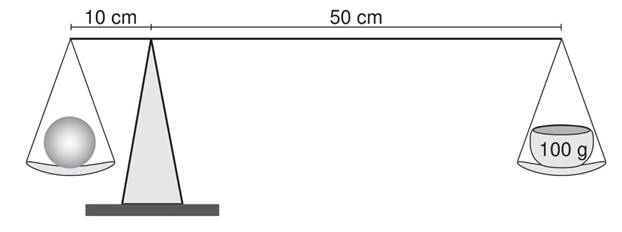
A massa dessa fruta, em grama, é:
A) 100
B) 120
C) 500
D) 600
Alternativa C
Calcularemos a massa dessa fruta por meio da fórmula da alavanca:
\(F_1\cdot d_1=F_2\cdot d_2\)
Na fruta e na massa, está atuando apenas a força peso, então:
\(P_1\cdot d_1=P_2\cdot d_2\)
\(m_1\cdot g\cdot d_1=m_2\cdot g\cdot d_2\)
\(m_1\cdot10\cdot10=100\cdot10\cdot50\)
\(m_1\cdot100=50.000\)
\(m_1=\frac{50.000}{100}\)
\(m_1=500\ g\)
(Udesc) Ao se fechar uma porta, aplica-se uma força na maçaneta para ela rotacionar em torno de um eixo fixo onde estão as dobradiças. Com relação ao movimento dessa porta, analise as proposições.
I. Quanto maior a distância perpendicular entre a maçaneta e as dobradiças, menos efetivo é o torque da força.
II. A unidade do torque da força no Sl é o N.m, podendo também ser medida em Joule (J).
III. O torque da força depende da distância perpendicular entre a maçaneta e as dobradiças.
IV. Qualquer que seja a direção da força, o seu torque será não nulo, consequentemente, a porta rotacionará sempre.
Assinale a alternativa correta.
A) Somente a afirmativa II é verdadeira.
B) Somente as afirmativas I e II são verdadeiras.
C) Somente a afirmativa IV é verdadeira.
D) Somente a afirmativa III é verdadeira.
E) Somente as afirmativas II e III são verdadeiras.
Alternativa D
I. Quanto maior a distância perpendicular entre a maçaneta e as dobradiças, menos efetivo é o torque da força. (incorreta)
Quanto maior a distância perpendicular entre a maçaneta e as dobradiças, mais efetivo é o torque da força.
II. A unidade do torque da força no Sl é o N.m, podendo também ser medida em Joule (J). (incorreta)
A unidade do torque da força no Sl é o N.m, não podendo ser medida em Joule (J).
III. O torque da força depende da distância perpendicular entre a maçaneta e as dobradiças. (correta)
IV. Qualquer que seja a direção da força, o seu torque será não nulo, consequentemente, a porta rotacionará sempre. (incorreta)
Para calcular o torque, é necessário levar em consideração apenas as forças penpendiculares ao sistema de rotação.
(Fuvest) Uma criança senta-se num banco giratório com os braços encostados ao corpo e pede que façam girar o banco em torno de um eixo vertical que passa pelo centro do sistema criança-banco. Num dado instante, com o sistema criança-banco a girar solidariamente, a criança abre os braços e volta a encostá-los ao corpo.
Considere desprezível o efeito do atrito entre o banco e o eixo vertical. Selecione a afirmação verdadeira.
A) Quando a criança abre os braços, o momento de inércia do sistema, em relação ao eixo de rotação, diminui.
B) Quando a criança abre os braços, o módulo da velocidade angular do sistema diminui.
C) Quando a criança fecha os braços, o momento de inércia do banco, em relação ao seu centro de massa, diminui.
D) Quer a criança abra ou feche os braços, o módulo da velocidade angular do sistema mantém-se.
E) Quer a criança abra ou feche os braços, o momento angular do banco, em relação ao eixo de rotação, mantém-se.
Alternativa B
Quando a criança abre os braços, o momento de inércia do sistema, em relação ao eixo de rotação, diminui por causa da conservação do momento angular.
(Uerj) A figura abaixo ilustra uma ferramenta utilizada para apertar ou desapertar determinadas peças metálicas.
Para apertar uma peça, aplicando-se a menor intensidade de força possível, essa ferramenta deve ser segurada de acordo com o esquema indicado em:
A)
B)
C)
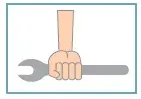
D)
Alternativa D
Nesse caso é necessário empregar a força na vertical e sobre a extremidade, já que, quanto mais longe a mão estiver do orifício de abertura, menor será a força necessária.
Qual a posição do centro de massa de um sistema de partículas de 0,005 kg posicionadas nos pontos P1 = (-3, 4); P2 = (0, 2); P3 = (5, -3).
A) (1;1)
B) (0,67;1)
C) (-2,-2)
D) (1;0,67)
E) (2;2)
Alternativa B
Primeiramente, calcularemos o centro de massa no eixo x:
\(x_{CM}=\frac{m_1\cdot x_1+m_2\cdot x_2{+m}_3\cdot x_3}{m_1+m_2+m_3}\)
\(x_{CM}=\frac{0,005\cdot\left(-3\right)+0,005\cdot0+0,005\cdot5}{0,005+0,005+0,005}\)
\(x_{CM}=\frac{-0,015\ +0+0,025\ }{0,015\ }\)
\(x_{CM}=\frac{0,010\ }{0,015\ }\)
\(x_{CM}\approx0,67\)
Por fim, calcularemos o centro de massa no eixo y:
\(y_{CM}=\frac{m_1\cdot y_1+m_2\cdot y_2{+m}_3\cdot y_3}{m_1+m_2+m_3}\)
\(y_{CM}=\frac{0,005\cdot4+0,005\cdot2+0,005\cdot(-3)}{0,005+0,005+0,005}\)
\(y_{CM}=\frac{0,02\ +0,01-0,015\ }{0,015\ }\)
\(y_{CM}=\frac{0,015\ }{0,015\ }\)
\(y_{CM}=1\)
Determine o momento angular de um objeto que possui um momento linear de 100 kg∙ms, sabendo que a sua distância até o eixo de rotação é de 2 m e que, nesse caso, o senoθ é 1.
A) 100 kg∙m2/s
B) 200 kg∙m2/s
C) 300 kg∙m2/s
D) 400 kg∙m2/s
E) 500 kg∙m2/s
Alternativa B
\(L=r\cdot p\cdot\sin{\theta}\)
\(L=2\cdot100\cdot1\)
\(L=200\ {kg\cdot m^2}/{s}\)
Duas crianças estão brincando em uma gangorra com comprimento de 12 m, com o eixo de rotação posicionado exatamente no meio dela. Considerando que a criança de 40 kg tenha se sentado na extremidade direita e a criança de 30 kg tenha se sentado na extremidade esquerda, qual será a distância da segunda criança ao eixo de rotação, a fim de que a gangorra fique em equilíbrio?
Dados: Aceleração da gravidade = 10 m/s2.
A) 4
B) 5
C) 6
D) 7
E) 8
Alternativa E
Para que a gangorra fique em equilíbrio, é necessário que os torques gerados pela força peso de cada criança sejam equivalentes, então:
\(\tau_1=\tau_2\)
\(r_1\cdot F_1=r_2\cdot F_2\)
\(r_1\cdot P_1=r_2\cdot P_2\)
\(r_1\cdot m_1\cdot g=r_2\cdot m_2\cdot g\)
\(r_1\cdot30\cdot10=6\cdot40\cdot10\)
\(r_1\cdot300=2400\)
\(r_1=\frac{2400}{300}\)
\(r_1=8\ m\)
O momento angular de um corpo é 20 kg∙m2/s e o seu momento linear é de 10 kg∙m/s. Qual é a sua distância até o eixo de rotação, considerando que o senoθ é 0,5?
A) 2 m
B) 3 m
C) 4 m
D) 5 m
E) 6 m
Alternativa C
Calcularemos a distância do corpo até o eixo de rotação:
\(L=r\cdot p\cdot s i n{\theta}\)
\(20=r\cdot10\cdot0,5\)
\(20=r\cdot5\)
\(r=\frac{20}{5}\)
\(r=4\ m\)
Determine o centro de massa entre dois corpos com massas m1 = 0,20 kg e m2 = 0,30 kg, localizadas nas coordenadas (-3, 0) e (3, 4).
A) (0,6; -2,4)
B) (-1,2; 2,4)
C) (0,6; 2,4)
D) (1,2; -2,4)
E) (-0,6; 2,4)
Alternativa C
Primeiramente, calcularemos o centro de massa no eixo x:
\(x_{CM}=\frac{m_1\cdot x_1+m_2\cdot x_2}{m_1+m_2}\)
\(x_{CM}=\frac{0,2\cdot(-3)+0,3\cdot(3)}{0,2+0,3}\)
\(x_{CM}=\frac{-0,6+0,9}{0,5}\)
\(x_{CM}=0,6\)
Por fim, calcularemos o centro de massa no eixo y:
\(y_{CM}=\frac{m_1\cdot y_1+m_2\cdot y_2}{m_1+m_2}\)
\(y_{CM}=\frac{0,2\cdot(0)+0,3\cdot(4)}{0,2+0,3}\)
\(y_{CM}=\frac{0+1,2}{0,5}\)
\(y_{CM}=2,4\)
As alavancas são amplamente usadas em nosso cotidiano, com o intuito de facilitar alguma atividade. Pensando nisso, qual dos exemplos abaixo é uma alavanca interfixa, alavanca inter-resistente e alavanca interpotente respectivamente?
A) Tesoura, quebra-nozes e cortador de unha.
B) Abridor de garrafa, pinça e tesoura.
C) Cortador de unha, carrinho de mão, gangorra.
D) Alicate, pinça, quebra-nozes.
E) Martelo, carrinho de mão, gangorra.
Alternativa A
A tesoura, o quebra-nozes e o cortador de unha são exemplos de alavancas interfixa, inter-resistente e interpotente respectivamente.
Calcule o centro de massa de um retângulo, sabendo que a sua altura é de 2 metros e a sua base é de 3 metros.
A) (1,5; 1)
B) (3; 2)
C) (4,5; 3)
D) (6; 4)
E) (7,5; 5)
Alternativa A
Para encontrar o centro de massa do retângulo, é necessário encontrar a sua posição no eixo x, dada pela metade do valor de sua base:
\(x_{CM}=\frac{b}{2}\)
\(x_{CM}=\frac{3}{2}\)
\(x_{CM}=1,5\)
Já a sua posição no eixo y é dada pela metade do valor de sua altura:
\(y_{CM}=\frac{h}{2}\)
\(y_{CM}=\frac{2}{2}\)
\(y_{CM}=1\)
Analise as alternativas abaixo referentes às unidades de medida estudadas em estática.
I. A força é medida em Newton por metro.
II. A distância é medida em metro por segundo.
III. O torque é medido em Newton por metro.
IV. O momento angular é medido em kg∙m2/s .
V. O momento linear é medido em kg∙m/s .
Está(ão) correta(s):
A) I, II e III.
B) I, IV, V.
C) II, III, IV.
D) I, II,V.
E) III, IV, V
Alternativa E
I. A força é medida em Newton por metro. (incorreta)
A força é medida em Newton.
II. A distância é medida em metro por segundo. (incorreta)
A distância é medida em metro.
III. O torque é medido em Newton por metro. (correta)
IV. O momento angular é medido em kg∙m2/s. (correta)
V. O momento linear é medido em kg∙m/s. (correta)
