Exercícios sobre fontes de campo magnético
Marque a alternativa que melhor representa o vetor indução magnética B no ponto P, gerado pela corrente elétrica que percorre o condutor retilíneo da figura abaixo.
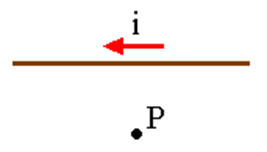
a) 
b) 
c) 
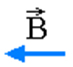
d) 
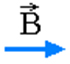
e) 
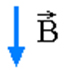
De acordo com a regra da mão direita, posicionamos o polegar no sentido da corrente elétrica e os demais dedos representam o vetor indução magnética. No ponto P, pela regra, temos o vetor saindo.
Alternativa B
Vamos supor que uma corrente elétrica de intensidade igual a 5 A esteja percorrendo um fio condutor retilíneo. Calcule a intensidade do vetor indução magnética em um ponto localizado a 2 cm do fio. Adote μ= 4π.10-7 T.m/A.
a) B = 2 . 10-5 T
b) B = 5 . 10-7 T
c) B = 3 . 10-7 T
d) B = 5 . 10-5 T
e) B = 2,5 . 10-5 T
Sabemos que a intensidade do vetor indução magnética no ponto P, devido à corrente elétrica i, é dada pela seguinte relação:
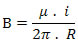
Retirando os dados fornecidos pelo exercício e substituindo-os na equação acima, temos:
i = 5 A, R = 2 cm = 0,02 = 2 . 10-2 m
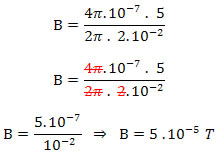
Alternativa D
Para a figura abaixo, determine o valor do vetor indução magnética B situado no ponto P e marque a alternativa correta. Adote μ = 4π.10-7 T.m/A, para a permeabilidade magnética.
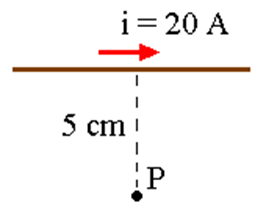
a) B = 4 . 10-5 T
b) B = 8 . 10-5 T
c) B = 4 . 10-7 T
d) B = 5 . 10-5 T
e) B = 8 . 10-7 T
Podemos determinar o valor do vetor indução magnética através da seguinte relação:
.jpg)
Da figura podemos retirar o raio e a intensidade da corrente elétrica. Assim, temos:
R= 5 cm = 0,05 m = 5 . 10-2 m e i = 20 A
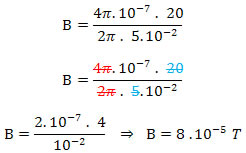
Alternativa B
Na figura abaixo temos a representação de uma espira circular de raio R e percorrida por uma corrente elétrica de intensidade i. Calcule o valor do campo de indução magnética supondo que o diâmetro dessa espira seja igual a 6πcm e a corrente elétrica seja igual a 9 A. Adote μ = 4π.10-7 T.m/A.
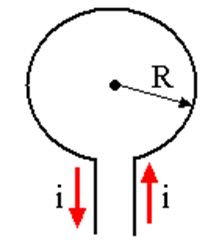
a) B = 6 . 10-5 T
b) B = 7 . 10-5 T
c) B = 8 . 10-7 T
d) B = 4 . 10-5 T
e) B = 5 . 10-7 T
Podemos determinar o vetor campo indução magnética no interior de uma espira circular através da seguinte equação:
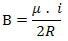
Retirando as informações fornecidas pelo exercício.
i = 9 A, μ = 4π.10-7 T.m/A e R = 3π . 10-2 m (o diâmetro é duas vezes o raio, portanto, basta dividirmos o valor do diâmetro por 2). Para passar o valor do raio para metro dividimos por 100.
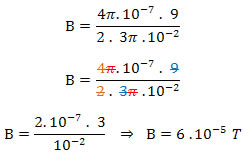
Alternativa A
