Exercícios sobre força magnética
(UFMG) Um ímã e um bloco de ferro são mantidos fixos numa superfície horizontal, como mostrado nesta figura:
Em determinado instante, ambos são soltos e movimentam-se um em direção ao outro, devido à força de atração magnética.
Despreze qualquer tipo de atrito e considere que a massa m do ímã é igual à metade da massa do bloco de ferro.
Sejam ai o módulo da aceleração e Fi o módulo da resultante das forças sobre o ímã. Para o bloco de ferro, essas grandezas são, respectivamente, af e Ff .
Com base nessas informações, é CORRETO afirmar que
a) Fi = Ff e ai = af.
b) Fi = Ff e ai = 2af.
c) Fi = 2Ff e ai = 2af.
d) Fi = 2Ff e ai = af.
LETRA “B”
A força de interação entre a placa e o ímã, por serem um sistema isolado, deve ser a mesma, portanto Fi = Ff.
Substituindo a equação da segunda lei de Newton na igualdade anterior, temos que:
Fi = Ff
m . ai = 2m . af → ai = 2 . af
(UNIP SP) A figura representa os polos de um ímã e um feixe de elétrons penetrando no campo magnético deste ímã com velocidade V, perpendicularmente ao plano do papel.
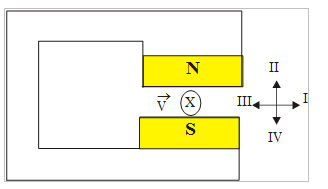
O feixe de elétrons deslocar-se-á segundo a orientação dada pela seta:
a) I
b) II
c) III
d) IV
e) nenhuma destas
LETRA “A”
O campo magnético atua sempre do polo norte para o polo sul do ímã, portanto, neste caso ele é vertical e para baixo. A força magnética, o campo magnético e a velocidade do feixe de elétrons devem ser perpendiculares entre si, assim sendo, aplicando a regra da mão direita, percebe-se que o único sentido possível para a atuação da força é sobre a seta I.
A figura mostra a tela de um osciloscópio onde um feixe de elétrons, que provém perpendicularmente da página para seus olhos, incide no centro da tela. Aproximando-se lateralmente da tela dois ímãs iguais com seus respectivos polos mostrados, verificar-se-á que o feixe:
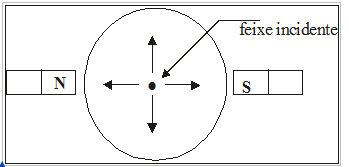
a) será desviado para cima ↑
b) será desviado para baixo ↓
c) será desviado para a esquerda ←
d) será desviado para a direita →
e) não será desviado.
LETRA “B”
O campo magnético atua sempre do polo norte para o polo sul do ímã, portanto, nesse caso ele é horizontal para a direita. A força magnética, o campo magnético e a velocidade do feixe de elétrons devem ser perpendiculares entre si, aplicando a regra da mão direita, percebe-se que a força magnética deve ser vertical e para baixo ↓.
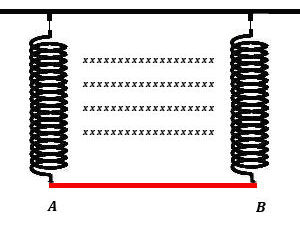
A figura abaixo ilustra duas molas flexíveis, feitas de material condutor, que sustentam uma haste AB também condutora, de 10 g de massa e 80 cm de comprimento. Sabendo que a haste está imersa em uma região de campo magnético de módulo 2 T, qual deve ser o sentido e o valor da corrente elétrica na haste para que as trações nas molas sejam nulas?
ADOTE : g = 10 m/s2 , o sinal “x” indica que o campo magnético entra no plano da página.
a) 6,25 x 10 – 2 A, atuando para a direita
b) 6,00 x 10 – 2 A, atuando para a esquerda
c) 1,25 x 10 – 2 A, atuando para a direita
d) 9,25 x 10 – 2 A, atuando para a esquerda
e) 8,25 x 10 – 2 A, atuando para a direita
LETRA “A”
Para que as trações sejam nulas sobre a haste, sua força peso deve ser oposta à força magnética. Portanto, como o peso é vertical e para baixo, a força magnética deve atuar na vertical para cima. Pela regra da mão direita para o fio retilíneo, o sentido da corrente, o campo magnético e a força magnética devem ser perpendiculares entre si, portanto, a corrente elétrica deve atuar na haste para a direita.
Igualando a força peso com a força magnética sobre fios, temos:
P = FM
m . g = B . i . L . sen90°
0,01 . 10 = 2 . i . 0,8 . 1
0,1 = 1,6 . i
i = 0,0625
i = 6,25 x 10 – 2 A
Duas placas eletrizadas estão separadas por uma distância de 2 cm e mantém entre si uma diferença de potencial de 300 V. Sabendo que por entre as placas passa uma partícula negativa com velocidade v = 2,0 x 108 m/s sem sofrer desvios por conta de um campo magnético, determine o valor deste campo entre as placas em tesla (T) que permite o trajeto retilíneo da partícula.
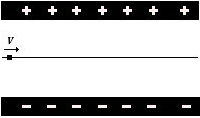
a) 7,0 x 10 – 5 T
b) 7,5 x 10 – 5 T
c) 6,5 x 10 – 5 T
d) 3,5 x 10 – 5 T
e) 5,5 x 10 – 5 T
LETRA “B”
A trajetória da partícula é retilínea por conta da atuação das forças elétrica e magnética. Essas forças devem ser iguais para que a partícula não sofra desvios, portanto:
FELÉTRICA = FMAGNÉTICA
E . q = q . v . B . sen90°
U = v . B
d
B = U
d . v
B = 300 . 2,0 x 108
0,02
B = 7,5 x 10-5 T
