Exercícios sobre a força de tração
Teste seus conhecimentos por meio desta lista de exercícios sobre força de tração, força de contato entre um corpo e um meio que o traciona.
Publicado por: Pâmella Raphaella MeloQuestões
-
Questão 1
(Uerj) Em um experimento, os blocos I e II, de massas iguais a 10 kg e a 6 kg, respectivamente, estão interligados por um fio ideal. Em um primeiro momento, uma força de intensidade F igual a 64 N é aplicada no bloco I, gerando no fio uma tração TA. Em seguida, uma força de mesma intensidade F é aplicada no bloco II, produzindo a tração TB.
Observe os esquemas:
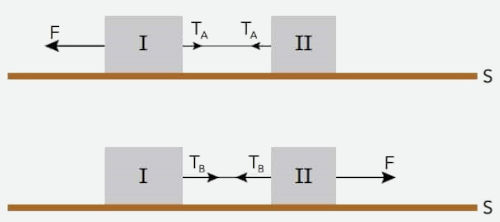
Desconsiderando os atritos entre os blocos e a superfície S, a razão entre as trações TA/TB corresponde a:
A) 9/10
B) 4/7
C) 3/5
D) 8/13
Alternativa C.
Primeiramente, calcularemos a aceleração do sistema através da fórmula da 2ª lei de Newton:
\(F_R=m\cdot a \)
\(64=(10+6)\cdot a\)
\(64 = 16 \cdot a\)
\(a= \frac{64}{16}\)
\(a=4 m/s^2 \)
Depois, calcularemos a força de tração no bloco I, através da fórmula da 2ª lei de Newton:
\(F_R=m\cdot a \)
\(T_A= m\cdot a \)
\(T_A= 6 \cdot 4 \)
\(T_A=24 N \)
E calcularemos a força de tração no bloco II, através da fórmula da 2ª lei de Newton:
\(F_R=m\cdot a \)
\(T_B= 10 \cdot 4 \)
\(T_B=40 N \)
Por fim, a razão entre as trações TA/TB será:
\(\frac{T_A}{T_B} = \frac{24}{40} = \frac{3}{5}\)
-
Questão 2
(UnB) A figura 1 representa um corpo suspenso por um fio. A figura 2 representa as forças atuantes sobre cada parte do sistema da figura 1.
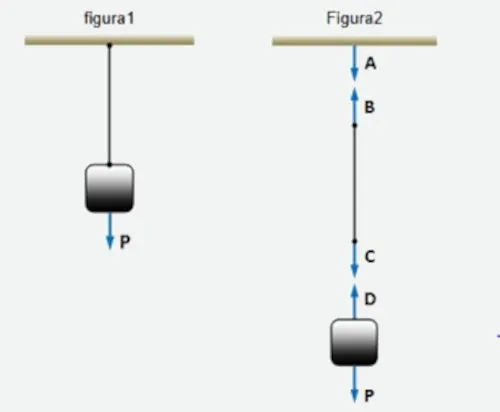
Pela lei da ação e reação, podemos afirmar que:
A) D e P formam um par ação e reação.
B) P e B formam um par ação e reação.
C) A e C formam um par ação e reação.
D) B e C formam um par ação e reação.
E) A e B formam um par ação e reação
Alternativa E.
A força de tração e a força peso não são um par ação e reação, já que atuam em um mesmo corpo, portanto somente A e B formam um par ação e reação.
-
Questão 3
(FEI) Sabendo-se que a tração no fio que une os dois blocos vale 100 N, qual é o valor do módulo da força F? Não há atritos.
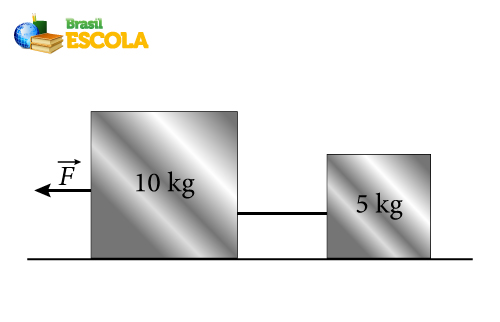
Créditos: Gabriel Franco | Brasil Escola. A) 350 N
B) 300 N
C) 400 N
D) 250 N
E) 290 NAlternativa B.
No bloco menor temos a atuação apenas da força de tração, então a expressão da força resultante, dada pela fórmula da 2ª lei de Newton, é:
\(F_R=m \cdot a\)
\(T=m_1\cdot a \)
Substituindo pelo valor da força de tração e massa do bloco, obtemos a aceleração do bloco:
\(100=5\cdot a \)
\(a = \frac{100}{5}\)
\(a = 20\ m/s^2\)
Já no bloco maior temos a atuação da força de tração e força F, então a expressão da força resultante, dada pela fórmula da 2ª lei de Newton, é:
\(F_R=m \cdot a\)
\(F-T=m_2\cdot a \)
Substituindo pelo valor da força de tração, massa do bloco e aceleração do bloco, obtemos a força F:
\(F-100=10\cdot 20 \)
\(F-100=200 \)
\(F=200 +100\)
\(F=300 N \)
-
Questão 4
(Uespi) Três corpos estão interligados por fios ideais, conforme mostrados na figura. A força de tração T sobre o bloco 1 tem intensidade igual a 150N. As massas dos blocos valem, respectivamente, m1 = 50 kg, m2 = 30 kg e m3 = 20 kg. As trações T1, no fio entre os blocos 1 e 2, e T2, entre os blocos 2 e 3, têm intensidades respectivamente iguais a:
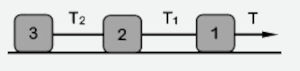
A) 75 N e 45 N
B) 75 N e 30 N
C) 45 N e 75 N
D) 40 N e 30 N
E) 30 N e 75 N
Alternativa B.
No bloco 3 temos a atuação apenas da força de tração T2 , então a expressão da força resultante, dada pela fórmula da 2ª lei de Newton, é:
\(F_R = m \cdot a\)
\(T_2=m_3\cdot a \)
\(T_2=20\cdot a \)
Já no bloco 2 temos a atuação da força de tração T2 e T1, então a expressão da força resultante, dada pela fórmula da 2ª lei de Newton é:
\(F_R = m \cdot a\)
\(T_1 - T_2=m_2\cdot a \)
\(T_1 - T_2=30 \cdot a \)
E no bloco 1 temos a atuação da força de tração T e T1, então a expressão da força resultante, dada pela fórmula da 2ª lei de Newton, é:
\(F_R = m \cdot a\)
\(T - T_1=m_1\cdot a \)
\(150 - T_1=50\cdot a \)
As expressões obtidas compõem o sistema:
\( \begin{cases} T_2 &= 20 \cdot a \\ T_1 - T_2 &= 30 \cdot a \\ 150 - T_1 &= 50 \cdot a \end{cases}\)
Somando as equações, obtemos:
\(150=20\cdot a+30\cdot a+50\cdot a \)
\(150=100\cdot a \)
\(a= \frac{150}{100}\)
\(a=1,5 m/s^2 \)
Substituindo na expressão do bloco 1, encontramos a tração T1:
\(150-T_1=50\cdot a \)
\(150-T_1=50\cdot 1,5\)
\(150-T_1=75\)
\(T_1=75 N \)
Substituindo na expressão do bloco 3, encontramos a tração T2 :
\(T_2=20\cdot a \)
\(T_2=20\cdot 1,5\)
\(T_2=30 N\)
-
Questão 5
Um bloco de 1,5 kg está suspenso por uma corda presa ao teto. Sabendo que a aceleração da gravidade é igual a 10 m/s2, calcule a intensidade da força de tração na corda.
A) 1,5 N
B) 2,0 N
C) 2,5 N
D) 3,0 N
E) 3,5 N
Alternativa A.
Nessa situação, a força de tração será igual à força peso, então calcularemos a intensidade da força de tração na corda através da fórmula da força peso:
\(T = P\)
\(T=m\cdot g \)
\(T=1,5 \cdot 10 \)
\(T=15 N \)
-
Questão 6
Determine a massa de um bloco que é puxado por uma corda com uma força de 900 N ao longo de uma superfície horizontal e se movimenta com aceleração de 2 m/s2. Desconsidere o atrito.
A) 350 kg
B) 400 kg
C) 450 kg
D) 500 kg
E) 550 kg
Alternativa C.
Calcularemos a massa do bloco através da fórmula da 2ª lei de Newton, em que a força resultante é a força de tração:
\(F_R=m\cdot a \)
\(T=m\cdot a \)
\(900=m\cdot 2 \)
\(m = \frac{900}{2}\)
\(m=450 kg \)
-
Questão 7
Um bloco de 20 kg está suspenso por uma corda presa ao teto. Sabendo que a aceleração da gravidade é igual a 10 m/s2, qual deve ser a intensidade da força de tração na corda?
A) 50 N
B) 100 N
C) 200 N
D) 300 N
E) 400 N
Alternativa D.
Nessa situação, a força de tração será igual à força peso, então calcularemos a intensidade da força de tração na corda através da fórmula da força peso:
\(T=P \)
\(T=m\cdot g \)
\(T=20\cdot 10 \)
\(T=200 N \)
-
Questão 8
A respeito da força de tração, qual das forças abaixo é o seu par ação e reação?
A) força normal
B) força elétrica
C) força peso
D) força de atrito
E) nenhuma das opções
Alternativa E.
O par ação e reação da força de tração não é a força normal, a força elétrica, a força peso nem a força de atrito, mas sim a força de reação do corpo à força de tração.
-
Questão 9
Determine a intensidade da força de tração em uma corda presa a uma caixa de 100 kg; considere a aceleração da gravidade igual a 10 m/s2.
A) 250 N
B) 500 N
C) 750 N
D) 1000 N
E) 2000 N
Alternativa D.
Nessa situação, a força de tração será igual à força peso, então calcularemos a intensidade da força de tração na corda através da fórmula da força peso:
\(T=P \)
\(T=m\cdot g \)
\(T=100\cdot 10\)
\(T=1000 N \)
-
Questão 10
Qual deve ser a aceleração de um bloco de 8 kg que é puxado por uma corda com uma força de 100 N ao longo de uma superfície horizontal? Desconsidere o atrito.
A) 10,0 m/s2
B) 12,5 m/s2
C) 14,0 m/s2
D) 16,5 m/s2
E) 18,0 m/s2
Alternativa B.
Calcularemos a aceleração do bloco através da fórmula da 2ª lei de Newton, em que a força resultante é a força de tração:
\(F_R=m\cdot a \)
\(T=m\cdot a \)
\(100=8\cdot a \)
\(a=\frac{100}{8}\)
\(a=12,5 m/s^2 \)
-
Questão 11
A força de tração pode ser classificada como uma força de:
A) força de contato
B) força interna
C) força de atrito
D) força intensa
E) força de atração
Alternativa A.
A força de tração é classificada como uma força de contato entre um corpo e um meio que o traciona, como uma corda, fio, cabo.
-
Questão 12
Quais das alternativas apresentam as unidades de medidas relacionadas à força de tração?
I. A massa é medida em quilograma cúbico.
II. A força peso é medida em Newton.
III. A força de tração é medida em Newton por metro.
IV. A aceleração da gravidade é medida em metros por segundo ao quadrado.
A) Alternativas I e II.
B) Alternativas II e III.
C) Alternativas III e IV.
D) Alternativas I e IV.
E) Alternativas II e IV.
Alternativa E.
I. A massa é medida em quilograma cúbico. (incorreta)
A massa é medida em quilograma.
II. A força peso é medida em Newton. (correta)
III. A força de tração é medida em Newton por metro. (incorreta)
A força de tração é medida em Newton.
IV. A aceleração da gravidade é medida em metros por segundo ao quadrado. (correta)