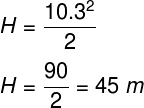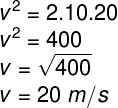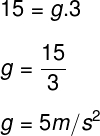Exercícios sobre funções horárias de queda livre
Um corpo é abandonado do alto de um prédio e chega ao solo exatamente 3 s após ter sido solto. Sendo a gravidade local igual a 10 m/s², a altura do prédio, em metros, é de:
a) 90 m
b) 45 m
c) 30 m
d) 150 m
e) 100 m
Letra B
Quando um corpo em repouso inicia o seu movimento, passando a descrever um movimento de queda livre, é possível calcular a sua altura pela equação a seguir:
Substituindo as variáveis da equação acima pelos dados fornecidos pelo exercício, teremos a seguinte igualdade:
De acordo com o nosso cálculo, a altura do prédio deve ser de 45 m.
Um objeto cai, a partir do repouso, de cima de uma superfície, chegando ao solo em 4 s. A velocidade desse objeto, imediatamente antes de tocar o solo, em km/h, é igual a:
a) 18 km/h
b) 180 km/h
c) 72 km/h
d) 90 km/h
e) 144 km/h
Letra E
A aceleração da gravidade tem valor constante. Dessa forma, o movimento de queda livre pode ser entendido como um Movimento Retilíneo Uniformemente Variado (MRUV). Com isso, podemos calcular a velocidade do objeto durante a queda com a equação a seguir:
Tomando os dados fornecidos pelo enunciado do exercício, teremos a seguinte igualdade:
Na resolução acima, multiplicamos 40 m/s pelo fator 3,6 para converter a unidade de m/s para km/h, resultando em uma velocidade de 144 km/h.
Um corpo é abandonado de uma altura de 20,0 m e cai em direção ao solo, em uma região onde a aceleração da gravidade é igual a 10 m/s². A velocidade desse corpo imediatamente antes de tocar o solo é igual a:
a) 200 m/s
b) 15,0 m/s
c) 20,0 m/s
d) 5,0 m/s
e) 25,0 m/s
Letra C
O exercício pede que encontremos o valor da velocidade de um corpo após cair de uma altura de 20,0 m imediatamente antes de tocar o solo. No entanto, o enunciado não fornece qualquer intervalo de tempo e, por isso, devemos utilizar a equação de Torricelli para a queda livre:
Tomando as informações contidas no enunciado do exercício, teremos:
Dessa forma, a velocidade final do corpo em queda livre é de 20 m/s.
Um objeto é solto de uma posição alta e leva 3,0 s para atingir a velocidade de 15,0 m/s. A aceleração de gravidade nesse local é de:
a) 3,0 m/s²
b) 10,0 m/s²
c) 9,8 m/s²
d) 4,0 m/s²
e) 5,0 m/s²
Letra E
A equação capaz de relacionar a velocidade e o tempo da queda livre com a aceleração da gravidade é:
.jpg){kind=small}
Tomando os dados fornecidos pelo enunciado do exercício, teremos:
A aceleração da gravidade nesse local é de 5,0 m/s².
