Exercícios sobre a gravitação universal
(Fuvest) No sistema solar, o planeta Saturno tem massa cerca de 100 vezes maior do que a da Terra e descreve uma órbita, em torno do Sol, a uma distância média 10 vezes maior do que a distância média da Terra ao Sol (valores aproximados). A razão FSat/FT entre a força gravitacional com que o Sol atrai Saturno e a força gravitacional com que o Sol atrai a Terra é de aproximadamente:
a) 1000
b) 10
c) 1
d) 0,1
e) 0,001
LETRA C
Primeiramente, encontraremos a expressão da força gravitacional entre Saturno e o Sol, por meio da fórmula da lei da gravitação universal:
\(F_{Sat}=G\cdot\frac{M_{Sat}\cdot m_{Sol}}{{d_{Sat}}^2}\)
Como a massa de Saturno é 100 vezes a massa da Terra, e Saturno está a uma distância média 10 vezes maior do que a distância média da Terra ao Sol, temos:
\(F_{Sat}=G\cdot\frac{100\cdot M_T\cdot m_{Sol}}{\left({10\cdot d}_T\right)^2}\)
\(F_{Sat}=G\cdot\frac{100\cdot M_T\cdot m_{Sol}}{100\cdot{d_T}^2}\)
Depois, encontraremos a expressão da força gravitacional entre a Terra e o Sol, utilizando a fórmula da lei da gravitação universal:
\(F_T=G\cdot\frac{M_T\cdot m_{Sol}}{{d_T}^2}\)
Por fim, encontraremos a razão FSat/FT :
\(\frac{F_{Sat}}{F_T}=\frac{G\cdot\frac{100\cdot M_T\cdot m_{Sol}}{100\cdot{d_T}^2}}{G\cdot\frac{M_T\cdot m_{Sol}}{{d_T}^2}}\)
\(\frac{F_{Sat}}{F_T}=\frac{G\cdot100\cdot M_T\cdot m_{Sol}}{100\cdot{d_T}^2}\ \cdot\frac{{d_T}^2}{{G\cdot M}_T\cdot m_{Sol}}\)
Eliminando os termos semelhantes, obtemos:
\(\frac{F_{Sat}}{F_T}=\frac{100}{100}\ \)
\(\frac{F_{Sat}}{F_T}=1\ \)
(Enem) Observações astronômicas indicam que no centro de nossa galáxia, a Via Láctea, provavelmente exista um buraco negro cuja massa é igual a milhares de vezes a massa do Sol. Uma técnica simples para estimar a massa desse buraco negro consiste em observar algum objeto que orbite ao seu redor e medir o período de uma rotação completa, T, bem como o raio médio, R, da órbita do objeto, que supostamente se desloca, com boa aproximação, em movimento circular uniforme. Nessa situação, considere que a força resultante, devido ao movimento circular, é igual, em magnitude, à força gravitacional que o buraco negro exerce sobre o objeto.
Considerando o período de rotação, a distância média e a constante gravitacional, G, a massa do buraco negro é
a) \(\frac{4∙π²∙R^2}{G∙T²}\)
b) \(\frac{π²∙R^3}{2∙G∙T²}\)
c) \(\frac{2∙π²∙R^3}{G∙T²}\)
d) \(\frac{4∙π²∙R^3}{G∙T²}\)
e) \(\frac{π²∙R^5}{G∙T²}\)
LETRA D
Primeiramente, calcularemos a velocidade do buraco negro:
\(v=\frac{∆x}{∆t} +\)
A distância percorrida equivale ao comprimento de uma circunferência, e a variação de tempo equivale ao período de uma rotação completa, então:
\(v=\frac{2\cdot\pi\cdot R}{T}\)
Depois, calcularemos a força centrípeta:
\(F_C=m\cdot\frac{v^2}{R}\)
\(F_C=m\cdot\frac{\left(\frac{2\cdot\pi\cdot R}{T}\right)^2}{R}\)
\(F_C=m\cdot\frac{\frac{4\cdot\pi^2\cdot R^2}{T^2}}{R}\)
\(F_C=m\cdot\frac{4\cdot\pi^2\cdot R^2}{T^2}\cdot\frac{1}{R}\)
\(F_C=m\cdot\frac{4\cdot\pi^2\cdot R}{T^2}\)
Como a força centrípeta é igual à força de interação gravitacional, temos:
\(F_G=F_C\)
\(G\cdot\frac{M\cdot m}{R^2}=\ \frac{4\cdot\pi^2\cdot R\cdot m}{T^2}\)
\(M=\ \frac{4\cdot\pi^2\cdot R\cdot m\cdot R^2}{T^2\cdot m\cdot G}\)
\(M=\ \frac{4\cdot\pi^2\cdot R^3}{G\cdot T^2}\)
(Udesc-SC) A maré é o fenômeno natural de subida e descida do nível das águas, percebido principalmente nos oceanos, causado pela atração gravitacional do Sol e da Lua. A ilustração a seguir esquematiza a variação do nível das águas ao longo de uma rotação completa da Terra. Considere as seguintes proposições sobre maré e assinale a alternativa incorreta.
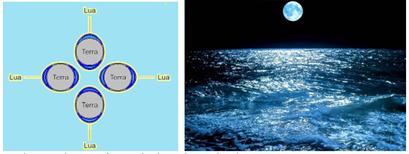
a) As marés de maior amplitude ocorrem próximo das situações de Lua nova ou Lua cheia, quando as forças atrativas, devido ao Sol e à Lua, se reforçam mutuamente.
b) A influência da Lua é maior do que a do Sol, pois embora a sua massa seja muito menor do que a do Sol, esse fato é compensado pela menor distância à Terra.
c) A maré cheia é vista por um observador quando a Lua passa por cima dele ou quando a Lua passa por baixo dele.
d) As massas de água que estão mais próximas da Lua ou do Sol sofrem atração maior do que as massas de água que estão mais afastadas, devido à rotação da Terra.
e) As marés alta e baixa sucedem-se em intervalos de aproximadamente 6 horas.
LETRA D
Todas as alternativas estão corretas, com excessão da alternativa D, porque a atração gravitacional entre as massas não varia com a rotação.
(Unicamp-SP) Em setembro de 2010, Júpiter atingiu a menor distância da Terra em muitos anos. As figuras abaixo ilustram a situação de maior afastamento e a de maior aproximação dos planetas, considerando que suas órbitas são circulares, que o raio da órbita terrestre (RT) mede \(1,5\cdot{10}^{11}\ m\) e que o raio da órbita de Júpiter (RJ) equivale a \(7,5\cdot{10}^{11}\ m\).
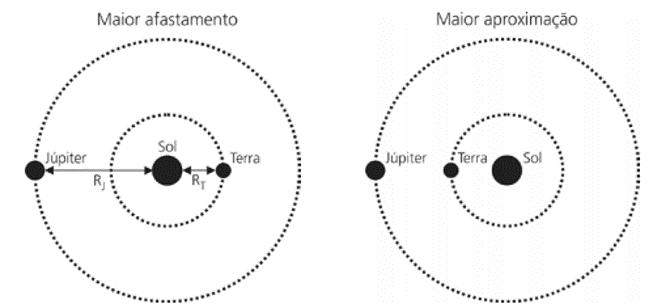
A força gravitacional entre dois corpos de massas m1 e m2 tem módulo \( F=G\cdot\frac{m_1\cdot m_2}{r^2}\) , em que r é a distância entre eles e \(G\cong6,7\ \cdot\ {10}^{-11}\ N.m^2/{kg}^2\). Sabendo que a massa de Júpiter é \(m_J=2,0\cdot{10}^{27}kg\) e que a massa da Terra é mT=6,0∙1024kg , o módulo da força gravitacional entre Júpiter e a Terra no momento de maior proximidade é
a) 1,4 ∙ 1018 N
b) 2,2 ∙ 1018 N
c) 3,5 ∙ 1019 N
d) 1,3 ∙ 1030 N
LETRA B
Calcularemos a força gravitacional entre Júpiter e a Terra por meio da fórmula da lei da gravitação universal:
\(F=G\cdot\frac{m_1\cdot m_2}{r^2}\)
\(F=\frac{6,7\ \cdot\ {10}^{-11}\cdot2,0\cdot{10}^{27}\cdot6,0\cdot{10}^{24}}{{(7,5\cdot{10}^{11}-1,5\cdot{10}^{11})}^2}\)
\(F=\frac{6,7\ \cdot\ {10}^{-11}\cdot2,0\cdot{10}^{27}\cdot6,0\cdot{10}^{24}}{{(6\cdot{10}^{11})}^2}\)
\(F=\frac{80,4\ \cdot\ {10}^{-11+27+24}}{36\cdot{10}^{22}}\)
\(F=\frac{80,4\ \cdot\ {10}^{40}}{36\cdot{10}^{22}}\)
\(F\cong2,23\ \cdot\ {10}^{40-22}\)
\(F\cong2,23\ \cdot\ {10}^{18}\ N\)
Sabendo que a força gravitacional entre dois corpos celestes é proporcional ao produto da massa dos corpos e inversamente proporcional ao quadrado da distância entre esses corpos, qual será o valor da força gravitacional quando a distância entre os dois corpos quadruplicar?
a) \(F\prime=F\)
b) \(F=\frac{F\prime}{4}\)
c) \(F\prime=\frac{F}{4}\)
d) \(F\prime=\frac{F}{16}\)
e) \(F=\frac{F'}{16}\)
LETRA D
Primeiramente, encontraremos a expressão da força gravitacional inicial por meio da fórmula da lei da gravitação universal:
\(F=G\cdot\frac{m_1\cdot m_2}{r^2}\)
Depois, encontraremos a expressão da força gravitacional depois da alteração da distância:
\(F\prime=G\cdot\frac{{m\prime}_1\cdot{m\prime}_2}{{r\prime}^2}\)
As massas se mantiveram as mesmas, e a constante de gravitação universal também. Já a distância foi quadruplicada do seu valor anterior, então:
\(F\prime=G\cdot\frac{m_1\cdot m_2}{\left(4\cdot r\right)^2}\)
\(F\prime=G\cdot\frac{m_1\cdot m_2}{16{\cdot r}^2}\)
\(F\prime=\frac{F}{16}\)
Determine a intensidade da força gravitacional entre dois corpos com 1000 kg e 800 kg, distantes em 50 metros. Considere a constante de gravitação universal como \(6,7\ \cdot\ {10}^{-11}\ N.m^2/{kg}^2\) .
a) 2,144 ∙10-6 N
b) 2,144 ∙10-7 N
c) 2,144 ∙10-8 N
d) 2,144 ∙10-9 N
e) 2,144 ∙10-10 N
LETRA C
Calcularemos a intensidade da força gravitacional entre esses corpos utilizando a fórmula da lei da gravitação universal:
\(F=G\cdot\frac{m_1\cdot m_2}{r^2}\)
\(F=6,7\ \cdot\ {10}^{-11}\cdot\frac{1000\cdot800}{{50}^2}\)
\(F=6,7\ \cdot\ {10}^{-11}\cdot\frac{1000\cdot800}{2500}\)
\(F=6,7\ \cdot\ {10}^{-11}\cdot\frac{1\cdot{10}^3\cdot8\cdot{10}^2}{2,5\cdot{10}^3}\)
\(F=\frac{53,6\cdot{10}^{-11+3+2}}{2,5\cdot{10}^3}\)
\(F=\frac{53,6\cdot{10}^{-6}}{2,5\cdot{10}^3}\)
\(F=21,44\cdot{10}^{-6-3}\)
\(F=21,44\cdot{10}^{-9}\)
\(F=2,144\cdot{10}^1\cdot{10}^{-9}\)
\(F=2,144\cdot{10}^{1-9}\)
\(F=2,144\cdot{10}^{-8}\ N\)
Sabendo que a intensidade da força gravitacional entre a Terra e a Lua é F, qual seria seu novo valor de intensidade caso triplicassem a massa da Terra e a massa da Lua, mas mantivessem a distância?
a) \(F\prime=9\cdot F\)
b) \(F\prime=F\)
c) \(F\prime=\frac{F}{9}\)
d) \(F\prime=\frac{1}{F}\)
e) \(F\prime=3\cdot F\)
LETRA A
Primeiramente, encontraremos a expressão da força gravitacional entre a Terra e a Lua antes, por meio da fórmula da lei da gravitação universal:
\(F=G\cdot\frac{m_T\cdot m_L}{r^2}\)
Depois, encontraremos a expressão da força gravitacional entre a Terra e a Lua depois, utilizando a mesma fórmula:
\(F\prime=G\cdot\frac{{m\prime}_T\cdot{m\prime}_L}{{r\prime}^2}\)
\(F\prime=G\cdot\frac{3\cdot m_T\cdot3\cdot m_L}{r^2}\)
\(F\prime=9\cdot G\cdot\frac{m_T\cdot m_L}{r^2}\)
\(F\prime=9\cdot F\)
Com base em seus estudos a respeito da lei da gravitação universal, qual dos cientistas abaixo foi o responsável pela sua formulação?
a) Isaac Newton
b) Johannes Kepler
c) Galileu Galilei
d) Giordano Bruno
e) Tycho Brahe
LETRA A
A lei da gravitação universal foi formulada pelo cientista Isaac Newton e publicada em seu livro Princípios Matemáticos da Filosofia Natural em 1687.
Qual a intensidade aproximada da força de atração gravitacional entre o Sol, cuja massa é \(2\cdot{10}^{30}\ kg\), e a Terra, cuja massa é \(6\cdot{10}^{24}\ kg\), estando a uma distância de \(1,5\cdot{10}^{11}\ m\) ? Considere a constante de gravitação universal como \(6,7\ \cdot\ {10}^{-11}\ N.m^2/{kg}^2\).
a) 7,54∙1022 N
b) 6,41∙1022 N
c) 5,98∙1022 N
d) 4,73∙1022 N
e) 3,57∙1022 N
LETRA E
Calcularemos a força gravitacional entre o Sol e a Terra utilizando a fórmula da lei da gravitação universal:
\(F=G\cdot\frac{m_1\cdot m_2}{r^2}\)
\(F=\frac{6,7\ \cdot\ {10}^{-11}\cdot2\cdot{10}^{30}\cdot6\cdot{10}^{24}}{{(1,5\cdot{10}^{11})}^2}\)
\(F=\frac{6,7\ \cdot\ {10}^{-11}\cdot2\cdot{10}^{30}\cdot6\cdot{10}^{24}}{2,25\cdot{10}^{22}}\)
\(F=\frac{80,4\ \cdot\ {10}^{-11+30+24}}{2,25\cdot{10}^{22}}\)
\(F=\frac{80,4\ \cdot\ {10}^{43}}{2,25\cdot{10}^{22}}\)
\(F\cong35,7\ \cdot\ {10}^{43-22}\)
\(F\cong35,7\ \cdot\ {10}^{21}\)
\(F\cong3,57\ \cdot{10}^1\ \cdot{10}^{21}\)
\(F\cong3,57\ \cdot{10}^{1+21}\ \)
\(F\cong3,57\ \cdot{10}^{22}\ N\ \)
Um foguete está a uma distância D do planeta X e d do planeta Y. Sabendo que a razão entre as massas do planeta X e do planeta Y é 144, determine a razão D/d de modo que as forças de atração entre os planetas e o foguete estejam em equilíbrio.
a) 3
b) 9
c) 12
d) 15
e) 18
LETRA C
Primeiramente, encontraremos a expressão da força gravitacional entre o foguete e o planeta X, por meio da fórmula da lei da gravitação universal:
\(F_X=G\cdot\frac{m_F\cdot m_X}{D^2}\)
Depois, encontraremos a expressão da força gravitacional entre o foguete e o planeta Y, utilizando a mesma fórmula:
\(F_Y=G\cdot\frac{m_F\cdot m_Y}{d^2}\)
Igualando as forças gravitacionais dos planetas com o foguete, temos:
\(F_X=F_Y\)
\(G\cdot\frac{m_F\cdot m_X}{D^2}=G\cdot\frac{m_F\cdot m_Y}{d^2}\)
Eliminando os termos semelhantes:
\(\frac{m_X}{D^2}=\frac{m_Y}{d^2}\)
\(\frac{d^2}{D^2}=\frac{m_Y}{m_X}\)
\(\frac{D^2}{d^2}=\frac{m_X}{m_Y}\)
\(\frac{D^2}{d^2}=144\)
\(\frac{D}{d}=\sqrt{144}\)
\(\frac{D}{d}=12\)
Determine a distância aproximada entre dois corpos de massas 5000 kg e 9000 kg, sabendo que entre eles ocorre uma força de atração gravitacional de 3\(3\cdot{10}^{-7}\ N\). Considere a constante de gravitação universal como \(6,7\ \cdot\ {10}^{-11}\ N.m^2/{kg}^2\) .
a) 200,4 m
b) 100,2 m
c) 50,1 m
d) 25,05 m
e) 12,5 m
LETRA B
Calcularemos a distância entre esses corpos por meio da fórmula da lei da gravitação universal:
\(F=G\cdot\frac{m_1\cdot m_2}{r^2}\)
\(3\cdot{10}^{-7}=6,7\ \cdot\ {10}^{-11}\cdot\frac{5000\cdot9000}{r^2}\)
\(r^2=6,7\ \cdot\ {10}^{-11}\cdot\frac{5\cdot{10}^3\cdot9\cdot{10}^3}{3\cdot{10}^{-7}}\)
\(r^2=\frac{301,5\cdot{10}^{-11+3+3}}{3\cdot{10}^{-7}}\)
\(r^2=\frac{301,5\cdot{10}^{-5}}{3\cdot{10}^{-7}}\)
\(r^2=100,5\cdot{10}^{-5+7}\)
\(r^2=100,5\cdot{10}^2\)
\(r=\sqrt{100,5\cdot{10}^2}\)
\(r\cong100,2\ m\)
Quais das alternativas apresentam as unidades de medida corretas das grandezas físicas estudadas em gravitação universal?
I. A força é medida em Joule.
II. A massa gravitacional ativa é medida em quilograma.
III. A massa gravitacional passiva é medida em metros.
IV. A distância é medida em metros quadrados.
V. A constante de gravitação universal é medida em Newton.
a) Alternativas I e II.
b) Alternativas III e IV.
c) Alternativas I e V.
d) Alternativas II e III.
e) Alternativas II e IV.
LETRA E
Apenas as alternativas II e IV estão corretas. Abaixo, em vermelho, vemos a correção das outras alternativas.
I. Incorreta. A força é medida em Newton.
II. Correta.
III. Incorreta. A massa gravitacional passiva é medida em quilogramas.
IV. Correta.
V. Incorreta. A constante de gravitação universal é medida em N.m2/kg2 .
