Exercícios sobre impulso de uma força variável
Na interação entre dois corpos, a força varia com o tempo. Nesse caso, o impulso da força variável em um intervalo de tempo é dado através do cálculo da área da figura.
Publicado por: Domiciano Correa Marques da SilvaQuestões
-
Questão 1
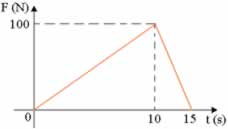
Um objeto de 2 kg, inicialmente em repouso sobre um plano horizontal, fica submetido a uma força F resultante, também horizontal, cuja intensidade varia com o tempo de acordo com o gráfico a seguir. Determine a intensidade do impulso da força F entre os instantes t0 = 0 e t = 15 s.
a) 710 N.s
b) 720 N.s
c) 730 N.s
d) 740 N.s
e) 750 N.sO gráfico de F em função do tempo t delineia um triângulo. O impulso da força F é numericamente igual à área delimitada pelo gráfico e pelo eixo das abscissas.
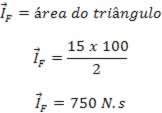
Alternativa E
-
Questão 2
Imagine uma partícula, cuja massa é 4kg, inicialmente parada sobre uma superfície. Suponha que tal partícula seja puxada verticalmente para cima por uma força de 100 N durante um intervalo de tempo igual a 4 segundos. Considere g = 10 m/s2 e despreze a resistência do ar. Determine o módulo da velocidade da partícula ao fim dos 4 s e marque a alternativa correta.
a) 20 m/s
b) 40 m/s
c) 60 m/s
d) 80 m/s
e) 10 m/sApenas duas forças atuam na partícula: o peso (
.jpg) ) e a força aplicada (
) e a força aplicada (.jpg) ).
).- intensidade da força peso:
P=m .g ⟹ P=4 .10 ⟹ P=40 m/s2
- intensidade da força resultante:
FR=F-P ⟹ FR=100-40
FR=60 NAplicando o teorema do impulso, temos:
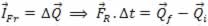
Então:
.jpg) .∆t=m .v-m .v0
.∆t=m .v-m .v0
60 .4=4v-4 .0
240=4v ⟹ v=60 m/sAlternativa C
-
Questão 3
Imagine a seguinte situação: um jogador de vôlei realiza um saque perfeito. Ao realizar o saque sobre a bola, de massa 400 g, o jogador, durante um tempo de 0,16 segundo, aplica sobre a bola uma força de 100 N. Determine o módulo da velocidade da bola imediatamente após a aplicação dessa força e marque a alternativa correta.
a) 40 m/s
b) 30 m/s
c) 60 m/s
d) 10 m/s
e) 15 m/sRetirada dos dados:
m=400g→m=0,4 kg
F=100 N
t=0,16 s
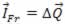
F.t=m.v-m.v0
100 .0,16=0,4 .v-0,4 .0
v=40 m/s
Alternativa A
-
Questão 4
Um objeto cai em cima de um colchão de ar, recebendo um impulso de 600 N.s e parando 0,5 s depois do impacto inicial. Qual é a força média que atua sobre ele?
a) 120 N
b) 240 N
c) 600 N
d) 1200 N
e) 500 NFazendo uso da definição de impulso e notando que o impulso e a força possuem mesma direção e sentido, podemos calcular a força. Partindo da equação do impulso, podemos escrever:
I=F.∆t
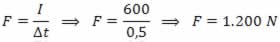
Alternativa D