Exercícios sobre impulso
(UFSM) Assinale falsa (F) ou verdadeira (V) em cada uma das afirmativas. Sobre a grandeza física impulso, pode-se afirmar:
I. O impulso é uma grandeza instantânea.
II. A direção e o sentido do impulso são os mesmos da força aplicada sobre o corpo.
III. A força que produz o impulso é causada pela interação dos corpos que colidem.
IV. O impulso mede a quantidade de movimento do corpo.
A sequência correta é:
A) V – V – F – F
B) F – V – V – F
C) V – F – V – V
D) F – F – F – V
E) F – V – V – V
Alternativa B.
I. O impulso é uma grandeza instantânea. (incorreta)
O impulso é uma grandeza vetorial.
II. A direção e o sentido do impulso são os mesmos da força aplicada sobre o corpo. (correta)
III. A força que produz o impulso é causada pela interação dos corpos que colidem. (correta)
IV. O impulso mede a quantidade de movimento do corpo. (incorreta)
O impulso mede a variação da quantidade de movimento do corpo.
(UFMT) Um corpo de peso igual a 100 N é lançado verticalmente para cima, atingindo a altura máxima em 1,0 s. O impulso aplicado a esse corpo pela força da gravidade, durante a subida, tem módulo, em N · s, igual a:
A) zero
B) 10
C) 50
D) 100
E) 500
Alternativa D.
Calcularemos o impulso aplicado a esse corpo empregando a sua fórmula:
\(I = F \cdot \Delta t \)
\(I = 100 \cdot 1 \)
\(I = 100\ N\cdot s \)
(Unipac) Um automóvel cuja massa é de 900 kg desenvolve velocidade de 108 km/h (30 m/s), quando o motorista pisa bruscamente no freio e, com desaceleração constante, consegue parar após 5,0 segundos. Pode-se afirmar que a variação da quantidade de movimento do automóvel foi:
A) 5,4∙103 N·s
B) 2,7∙104 N·s
C) 9,7∙104 N·s
D) zero
Alternativa B.
Calcularemos a variação da quantidade de movimento do automóvel empregando a fórmula do teorema do impulso à quantidade de movimento:
\(I = \Delta p\)
\(F \cdot \Delta t = \Delta p\)
\(m\cdot a \cdot \Delta t = \Delta p\)
\(m\cdot \frac{\Delta v}{\Delta t} \cdot \Delta t = \Delta p\)
\(m\cdot \Delta v = \Delta p\)
\(900\cdot (0-30)=\Delta p\)
\(900\cdot (-30)=\Delta p\)
\(-27000=\Delta p\)
\(-2,7\cdot 10^4 =\Delta p\)
Então, em módulo:
\(2,7\cdot 10^4 N\cdot s=\Delta p\)
(PUC) O gráfico representa a força resultante sobre um carrinho de supermercado de massa total 40 kg, inicialmente em repouso.
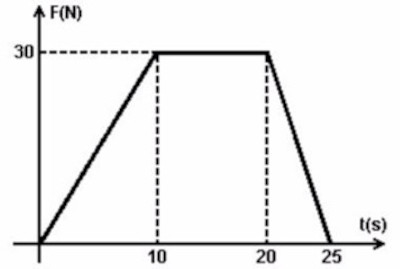
A intensidade da força constante que produz o mesmo impulso que a força representada no gráfico durante o intervalo de tempo de 0 a 25 s é, em newtons, igual a:
A) 2
B) 12
C) 15
D) 20
E) 21
Alternativa E.
Primeiramente, calcularemos o impulso empregando a fórmula da área do trapézio:
\(I = \frac{(B+b)\cdot h}{2}\)
\(I = \frac{(25+10)\cdot 30}{2}\)
\(I = 525 N\cdot s\)
Por fim, calcularemos a intensidade da força constante que produz o mesmo impulso por meio da fórmula do impulso:
\(I = F\cdot \Delta t\)
\(525 = F\cdot 25\)
\(F = \frac{525}{25}\)
\(F=21 N \)
Sabendo que a variação da quantidade de movimento de um corpo foi de 800 kg·m/s, calcule o impulso.
A) 400 N·s
B) 600 N·s
C) 800 N·s
D) 1000 N·s
E) 1200 N·s
Alternativa C.
Calcularemos o impulso por meio da fórmula que o relaciona à variação da quantidade de movimento:
\(I = \Delta p\)
\(I=800 N\cdot s \)
Qual o tempo de contato da força sobre o corpo quando é aplicada uma força de 2000 N, gerando um impulso de 500 N·s?
A) 4 s
B) 8 s
C) 12 s
D) 16 s
E) 20 s
Alternativa A.
Calcularemos o tempo de contato da força empregando a fórmula do impulso:
\(I=F\cdot \Delta t\)
\(500=2000\cdot \Delta t\)
\(\Delta t =\frac{2000}{500}\)
\(\Delta t = 4s \)
O impulso ocasionado por uma força constante ao longo do tempo resultou em um gráfico linear, então o impulso será igual à área do:
A) triângulo.
B) cilindro.
C) círculo.
D) retângulo.
E) trapézio.
Alternativa D.
Nessa situação, o impulso ocasionado por uma força constante ao longo do tempo resultou em um gráfico com uma linha, então o impulso será igual à área do retângulo, que é a área delimitada por essa linha.
Uma pedra está em repouso até que uma pessoa a chuta com uma força constante de 35 N durante 0,1 segundo. Com base nisso, calcule o impulso recebido pela pedra durante o chute. Considere que a direção da força seja a mesma da direção do chute.
A) 1,6 N·s
B) 2,7 N·s
C) 3,5 N·s
D) 4,8 N·s
E) 5,9 N·s
Alternativa C.
Calcularemos o impulso por meio da sua fórmula:
\(I= F\cdot \Delta t\)
\(I= 35\cdot 0,1\)
\(I=3,5 N\cdot s \)
Qual é a força média exercida pela parede sobre a bola durante uma colisão de duração de 2 segundos, sabendo que uma bola de tênis de 0,3 kg é lançada contra uma parede a uma velocidade de 40 m/s e, após a colisão, ela rebate e sai da parede com uma velocidade de 5 m/s na direção oposta?
A) 3,91 N
B) 4,36 N
C) 5,25 N
D) 6,75 N
Alternativa D.
Calcularemos a força média por meio da fórmula do teorema do impulso e momento linear:
\(I = \Delta p \)
\(F \cdot \Delta t = m\cdot (v_f-v_i) \)
\(F \cdot 2 = 0,3\cdot (40-(-5)) \)
\(F \cdot 2 = 0,3\cdot 45 \)
\(F\cdot 2=13,5 \)
\(F=\frac{13,5}{2 }\)
\(F=6,75 N \)
A respeito dos seus estudos sobre o impulso, responda qual a sua relação com o momento linear.
A) São diretamente proporcionais.
B) São indiretamente proporcionais.
C) São grandezas escalares.
D) Uma é vetorial e a outra escalar.
E) Não estão relacionadas.
Alternativa A.
O momento linear e o impulso são grandezas diretamente proporcionais e vetoriais.
Calcule o impulso a partir dos dados:
- F = 1250 N
- ∆t = 10,7 s
A) 9 841 N·s
B) 11 561 N·s
C) 13 375 N·s
D) 15 826 N·s
E) 17 743 N·s
Alternativa C.
\(I = F \cdot \Delta t \)
\(I = 1250\cdot 10,7 \)
\(I=13 375 N\cdot s \)
A respeito do impulso, qual(is) das proposições informa(m) corretamente a relação entre a grandeza física e a sua unidade de medida?
I. O impulso é medido em Newton por segundo quadrado.
II. A força média é medida em quilograma.
III. O tempo é medido em segundos.
IV. O momento linear é medido em quilograma-metro por segundo.
V. A massa é medida em quilograma por segundo.
Em vista disso, qual das alternativas abaixo está correta?
A) Alternativas I e II.
B) Alternativas III e IV.
C) Alternativas I, III e V.
D) Alternativas II, IV e V.
E) Nenhuma alternativa.
Alternativa B.
I. O impulso é medido em Newton por segundo quadrado. (incorreta)
O impulso é medido em Newton-segundo.
II. A força média é medida em quilograma. (incorreta)
A força média é medida em Newton.
III. O tempo é medido em segundos. (correta)
IV. O momento linear é medido em quilograma-metro por segundo. (correta)
V. A massa é medida em quilograma por segundo. (incorreta)
A massa é medida em quilograma.
