Exercícios sobre lei de Coulomb
(Cesgranrio) A lei de Coulomb afirma que a força de intensidade elétrica de partículas carregadas é proporcional:
I. às cargas das partículas.
II. às massas das partículas.
III. ao quadrado da distância entre as partículas.
IV. à distância entre as partículas.
Das afirmações acima
A) somente I é correta.
B) somente I e III são corretas.
C) somente II e III são corretas.
D) somente II é correta.
E) somente I e IV são corretas.
Alternativa A
De acordo com a lei de Coulomb, a força elétrica é proporcional às cargas elétricas das partículas e inversamente proporcional ao quadrado da distância entre as partículas.
(Unesp) Considere uma experiência em que três cargas pontuais de igual módulo estejam alinhadas e igualmente espaçadas, que as cargas A e C sejam fixas, e que os sinais das cargas A, B e C obedeçam a uma das três configurações seguintes:
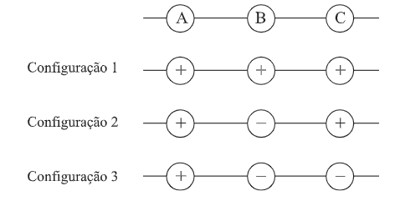
Considere, ainda, que se deseja que a carga B esteja solta e em equilíbrio. Para tanto, das configurações apresentadas, pode-se usar:
A) somente a 1.
B) somente a 2.
C) somente a 3.
D) tanto a 1 quanto a 3.
E) tanto a 1 quanto a 2.
Alternativa E
Para que a carga elétrica B esteja em equilíbrio, é necessário que a resultante das forças elétricas sobre ela seja nula, então, para isso, é necessário que as cargas elétricas A e C sejam iguais, independentemente do sinal da carga elétrica B.
(Mackenzie) Dois corpúsculos eletrizados com cargas elétricas idênticas estão situados no vácuo (\(k_o=9\cdot 10^9\ N m^2 /C^2\)) e distantes 1 m um do outro. A intensidade da força de interação eletrostática entre eles é \(3,6\cdot 10^{-2}\) N. A carga elétrica de cada um desses corpúsculos pode ser (em μC):
A) 9
B) 8
C) 6
D) 4
E) 2
Alternativa E
Calcularemos a carga elétrica desses corpúsculos por meio da lei de Coulomb, dada pela fórmula:
\(F=k_o\cdot \frac{|Q_1 |\cdot |Q_2 |}{d^2 }\)
\(3,6\cdot 10^{-2}=9\cdot 10^{9}\cdot \frac{Q^2}{(1)^2 }\)
\(3,6\cdot 10^{-2}=9\cdot 10^{9}\cdot Q^2\)
\(Q^2=\frac{3,6\cdot 10^{-2}}{9\cdot 10^9}\)
\(Q^2=0,4\cdot 10^{-2-9}\)
\(Q^2=0,4\cdot 10^{-11}\)
\(Q^2=4\cdot 10^{-12}\)
\(Q=\sqrt{4\cdot 10^{-12}}\)
\(Q=2\cdot 10^{-6}\)
\(Q=2\ μC\)
(UEPG - adaptada) A interação eletrostática entre duas cargas elétricas q1 e q2, separadas uma da outra por uma distância r, é F1. A carga q2 é removida e, a uma distância 2r da carga q1, é colocada uma carga q3 cuja intensidade é a terça parte de q2. Nessa nova configuração, a interação eletrostática entre q1 e q3 é F2. Com base nesses dados, assinale o que for correto.
(01) As cargas q1 e q2 têm sinais opostos.
(02) As cargas q2 e q3 têm sinais opostos.
(04) As cargas q1 e q3 têm o mesmo sinal.
(08) A força F2 é repulsiva e a força F1 é atrativa.
(16) A intensidade de F2 = F1/12.
A somatória das alternativas corretas equivale a:
A) 1
B) 6
C) 18
D) 20
E) 31
Alternativa C
(01) As cargas q1 e q2 têm sinais opostos. (Incorreta)
As cargas q1 e q2 têm sinais iguais.
(02) As cargas q2 e q3 têm sinais opostos. (Correta)
(04) As cargas q1 e q3 têm o mesmo sinal. (Incorreta)
As cargas q1 e q3 têm sinais opostos.
(08) A força F2 é repulsiva e a força F1 é atrativa. (Incorreta)
A força F2 é atrativa e a força F1 é repulsiva.
(16) A intensidade de F2 = F1/12. (correta)
Determine a distância entre duas cargas elétricas de módulo \(5\cdot 10^{-3}\ C\) que se repelem no vácuo com uma força elétrica de 20 N.
Dado: \(k_o=9\cdot 10^{9}\ N m^2 /C^2\).
A) 103 m
B) 104 m
C) 105 m
D) 106 m
E) 107 m
Alternativa D
Calcularemos a distância entre essas cargas elétricas por meio da lei de Coulomb, dada pela fórmula:
\(F=k_o\cdot \frac{|Q_1 |\cdot|Q_2 |}{d^2 }\)
\(20=9 \cdot 10^{9}\cdot \frac{5\cdot 10^{-3}\cdot 5\cdot 10^{-3}}{d^2 }\)
\(20=\frac{225\cdot 10^{9-3-3}}{d^2 }\)
\(20=\frac{225\cdot 10^3}{d^2 }\)
\(d^2=\frac{225\cdot 10^3}{20}\)
\(d^2=11,25\cdot 10^3\)
\(d^2=11,25\cdot 1000\)
\(d^2=11.250\)
\(d=\sqrt{11.250}\)
\(d≅106\ m\)
De acordo com a lei de Coulomb, duas cargas elétricas de mesmo sinal apresentam uma força elétrica:
A) repulsiva
B) atrativa
C) nula
D) constante
E) uniforme
Alternativa A
De acordo com a lei de Coulomb, duas cargas elétricas de mesmo sinal apresentam força elétrica repulsiva e cargas elétricas de sinais opostos apresentam força elétrica atrativa.
Dois condutores esféricos com cargas elétricas de 6 C e de 8 C são postos em contato e depois afastados em 2 m. A partir disso, qual é a força elétrica entre essas cargas elétricas após o seu contato?
Dado: \(k_o=9\cdot 10^{9}\ Nm^2/C^2\).
A) \(4,4100\cdot 10^{11}\ N\)
B) \(3,3075\cdot 10^{11}\ N\)
C) \(2,2500\cdot 10^{11}\ N\)
D) \(1,1025\cdot 10^{11}\ N\)
E) zero
Alternativa D
Após o contato entre as cargas elétricas, os seus novos valores são dados pela média aritmética entre as cargas elétricas:
\(\frac{6+8}2=\frac{14}2=7\ C\)
Por fim, calcularemos a força elétrica por meio da lei de Coulomb:
\(F=k_o\cdot \frac{|Q_1 |\cdot |Q_2 |}{d^2 }\)
\(F=9\cdot 10^9\cdot \frac{|7|\cdot |7|}{2^2 }\)
\(F=9\cdot 10^9\cdot \frac{49}4\)
\(F=110,25\cdot 10^9\)
\(F=1,1025\cdot 10^2\cdot 10^9\)
\(F=1,1025\cdot 10^{2+9}\)
\(F=1,1025\cdot 10^{11}\ N\)
Qual a intensidade da força elétrica entre duas cargas elétricas de valor 50 C e –20 C que estão separadas em 100 centímetros no vácuo?
Dado: \(k_o=9\cdot 10^{9}\ Nm^2/C^2\).
A) \(9\cdot 10^{24}\ N\)
B) \(9\cdot 10^{12}\ N\)
C) 0 N
D) \(9\cdot 10^{-12}\ N\)
E) \(9\cdot 10^{-24}\ N\)
Alternativa B
Primeiramente, converteremos a distância de centímetros para metros:
100 cm = 1 m
Por fim, calcularemos a força elétrica por meio da fórmula da lei de Coulomb:
\(F=k_o\cdot \frac{|Q_1 |\cdot |Q_2 |}{d^2 }\)
\(F=9\cdot 10^{9}\frac{|50C|\cdot |-20C|}{(1)^2} \)
\(F=9\cdot 10^9\cdot \frac{50\cdot 20}{1}\)
\(F=9000\cdot 10^9\)
\(F=9\cdot 10^3\cdot 10^9\)
\(F=9\cdot 10^{3+9}\)
\(F=9\cdot 10^{12}\ N\)
Calcule a carga elétrica Q de duas partículas que estão separadas em 50 cm e se atraem com uma força elétrica de 120 N.
Dado: \(k_o=9\cdot 10^9\ N m^2/C^2\).
A) \(- 5,77\cdot 10^{-5}\ C\) e \(- 5,77\cdot 10^{-5}\ C\)
B) \(+ 5,77\cdot 10^{-5}\ C\) e \(- 5,77\cdot 10^{-5}\ C\)
C) \(+ 5,77\cdot 10^{-5}\ C\) e \(+ 5,77\cdot 10^{-5}\ C\)
D) \(+ 5,77\cdot 10^{-5}\ C\) e 0 C
E) \(- 5,77\cdot 10^{-5}\ C\) e 0 C
Alternativa B
Primeiramente, converteremos a distância de centímetros para metros:
50 cm = 0,5 m
Por fim, calcularemos as cargas elétricas por meio da fórmula da lei de Coulomb:
\(F=k_o\cdot \frac{|Q_1 | \cdot |Q_2 |}{d^2 }\)
\(F=k_o\cdot \frac{|Q|\cdot |Q|}{d^2 }\)
\(120=9\cdot 10^9\cdot \frac{Q^2}{0,5^2} \)
\(120=9\cdot 10^9\cdot \frac{Q^2}{0,25} \)
\(Q^2=\frac{120\cdot 0,25}{9\cdot 10^9}\)
\(Q^2=\frac{30}{9\cdot 10^9}\)
\(Q^2≈3,333\cdot 10^{-9}\)
\(Q=\sqrt{3,333\cdot 10^{-9}}\)
\(Q≈± 5,77\cdot 10^{-5}\ C\)
Como as partículas se atraem, uma delas apresenta uma carga elétrica de \(5,77\cdot 10^{-5}\ C\) e a outra apresenta uma carga elétrica de \(-5,77\cdot 10^{-5}\ C\).
Uma carga elétrica q e outra carga elétrica 2 q, inicialmente a uma distância d, são separadas até uma distância 2 d, com isso, determine a força elétrica final em termos da força elétrica inicial.
A) \(F_{final}=\frac{F_{inicial}}8\)
B) \( F_{final}=8\cdot F_{inicial}\)
C) \(F_{final}=\frac{F_{inicial}}4\)
D) \( F_{final}=F_{inicial}\)
E) \( F_{final}=4\cdot F_{inicial}\)
Alternativa C
Para determinarmos a força elétrica final em termos da força elétrica inicial, faremos uma comparação entre a força elétrica final e a força elétrica inicial por meio da fórmula da lei de Coulomb:
\(F=k_o\cdot \frac{|Q_1 |\cdot |Q_2 |}{d^2 }\)
A força elétrica inicial é de:
\(F_{inicial}=k_o\cdot \frac{|Q_1 |\cdot |Q_2 |}{d_{inicial}^2}\)
\(F_{inicial}=k_o\cdot \frac{|q |\cdot |2q|}{d^2}\)
\(F_{inicial}=k_o\cdot \frac{2\cdot q^2}{d^2}\)
Já a força elétrica final mede:
\(F_{final}=k_o\cdot \frac{|Q_1 |\cdot |Q_2 |}{d_{final}^2}\)
\(F_{final}=k_o\cdot \frac{|q|\cdot |2q|}{(2d^2)} \)
\(F_{final}=k_o\cdot \frac{2\cdot q^2}{4\cdot d^2}\)
Então a força elétrica final em termos da força elétrica inicial é:
\(F_{final}=\frac{1}4 \cdot k_o\cdot \frac{2\cdot q^2}{d^2} \)
Substituindo pela força inicial:
\(F_{final}=\frac{1}4\cdot F_{inicial}\)
\(F_{final}=\frac{F_{inicial}}4\)
Duas cargas elétricas de mesmo módulo 0,04 C se atraem no vácuo com uma força elétrica de 1200 N. Com base nisso, calcule a distância aproximada delas.
Dado: \(k_o=9 \cdot 10^9\ N m^2/C^2\).
A) \(0,236\cdot 10^2\ m\)
B) \(1,095\cdot 10^2\ m\)
C) \(2,547\cdot 10^2\ m\)
D) \(3,958\cdot 10^2\ m\)
E) \(4,621\cdot 10^2\ m\)
Alternativa B
Calcularemos a distância entre as cargas elétricas por meio da lei de Coulomb:
\(F=k_o\cdot \frac{|Q_1 |\cdot |Q_2 |}{d^2 }\)
\(1200=9\cdot 10^{9} \cdot \frac{0,04 \cdot 0,04}{d^2 }\)
\(1200=9\cdot 10^9 \cdot \frac{0,0016}{d^2 }\)
\(1200=\frac{0,0144\cdot 10^9}{d^2 }\)
\(d^2=\frac{0,0144\cdot 10^9 }{1200}\)
\(d^2=0,000012\cdot 10^9 \)
\(d^2=1,2\cdot 10^{-5}\cdot 10^9 \)
\(d^2=1,2\cdot 10^{-5+9}\)
\(d^2=1,2\cdot 10^4 \)
\(d=\sqrt{1,2\cdot10^4}\)
\(d≈1,095\cdot 10^2\ m \)
Qual(is) das alternativa(s) apresentam a unidade de medida correspondente à grandeza física estudada na energia potencial elétrica:
I. O campo elétrico é medido em Newton por Coulomb.
II. A carga elétrica é medida em Coulomb.
III. A força elétrica é medida em Newton por Joule.
IV. A distância é medida em metros.
Está(ão) correta(s):
A) I e II.
B) III e IV.
C) I e IV.
D) II e III.
E) I, II e IV.
Alternativa E
I. O campo elétrico é medido em Newton por Coulomb. (Correta)
II. A carga elétrica é medida em Coulomb. (Correta)
III. A força elétrica é medida em Newton por Joule. (Incorreta)
A unidade de medida da força elétrica é o Newton.
IV. A distância é medida em metros. (Correta)
