Exercícios sobre máquinas térmicas
(ITA) Uma máquina térmica opera segundo o ciclo JKLMJ mostrado no diagrama T-S da figura.
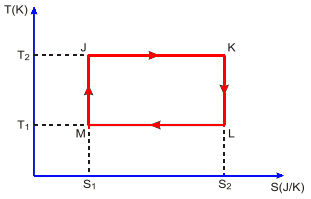
Pode-se afirmar que
a) processo JK corresponde a uma compressão isotérmica.
b) o trabalho realizado pela máquina em um ciclo é W = (T2 – T1)(S2 – S1).
c) o rendimento da máquina é dado por η = 1 – T2/T1
d) durante o processo LM, uma quantidade de calor QLM = T1(S2 – S1) é absorvida pelo sistema.
e) outra máquina térmica que opere entre T2 e T1 poderia eventualmente possuir um rendimento maior que a desta.
LETRA “B”
O gráfico dado na questão é de temperatura versus entropia e mostra um ciclo no sentido horário operado por uma máquina térmica.
A) ERRADO: No processo JK, há aumento de entropia (S2 > S1), o que indica que o sistema recebeu calor, logo, realizou trabalho.
B) CORRETO: O trabalho de um sistema cíclico é dado pela área da figura geométrica que forma o ciclo. Nesse caso, a área de um retângulo (base x altura).
c) ERRADO: A razão das temperaturas para o cálculo do rendimento é entre a menor e maior temperatura. Nesse caso, teríamos η = 1 – T1/T2 já que T1 < T2.
d) ERRADO: Durante o processo LM, há diminuição de entropia, o que indica perda de calor.
e) ERRADO: Outra máquina operando sob o mesmo ciclo realizaria o mesmo trabalho.
Uma máquina térmica que trabalha entre as temperaturas 27°C e 327°C possui 80% do rendimento ideal para uma máquina térmica. Se essa máquina recebe 1000 J da fonte quente, qual é o trabalho realizado por ela?
a) 400 J
b) 500 J
c) 350 J
d) 600 J
e) 250 J
LETRA “A”
Transformação de temperaturas: As temperaturas devem sempre estar expressas em K. Como TK = TC + 273, sendo TK a temperatura em Kelvin e TC a temperatura em °C, temos:
27 + 273 = 300 K
327 + 273 = 600 K
O rendimento ideal citado na questão refere-se ao ciclo de Carnot, logo, temos:
η I = 1 – T2/T1
Para essa equação, podemos escrever que:
η I = Rendimento ideal;
T2 = Temperatura da fonte fria;
T1 = Temperatura da fonte quente.
η I = 1 – 300/600
η I = 1 – 0,5
η I = 0,5
O rendimento real da máquina η R corresponde a 80% do rendimento ideal η I , logo:
η R = 80% η I
η R = 0,8. 0,5
η I =0,8 x 0,5
η I = 0,4 ou 40 %
Sendo o rendimento a razão entre o trabalho e o calor fornecido (Q1), temos:
η I = τ ÷ Q1
0,4 = τ ÷ 1000
τ = 400 J
Determine o trabalho realizado por uma máquina de Carnot que recebe 2000 J de calor de uma fonte quente e trabalha sob as temperaturas de 400 K e 700 K.
a) 1000 J
b) 780 J
c) 800 J
d) 860 J
e) 560 J
LETRA “D”
A partir do rendimento para uma máquina de Carnot, temos:
η = 1 – T2/T1
η = 1 – 400/700
η = 1 – 0,57
η = 0,43 ou 43 %
Sendo o rendimento a razão entre o trabalho e o calor fornecido (Q1), temos:
η = τ ÷ Q1
0,43 = τ ÷ 2000
τ = 2000. 0,43 = 860 J
(CEFET-PR) O 2° princípio da Termodinâmica pode ser enunciado da seguinte forma: "É impossível construir uma máquina térmica operando em ciclos, cujo único efeito seja retirar calor de uma fonte e convertê-lo integralmente em trabalho." Por extensão, esse princípio nos leva a concluir que:
a) sempre se pode construir máquinas térmicas cujo rendimento seja 100%;
b) qualquer máquina térmica necessita apenas de uma fonte quente;
c) calor e trabalho não são grandezas homogêneas;
d) qualquer máquina térmica retira calor de uma fonte quente e rejeita parte desse calor para uma fonte fria;
e) somente com uma fonte fria, mantida sempre a 0°C, seria possível a uma certa máquina térmica converter integralmente calor em trabalho.
LETRA “D”
Qualquer máquina térmica, ao receber calor, executa a sua função (trabalho) e perde calor para uma fonte fria.
