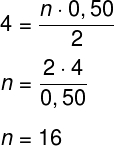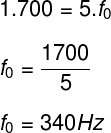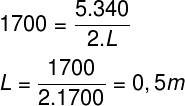Exercícios sobre ondas estacionárias em cordas
Sobre uma corda vibrante de 2 m de comprimento é formada uma onda estacionária correspondente ao primeiro harmônico (frequência fundamental). O comprimento de onda dessa oscilação tem módulo igual a:
a) 4,0 m;
b) 2,0 m;
c) 1,0 m;
d) 0,5 m;
e) 8,0 m.
Letra A
Para que um harmônico seja formado em uma corda vibrante, é necessário que os nós da onda estacionária estejam nas extremidades da corda. Dessa forma, existe uma relação entre o comprimento da corda e o comprimento de onda do harmônico:
Na equação acima, L é o comprimento da corda, n é a ordem do harmônico (n = 1,2,3...), e λ é o comprimento da onda estacionária que se forma na corda. O exercício referiu-se à formação do primeiro harmônico, portanto, o valor de n é 1. Dessa forma, temos que:
Multiplicando os termos, encontramos um valor de λ = 4 m para o harmônico fundamental.
Uma onda estacionária cujo comprimento de onda mede 50 cm é formada em uma corda vibrante de 4,0 m de comprimento. A ordem do harmônico formado é igual a:
a) 8
b) 12
c) 16
d) 4
e) 2
Letra C
A relação entre o comprimento da corda e o comprimento da onda estacionária é determinada pela equação a seguir:
Sendo o comprimento da corda 4,0 m e o comprimento da onda (λ) igual a 0,5 m (50 cm = 0,5 m), escrevemos que:
Portanto, o harmônico formado na corda corresponde ao décimo sexto harmônico (n = 16).
(UCS-Adaptado) Um tubo sonoro aberto emite o seu quinto harmônico com frequência de 1,7kHz. A velocidade do som, no ar que preenche o tubo, tem módulo igual a 340 m/s. O comprimento do tubo vale:
a) 5,0 m
b) 0,5 m
c) 0,25 m
d) 0,025 m
e) 2,0 m
Letra B
Dessa forma, a frequência do 5º harmônico (1,7 kHz = 1700 Hz) é 5 vezes a frequência fundamental:
Relacionando o comprimento de onda formado no tubo com o seu comprimento e a velocidade do som, podemos usar a seguinte expressão:
Utilizando as informações dadas pelo enunciado do exercício, temos que:
Portanto, o comprimento desse tubo sonoro é de 0,5 m.
Em uma corda vibrante, forma-se uma onda estacionária correspondente ao quinto harmônico. O número de meio comprimento de onda e o de nós nessa corda equivalem a, respectivamente:
a) 4 e 5
b) 5 e 4
c) 6 e 5
d) 5 e 6
e) 2 e 3
Letra D
A relação entre o comprimento de uma corda e a ordem do harmônico formado sobre ela é dada por:
Dessa forma, n (a ordem do harmônico) corresponde à quantidade de meio comprimento de onda, que totaliza o comprimento total da corda vibrante, e o número de nós é sempre igual a (n+1), ou seja, o número do harmônico acrescido de 1. Portanto, o número de meio comprimento de onda é 5, enquanto o número de nós é 6.