Exercícios sobre Plano inclinado com atrito
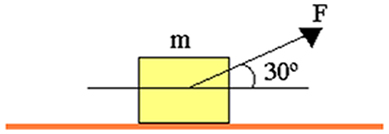
Vamos supor que temos um bloco de massa m = 5 kg sobre uma superfície plana. Suponhamos que o coeficiente de atrito entre o bloco e a superfície plana seja igual a 0,2, determine o valor da força de atrito para uma força que puxa o bloco com intensidade igual a 50 N.
a) 5 N
b) 10 N
c) 50 N
d) 0
e) 100 N
Primeiramente devemos retirar os dados do problema
m=5 kg;F=50 N; μ=0,2; θ=30°
Como sabemos que a força faz um ângulo de 30° com a horizontal, devemos decompor a força na direção y (Fy = F.sen30°), pois a força de atrito depende da normal e do coeficiente de atrito, assim temos:
fat = μ.N
N = P- Fy
N=m.g - F.sen30°
N=5 .10- 50 .0,5
N= 25 N
Substituindo o valor da normal na equação da força de atrito, temos:
fat = 0,2 .25
fat = 5N
Alternativa A
(UFLA-MG) Um bloco de gelo desprende-se de uma geleira e desce um plano inclinado com atrito. Qual o diagrama que representa corretamente as forças que atuam sobre o bloco?
a)
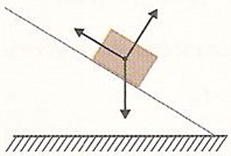
b)
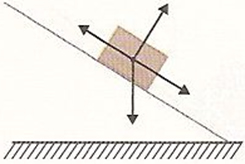
c)
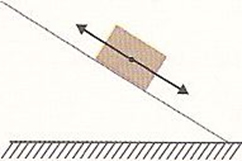
d)
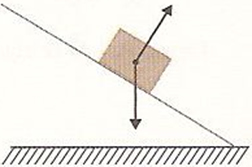
e)
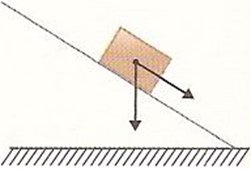
Como o bloco desce um plano inclinado feito de gelo, não podemos desprezar o atrito entre o bloco de gelo e a superfície, por mais lisa que seja ainda sim existe atrito. Sendo assim, temos atuando no bloco de gelo as seguintes forças: normal, força de atrito (contrária ao movimento do bloco) e a força peso.
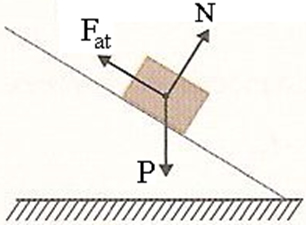
Alternativa A
(UNIFOR CE) Um bloco de massa de 4,0 kg é abandonado num plano inclinado de 37º com a horizontal com o qual tem coeficiente de atrito 0,25. A aceleração do movimento do bloco é em m/s2. Dados: g = 10 m/s2; sen 37º = 0,60; cos 37º = 0,80.
a) 2,0
b) 4,0
c) 6,0
d) 8,0
e) 10
Como o exercício diz respeito a um plano inclinado, primeiramente devemos representa-lo através de um desenho, em seguida representar as forças que atuam no bloco e, por fim, calcular o que se pede.
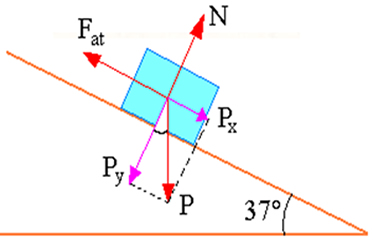
A figura acima representa as forças que estão atuando sobre o corpo. Como o exercício nos pede a aceleração com que o bloco desce o plano inclinado, iremos usar a segunda Lei de Newton para descobrir a aceleração do bloco. Assim, temos:
FR=m.a
Px-Fat=m.a
Como:
Px = P.sen37° ; Fat = μ.N; N = P.cos37°
Temos:
P.sen37°-μ.P.cos37°=m.a
40 .0,6-0,25 .40 .0,8=4a
4a=24-8
.jpg)
Alternativa B
Vejamos a figura abaixo. Nela temos a representação de diversas forças que agem sobre o bloco sobre um plano inclinado. O vetor que melhor representa a força peso do bloco é:
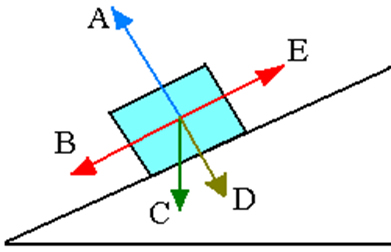
a) A
b) B
c) C
d) D
e) E
Como sabemos, a força peso sempre tem direção que aponta para o centro da Terra, portanto a força que melhor representa a força peso atuando no bloco é a letra C, cuja direção é vertical para baixo.
