Exercícios sobre resistividade elétrica
(Enem) A resistência elétrica de um fio é determinada pelas suas dimensões e pelas propriedades estruturais do material. A condutividade (σ) caracteriza a estrutura do material, de tal forma que a resistência de um fio pode ser determinada conhecendo-se L (comprimento do fio) e A (a área de seção reta). A tabela relaciona o material à sua respectiva resistividade em temperatura ambiente.
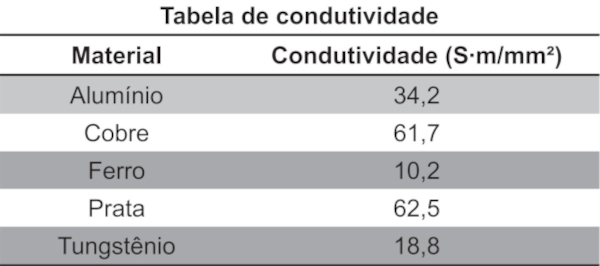
Mantendo-se as mesmas dimensões geométricas, o fio que apresenta menor resistência elétrica é aquele feito de:
A) tungstênio.
B) alumínio.
C) ferro.
D) cobre.
E) prata.
Alternativa E.
Quanto menor for a resistência elétrica de um fio, menor será a sua resistividade elétrica e, consequentemente, maior será a sua condutividade elétrica. Assim, o fio que apresenta a menor resistência elétrica é a prata.
(Famec) Considerem-se dois fios condutores do mesmo material: o primeiro com diâmetro igual a 0,6 mm, comprimento 6 m e resistência 12 Ω e o segundo com diâmetro igual a 0,4 mm, comprimento igual a 4 m e resistência igual a . Com base nessas informações, conclui-se que xΩ é igual a:
A) 6
B) 8
C) 10
D) 12
E) 18
Alternativa E.
Primeiramente, transformaremos os diâmetros de milímetros para metros:
\(0,6 mm= 0,0006 m\)
\(0,4 mm= 0,0004 m\)
Depois, calcularemos as áreas de secção transversal dos fios condutores através da sua fórmula:
\(A_{r_1} = \pi \cdot r_{r_1}^{2} \)
\(A_{r_1} = \pi \cdot \left(\frac{d_{r_1}}{2}\right)^{2} \)
\(A_{r_1} = \pi \cdot \left(\frac{0,0006}{2}\right)^{2} \)
\(\)\(A_{r_1} = \pi \cdot \left(0,0003\right)^{2} \)
\(A_{r_1} = \pi \cdot 9 \cdot 10^{-8} \, \text{m}^{2} \)
\(A_{r_2} = \pi \cdot r_{r_2}^{2} \)
\(A_{r_2} = \pi \cdot \left(\frac{d_{r_2}}{2}\right)^{2} \)
\(A_{r_2} = \pi \cdot \left(\frac{0,0004}{2}\right)^{2} \)
\(A_{r_2} = \pi \cdot \left(0,0002\right)^{2} \)
\(A_{r_2} = \pi \cdot 4 \cdot 10^{-8} \, \text{m}^{2} \)
Em seguida, calcularemos a resistividade elétrica do fio 1 através da sua fórmula:
\(\rho_{1} = \frac{R_{1} \cdot A_{1}}{L_{1}} \)
\(\rho_{1} = \frac{12 \cdot \pi \cdot 9 \cdot 10^{-8}}{6} \)
\(\rho_{1} = \pi \cdot 1,8 \cdot 10^{-7} \, \Omega \cdot \text{m} \)
Por fim, como os materiais são os mesmos, a resistividade elétrica é a mesma, então:
\(\rho_{2} = \frac{R_{2} \cdot A_{2}}{L_{2}} \)
\(\pi \cdot 1,8 \cdot 10^{-7} = \frac{R_{2} \cdot \pi \cdot 4 \cdot 10^{-8}}{4} \)
\(R_{2} = \frac{4 \cdot \pi \cdot 1,8 \cdot 10^{-7}}{\pi \cdot 4 \cdot 10^{-8}} \)
\(R_{2} = \frac{1,8 \cdot 10^{-7}}{10^{-8}} \)
\(R_{2} = 1,8 \cdot 10^{-7+8} \)
\(R_{2} = 1,8 \cdot 10^{1} \)
\(R = 18 Ω\)
(Mackenzie) Dois resistores, de resistências elétricas R1 e R2, são formados por fios metálicos, de mesmo comprimento e mesmo diâmetro, e são constituídos de materiais cujas resistividades são ρ1 e ρ2 respectivamente. Quando esses resistores são associados em paralelo e submetidos a uma bateria de tensão elétrica U, a corrente que passa pelo fio de resistência elétrica R2 é o dobro da que passa por R1. Nessas condições, a relação entre as resistividades dos materiais é
A) ρ1 = ρ2
B) ρ2 = 2. ρ1
C) ρ1 = 2. ρ2
D) ρ1 = 4. ρ2
E) ρ2 = 4. ρ1
Alternativa C.
De acordo com o enunciado, quando os fios estão submetidos à mesma tensão elétrica, a corrente elétrica que passa no fio 2 é o dobro da corrente elétrica que passa no fio 1, então, igualaremos as tensões elétricas e substituiremos pela fórmula da 1ª lei de Ohm:
\(U_1 = U_2 \)
\(R_1 \cdot i_1 = R_2 \cdot i_2 \)
\(R_1 \cdot i_1 = R_2 \cdot 2 \cdot i_2\)
\(R_1 = R_2 \cdot 2 \)
Depois, isolaremos o termo da resistência elétrica na fórmula da resistividade elétrica:
\(R = \frac{\rho \cdot L}{A} \)
Em seguida, substituiremos na relação obtida anteriormente:
\(R_1 = R_2 \cdot 2 \)
\(\frac{{\rho_1 \cdot L_1}}{{A_1}} = \frac{{\rho_2 \cdot L_2}}{{A_2}} \cdot 2 \)
Como o comprimento e o diâmetro são iguais, podemos eliminá-los:
\(\rho_{1} = \rho_{2} \cdot 2 \)
A partir dos seus estudos a respeito da resistividade elétrica, responda a seguinte pergunta: Quais são os fatores que influenciam na resistividade elétrica?
I. Comprimento.
II. Resistência elétrica.
III. Campo magnético.
IV. Área da secção transversal.
A) Alternativas I, II e III.
B) Alternativas II, III e IV.
C) Alternativas I, III e IV.
D) Alternativas I, II e IV.
E) Todas estão corretas.
Alternativa D.
O campo magnético não influência na resistividade elétrica do material, apenas o comprimento, a área de secção transversal e a resistência elétrica do condutor.
Determine a área de secção transversal de um condutor de 0,8 metros que possui resistência elétrica de \(0,0006 Ω\) e resistividade elétrica de \(2,5\cdot {10} ^ {-3} Ω \cdot m\).
A) \(3,34 {m} ^ {2}\)
B) \(4,48 {m} ^ {2}\)
C) \( 5,96 {m} ^ {2}\)
D) \(6,13 {m} ^ {2}\)
E) \(7,82 {m} ^ {2}\)
Alternativa A.
Calcularemos a área de secção transversal do condutor a partir da fórmula da resistividade elétrica:
\(\rho = \frac{R \cdot A}{L} \)
\(2,5 \cdot 10^{-3} = \frac{0,0006 \cdot A}{0,8} \)
\(A = \frac{2,5 \cdot 10^{-3} \cdot 0,8}{0,0006} \)
\(A = \frac{0,0025 \cdot 0,8}{0,0006} \)
\(A ≅ 3,34 {m} ^ {2}\)
Calcule a resistividade elétrica de um condutor X com resistência elétrica de \(0,04 Ω\), com área transversal de \(0,16 {m} ^ {2}\) e com comprimento de 2 m.
A) 0,0016 Ω ∙ m
B) 0,0032 Ω ∙ m
C) 0,0048 Ω ∙ m
D) 0,0064 Ω ∙ m
E) 0,0080 Ω ∙ m
Alternativa B.
Calcularemos a resistividade elétrica a partir da sua fórmula:
\(\rho = \frac{R \cdot A}{L} \)
\(\rho = \frac{0,04 \cdot 0,16}{2} \)
\(ρ =0,0032 Ω \cdot m \)
Um condutor tem resistividade elétrica de 300 Ω∙ m, comprimento de 5 metros e área de secção transversal de \(0,3 {m} ^ {2}\). Com base nessas informações, qual é a resistência elétrica desse condutor?
A) \( 3\cdot{10} ^ {3} Ω\)
B) \(4\cdot {10} ^ {3} Ω\)
C) \(5 \cdot {10} ^ {3} Ω\)
D) \(6\cdot {10} ^ {3} Ω\)
E) \(7\cdot {10} ^ {3} Ω\)
Alternativa C.
Calcularemos a resistência elétrica através da fórmula da resistividade elétrica:
\(\rho = \frac{R \cdot A}{L} \)
\(300 = \frac{R \cdot 0,3}{5} \)
\(R = \frac{300 \cdot 5}{0,3} \)
\(R =5000\)
\(R =5 \cdot {10} ^ {3} Ω\)
Sabendo que a resistência elétrica, a área de secção transversal e a resistividade elétrica de um fio de ferro são \(3\cdot {10} ^ {-3} Ω\), 0,5m e \(2\cdot {10} ^ {-7} Ω \cdot m\), respectivamente, determine o seu comprimento.
A) 5500 m
B) 6000 m
C) 6500 m
D) 7000 m
E) 7500 m
Alternativa E.
Calcularemos o comprimento do fio através da fórmula da resistividade elétrica:
\(\rho = \frac{R \cdot A}{L} \)
\(2 \cdot 10^{-7} = \frac{3 \cdot 10^{-3} \cdot 0,5}{L} \)
\(L = \frac{3 \cdot 10^{-3} \cdot 0,5}{2 \cdot 10^{-7}} \)
\(L = 0,75 \cdot 10^{-3+7} \)
\(L = 7,5 \cdot 10^{-1-3+7} \)
\(L = 7,5 \cdot 10^{3} \text{ m} \)
\(L =7500 m\)
Um condutor de 4 metros de comprimento e \({10} ^ {-2}\) metros de área transversal apresenta uma resistência elétrica de \(0,0005 Ω\). Determine sua resistividade elétrica.
A) \(0,25 \cdot 10^{-6} \, \Omega \cdot \text{m} \)
B) \(0,50 \cdot 10^{-6} \, \Omega \cdot \text{m} \)
C) \(0,87 \cdot 10^{-6} \, \Omega \cdot \text{m} \)
D) \(1,25 \cdot 10^{-6} \, \Omega \cdot \text{m} \)
E) \(1,50 \cdot 10^{-6} \, \Omega \cdot \text{m} \)
Alternativa D.
Calcularemos a resistividade elétrica a partir da sua fórmula:
\(\rho = \frac{R \cdot A}{L} \)
\(\rho = \frac{0,0005 \cdot 10^{-2}}{4} \)
\(\rho = \frac{0,0005 \cdot 10^{-2}}{4} \)
\(ρ =0,00000125\)
\(\rho = 1,25 \times 10^{-6} \, \Omega \cdot \text{m} \)
Calcule a resistividade elétrica de um condutor formado por um material com condutividade elétrica de \(1 \cdot 10^{4} \, \Omega \cdot \text{m}^{-1} \).
A) \(1 \cdot 10^{-4} \, \Omega \cdot \text{m} \)
B) \(1 \cdot 10^{-5} \, \Omega \cdot \text{m} \)
C) \(1 \cdot 10^{-6} \, \Omega \cdot \text{m} \)
D) \(1 \cdot 10^{-7} \, \Omega \cdot \text{m} \)
E) \(1 \cdot 10^{-8} \, \Omega \cdot \text{m} \)
Alternativa A.
Calcularemos a resistividade elétrica do material através da fórmula que a relaciona com a condutividade elétrica:
\(\rho = \frac{1}{\sigma} \)
\(\rho = \frac{1}{1 \cdot 10^{4}} \)
\(\rho = \frac{1}{10 000} \)
\(\rho = 0,0001 \)
\(\rho = 1 \cdot 10^{-4} \, \Omega \cdot \text{m} \)
Um condutor de comprimento L, resistência elétrica R, área de secção transversal A e resistividade elétrica ρ é fragmentado em três partes, mantendo constante sua resistência elétrica e sua área de secção transversal. O que a resistividade elétrica de um desses fragmentos será em relação à resistividade elétrica original?
A) O dobro.
B) O triplo.
C) O mesmo.
D) A metade.
E) O quádruplo.
Alternativa B.
Inicialmente, a resistividade elétrica do condutor será:
\(\rho = \frac{R \cdot A}{L} \)
Após a fragmentação, o seu comprimento é dividido em três partes, então, a nova resistividade elétrica é:
\(\rho' = \frac{R \cdot A}{\frac{L}{3}} \)
\(\rho' = 3 \cdot \frac{R \cdot A}{L} \)
\(\rho' = 3 \cdot \rho \)
Quais das alternativas a seguir apresentam as unidades de medidas correspondentes às grandezas físicas estudadas na resistividade elétrica?
I. A resistividade elétrica é medida em Ohm-metro.
II. A resistência elétrica é medida em Ohm.
III. A área de secção transversal do condutor é medida em metros.
IV. O comprimento do condutor é medido em metros quadrados.
V. A condutividade elétrica é medida em Ohm-metro.
A) Alternativas I e II.
B) Alternativas III e IV.
C) Alternativas I e V.
D) Alternativas II e III.
E) Alternativas II e IV.
Alternativa A.
I. A resistividade elétrica é medida em Ohm-metro. (correta)
II. A resistência elétrica é medida em Ohm. (correta)
III. A área de secção transversal do condutor é medida em metros. (incorreta)
A área de secção transversal do condutor é medida em metros quadrados
IV. O comprimento do condutor é medido em metros quadrados. (incorreta)
O comprimento do condutor é medido em metros.
V. A condutividade elétrica é medida em Ohm-metro. (incorreta)
A condutividade elétrica é medida em \({[ Ω\cdot m ]} ^ {-1}\).
