Exercícios sobre segunda lei de Kepler
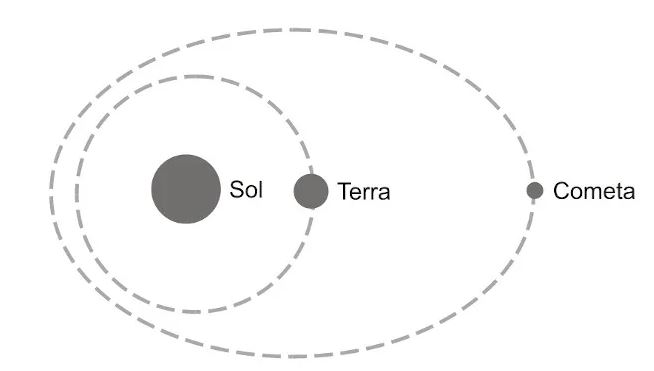
(UFSM) Os avanços nas técnicas observacionais têm permitido aos astrônomos rastrear um número crescente de objetos celestes que orbitam o Sol. A figura mostra, em escala arbitrária, as órbitas da Terra e de um cometa (os tamanhos dos corpos não estão em escala). Com base na figura, analise as afirmações:
I. Dada a grande diferença entre as massas do Sol e do cometa, a atração gravitacional exercida pelo cometa sobre o Sol é muito menor que a atração exercida pelo Sol sobre o cometa.
II. O módulo da velocidade do cometa é constante em todos os pontos da órbita.
III. O período de translação do cometa é maior que um ano terrestre.
Está(ão) correta(s):
a) apenas I
b) apenas III
c) apenas I e II
d) apenas II e III
e) I, II e III
Letra B
I – Incorreta. Dada a grande diferença entre as massas do Sol e do cometa, a atração gravitacional exercida pelo cometa sobre o Sol é a mesma que a atração exercida pelo Sol sobre o cometa.
II –Incorreta. O módulo da velocidade do cometa não é constante em todos os pontos da órbita.
III – Correta.
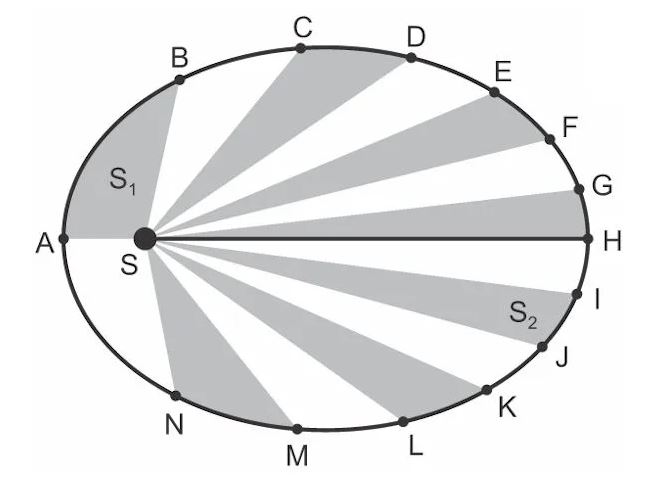
(UFRGS) A elipse, na figura abaixo, representa a órbita de um planeta em torno de uma estrela S. Os pontos ao longo da elipse representam posições sucessivas do planeta, separadas por intervalos de tempo iguais. As regiões alternadamente coloridas representam as áreas varridas pelo raio da trajetória nesses intervalos de tempo. Na figura, em que as dimensões dos astros e o tamanho da órbita não estão em escala, o segmento de reta SH representa o raio focal do ponto H, de comprimento p.
Considerando que a única força atuante no sistema estrela-planeta seja a força gravitacional, são feitas as seguintes afirmações:
I. As áreas S1 e S2, varridas pelo raio da trajetória, são iguais.
II. O período da órbita é proporcional a p3.
III. As velocidades tangenciais do planeta nos pontos A e H, VA e VH são tais que VA > VH.
Quais estão corretas?
a) Apenas I
b) Apenas I e II
c) Apenas I e III
d) Apenas II e III
e) I, II e III
Letra C.
I – Correta.
II – Incorreta. O período da órbita é proporcional ao cubo do raio médio.
III – Correta.
(UFPG) Aproximadamente durante um período de quase 2000 anos, a humanidade aceitou a teoria geocêntrica, isto é, a Terra como centro do Universo. Graças ao trabalho de grandes cientistas, entre eles Johannes Kepler, estabeleceu-se a verdade em relação ao Sistema Solar: a teoria heliocêntrica tendo o Sol como o centro do Sistema Solar e os planetas girando ao seu redor. Com relação às leis enunciadas por Kepler, assinale a alternativa correta.
a) Um planeta em órbita em torno do Sol não se move com velocidade constante, mas de tal maneira que uma linha traçada do planeta ao Sol varre áreas iguais em intervalos de tempo iguais.
b) Todos os planetas do Sistema Solar, incluindo a Terra, giram em torno do Sol em órbitas circulares, tendo o Sol como centro.
c) Periélio é a aproximação entre os planetas e o Sol, enquanto afélio é o afastamento entre os planetas e o Sol. No inverno ocorre o periélio.
d) A segunda lei de Kepler prova que a maior velocidade de translação dos planetas, no periélio, é menor que nos pontos mais afastados, no afélio.
e) As leis enunciadas por Kepler são válidas apenas para o Sistema Solar.
Letra A
A) Correta.
B) Incorreta. Todos os planetas do Sistema Solar, incluindo a Terra, giram em torno do Sol em órbitas elípticas.
C) Incorreta. Periélio é a aproximação entre os planetas e o Sol, enquanto afélio é o afastamento entre os planetas e o Sol. O periélio e afélio não têm relação com as estações do ano.
D) Incorreta. A segunda lei de Kepler prova que a maior velocidade de translação dos planetas é no periélio e é menor nos pontos mais afastados, no afélio.
E) Incorreta. As leis enunciadas por Kepler são válidas não só apenas para o Sistema Solar.
(Mackenzie-SP) De acordo com uma das leis de Kepler, cada planeta completa (varre) áreas iguais em tempos iguais em torno do Sol.
Como as órbitas são elípticas, e o Sol ocupa um dos focos, conclui-se que:
I - Quando o planeta está mais próximo do Sol, sua velocidade aumenta.
II - Quando o planeta está mais distante do Sol, sua velocidade aumenta.
III - A velocidade do planeta em sua órbita elíptica independe de sua posição relativa ao Sol.
Responda de acordo com o código a seguir:
a) Somente I é correta.
b) Somente II é correta.
c) Somente II e III são corretas
d) Todas são corretas
e) Nenhuma é correta.
Letra A
I – Correta.
II – Incorreta. Quando o planeta está mais perto do Sol, sua velocidade aumenta.
III – Incorreta. A velocidade do planeta em sua orbita elíptica depende de sua posição relativa ao Sol.
As posições do periélio e afélio são de:
a) maior e menor energia potencial gravitacional.
b) maior e menor velocidade orbital.
c) maior velocidade orbital.
d) menor velocidade orbital.
e) maior energia potencial gravitacional.
Letra B
A posição do planeta no periélio faz com que sua velocidade orbital seja maior. Já na posição do afélio, ele possui menor velocidade orbital.
De acordo com o que foi estudado na segunda lei de Kepler, é verdadeiro afirmar que:
a) o cubo do raio médio das órbitas é proporcional ao quadrado do período orbital.
b) o cubo do raio médio das órbitas é inversamente proporcional ao quadrado do período orbital.
c) o tempo para percorrer a área 1 será o mesmo para percorrer a área 2.
d) o tempo para percorrer a área 1 é diferente do tempo para percorrer a área 2.
e) todas são falsas.
Letra C
De acordo com a segunda lei de Kepler, o tempo para percorrer a área 1 será o mesmo para percorrer a área 2.
A Terra dá a volta em torno do Sol, cuja área é de 6,98∙1022m2 . Qual é a área varrida pelo raio que liga a Terra ao Sol durante um dia, contando de 0h do dia 20 de março até 24h do dia 20 de maio do próximo ano?
a) \(A_2\approx5,16333\bullet{10}^{22}\)
b) \(A_2\approx4,16333\bullet{10}^{22}\)
c) \(A_2\approx3,16333\bullet{10}^{22}\)
d) \(A_2\approx2,16333\bullet{10}^{22}\)
e) \(A_2\approx1,16333\bullet{10}^{22}\)
Letra E
Utilizando a fórmula da segunda lei de Kepler:
\(\frac {A_{1}} {∆t_{1}}=\frac {A_{2}}{∆t_{2}}\)
∆t1 é o tempo que a Terra demora para dar uma volta ao redor do Sol, e ∆t2 é o tempo entre 0h do dia 20 de março até as 24h do dia 20 de maio do próximo ano.
\(\frac{6,98\bullet{10}^{22}}{12}=\frac{A_2}{2}\)
\(A_2=\frac{2\bullet6,98\bullet{10}^{22}}{12}\)
\(A_2\approx1,16333\bullet{10}^{22}\)
Um satélite se movendo ao redor da Terra descreveu uma área de 20 mil km2 em 2 horas. Quanto tempo ele demorará para descrever uma área de 50 mil km2 ?
a) 8 horas
b) 2 horas
c) 10 horas
d) 5 horas
e) 4 horas
Letra D
Utilizando a fórmula da segunda lei de Kepler:
\(\frac {A_{1}} {∆t_{1}}=\frac {A_{2}}{∆t_{2}}\)
\(\frac{{20\ mil\ km}^2}{2\ horas}= \frac{{50\ mil\ km}^2}{∆t_{2}}\)
\(\frac{20000}{2\ }= \frac {50000}{∆t_{2}}\)
\(20000∙∆t_{2}=50000∙2\)
\(20000∙∆t_{2}=100000\)
\(∆t_{2}=\frac {100000}{20000}\)
\(∆t_{2}=5\ horas\)
Um satélite se movendo ao redor de Júpiter percorreu uma área de 17 mil km2 em 10 horas. Quanto tempo, em segundos, ele demorará para percorrer uma área de 340 mil km2 ?
a) 340.00 segundos
b) 200.000 segundos
c) 72.000 segundos
d) 200 segundos
e) 720.000 segundos
Letra E
Utilizando a fórmula da segunda lei de Kepler:
\(\frac {A_{1}} {∆t_{1}}=\frac {A_{2}}{∆t_{2}}\)
\(\frac{{17\ mil\ km}^2}{10\ horas}=\frac {{340\ mil\ km}^2}{∆t_{2}}\)
\(\frac{17000}{10}=\frac {340000}{∆t_{2}}\)
\(17000∙∆t_2=340000∙10\)
\(17000∙∆t_2=340000\)
\(∆t_2=\frac{3400000}{17000}\)
\(∆t_2=200 horas\)
Como o valor foi pedido em segundos, faremos a conversão:
\(1\ hora\ —3600 segundos\)
\(200\ horas\ —x \)
\(x=200\bullet3600\)
\(x=720.000\ segundos\)
Um planeta se move ao redor do Sol e descreveu uma área de 5∙1010 m2 em 18 horas. Em 30 horas ele descreverá qual área, em m2 , aproximadamente?
a) \(18,33{\bullet10}^{10\ }m^2\)
b) \(8{\bullet10}^{10\ }m^2\)
c) \(5,33{\bullet10}^{10\ }m^2\)
d) \(8,33{\bullet10}^{10\ }m^2\)
e) \(5{\bullet10}^{10\ }m^2\)
Letra D
Utilizando a fórmula da segunda lei de Kepler:
\(\frac {A_{1}} {∆t_{1}}=\frac {A_{2}}{∆t_{2}}\)
\(\frac{5{\bullet10}^{10}}{18}=\frac{A_2}{30}\)
\(8,33{\bullet10}^{10\ }m^2\approx A_2\)
De acordo com nossos estudos sobre a segunda lei de Kepler, determine de qual outra forma ela pode ser conhecida.
a) Lei dos períodos.
b) Lei das áreas.
c) Lei dos tempos.
d) Lei das constantes.
e) Lei das órbitas.
Letra B
A segunda lei de Kepler é conhecida como lei das áreas. A lei dos períodos se trata da terceira lei de Kepler, e a lei das órbitas se trata da primeira lei de Kepler.
Para o desenvolvimento da segunda lei de Kepler, ele baseou suas observações e comprovações a respeito da órbita excêntrica de qual planeta?
a) Terra
b) Lua
c) Júpiter
d) Marte
e) Netuno
Letra D
Johannes Kepler baseou seus estudos e comprovações observando a órbita do planeta Marte.
