Exercícios sobre tópicos fundamentais de Física
(Unifesp) A oxigenoterapia, tratamento terapêutico com gás oxigênio, é indicada para pacientes que apresentam falta de oxigênio no sangue, tais como portadores de doenças pulmonares. O gás oxigênio usado nesse tratamento pode ser comercializado em cilindros a elevada pressão, nas condições mostradas na figura.
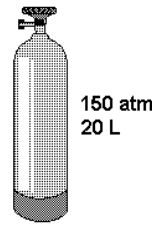
No cilindro, está indicado que o conteúdo corresponde a um volume de 3 m3 de oxigênio nas condições ambientes de pressão e temperatura, que podem ser consideradas como sendo 1 atm e 300 K, respectivamente.
Dado R = 0,082 atm.L.K-1.mol-1, a massa de oxigênio, em kg, armazenada no cilindro de gás representado na figura é, aproximadamente:
DADO: Massa molar do oxigênio = 16 g/mol
a) 0,98.
b) 1,56.
c) 1,95.
d) 2,92.
e) 3,90.
LETRA “E”
Utilizando a equação de Clapeyron (Macete: Por Você Nunca Rezei Tanto), podemos determinar a massa de oxigênio no cilindro:
P.V = N.R.T
150.20 = N . 0,082.300
3000 = N . 24,6
N ≈ 122 mol
Sabendo que a massa molar do oxigênio é de 16 g/mol e que a massa molar resulta da razão da massa pelo número de mol, temos:
M = m ÷ N
m = M . N
m = (2x16) . 122
m = 32 . 122
m = 3904 g = 3,904 kg
Um móvel executa um movimento uniforme com velocidade igual a 72 km/h. Se esse móvel partir da posição 5 m de uma reta numerada, em quanto tempo ele chegará à posição 55 m?
a) 3,0 s
b) 3,5 s
c) 2,0 s
d) 2,5 s
e) 1,5 s
LETRA “D”
Do enunciado da questão, podemos entender:
Velocidade: 72 km/h → 72 ÷ 3,6 = 20 m/s
Posição inicial: S0 = 5m
Posição final: S = 55 m
Aplicando a equação do “SorVeTe”, temos que:
S = S0 + V.t
55 = 5 + 20.t
20.t = 55 – 5
20.t = 50
t = 50 ÷ 20 = 2,5 s
Um garoto puxa um carrinho de madeira que possui massa igual a 500 g. Determine a aceleração em m/s2 dada ao carrinho sabendo que a força aplicada pelo garoto é de 2 N.
a) 4
b) 3
c) 2
d) 5
e) 8
LETRA “A”
Utilizando a segunda lei de Newton (Faça mais amor), temos:
F = m.a
A massa deve ser utilizada em kg, portanto, 500 g = 0,5 kg:
2 = 0,5. a
a = 2 ÷ 0,5
a = 4 m/s2
Qual seria o peso de um astronauta na Lua sabendo que na Terra a sua massa é de 80 kg?
DADOS: Gravidade da Lua: gLUA = 1,6 m/s2;
Gravidade da Terra: gTERRA = 10 m/s2
a) 300 N
b) 280 N
c) 200 N
d) 128 N
e) 228 N
LETRA “D”
Sabendo que a força peso é dada pelo produto da massa pela gravidade (“só se vendem roupas p, m ou g”) e que a massa de um corpo é a mesma em qualquer lugar, podemos escrever que:
PLUA = m . gLUA
PLUA = 80. 1,6
PLUA = 128 N
Considere que um objeto em formato cúbico com 5 cm de aresta seja mergulhado em água de modo que metade de seu volume permaneça submersa. Determine o empuxo sobre esse objeto.
DADO: Gravidade da Terra: gTERRA = 10 m/s2; densidade da água: 103 kg/m3.
a) 0,625 N
b) 0,300 N
c) 0,555 N
d) 0,765 N
e) 0,100 N
LETRA “A”
Determinação do volume do cubo:
V = a3
V = (5 cm)3
V = (5 x 10-2 m)3
V = 125 x 10-6 m3
Aplicando a equação do empuxo (Empuxo é DeVaGar), podemos escrever:
E = d . V . g
E = 103 . 62,5 x 10-6 . 10
Utilizamos apenas metade do volume porque o cubo possui metade de seu volume imersa em água.
E = 62,5 x 10 – 2
E = 0,625 N
Um objeto opaco é colocado sobre o centro de curvatura de um espelho esférico côncavo. Sabendo que o foco do espelho é de 5 cm, determine a posição da formação da imagem e o tipo de imagem formada.
a) 10 cm, virtual
b) 10 cm, real
c) 5 cm, virtual
d) 15 cm, real
e) 20 cm, real
LETRA “B”
Aplicando a equação dos pontos conjugados (Uma Flor é uma Pétala mais uma Petalinha):
1/F = 1/p + 1/p'
Sabendo que o centro de curvatura está em um ponto que corresponde ao dobro do valor do foco, temos:
1/5 = 1/10 + 1/p'
1/p' = 1/5 – 1/10
1/p' = 0,2 – 0,1
1/p' = 0,1
p' = 1 ÷ 0,1 = 10 cm
Com o objeto sobre o centro de curvatura, a imagem é real, igual e invertida.






