Exercícios sobre a velocidade relativa
(IFBA) Dois veículos A e B trafegam em uma rodovia plana e horizontal, obedecendo às seguintes equações horárias cujas unidades estão expressas no Sistema internacional de medidas (S.I.):
XA = 200,0 + 10,0t e XB = 1000,0 – 30,0t
Ao analisar esses movimentos, pode-se afirmar que a velocidade relativa de afastamento dos veículos, em km/h, vale:
a) 20,0
b) 40,0
c) 80,0
d) 100,0
e) 144,0
LETRA E
As equações fornecidas pelo enunciado originaram da equação da função horária da posição no movimento uniforme:
\(S = S_0 + v \cdot t \)
É possível observar que o veículo A tem posição inicial igual a 200 m e velocidade igual a 10 m/s, já o veículo B tem posição inicial igual a 1000 m e velocidade igual a -30 m/s, significando que está se deslocando no sentido oposto ao do veículo A.
Então, calcularemos a velocidade relativa de afastamento em sentido oposto, através da sua fórmula:
\(v_{\text{rel}} = v_1 + v_2 \)
\(v_{\text{rel}} = 10 + 30\)
\(v_{\text{rel}} = 40 \, \text{m/s} \)
Convertendo de m/s para km/h, obtemos:
\(v_{\text{rel}} = 40 \, \text{m/s} \cdot 3.6 = 144 \, \text{km/h} \)
(FEI) Dois móveis A e B, ambos com movimento uniforme, percorrem uma trajetória retilínea conforme mostra a figura. Em t = 0, estes se encontram, respectivamente, nos pontos A e B na trajetória. As velocidades dos móveis são \(v_A = 50 \, \text{m/s} \) e \(v_B = 30 \, \text{m/s} \) no mesmo sentido.
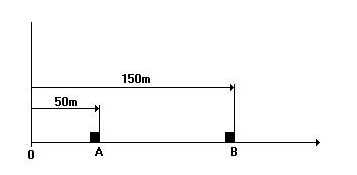
Em qual ponto da trajetória ocorrerá o encontro dos móveis?
a) 200 m
b) 225 m
c) 250 m
d) 300 m
e) 350 m
LETRA D
Primeiramente, desenvolveremos equações para cada móvel empregando a equação da função horária da posição no movimento uniforme:
\(S = S_0 + v \cdot t \)
O móvel A:
\(S_A = 50 + 50 \cdot t \)
O móvel B:
\(S_B = 150 + 30 \cdot t \)
Igualando as equações descobriremos depois de quanto tempo eles irão se encontrar:
\(S_A = S_B \)
\(50 + 50 \cdot t = 150 + 30 \cdot t \)
\(50 \cdot t - 30 \cdot t = 150 - 50 \)
\(20 \cdot t = 100 \)
\(t = \frac{100}{20} \)
\(t = 5s\)
Depois substituiremos o tempo em qualquer uma das equações, assim obteremos o ponto da trajetória em que ocorrerá o encontro dos móveis:
\(S_A = 50 + 50 \cdot t \)
\(S_A = 50 + 50 \cdot 5 \)
\(S_A = 300m\)
(Unitau) Uma motocicleta com velocidade constante de 20 m/s ultrapassa um trem de comprimento 100 m e velocidade 15 m/s. A duração da ultrapassagem é:
a) 5 s
b) 15 s
c) 20 s
d) 25 s
e) 30 s
LETRA C
Primeiramente, calcularemos a velocidade relativa de afastamento no mesmo sentido, através da sua fórmula:
\(v_{\text{rel}} = v_1 - v_2 \)
\(v_{\text{rel}} = 20 - 15 \)
\(v_{\text{rel}} = 5 \, \text{m/s} \)
Por fim, calcularemos a duração da ultrapassagem através da fórmula da velocidade:
\(v = \frac{\Delta S}{\Delta t} \)
\(5 = \frac{100}{\Delta t} \)
\(\Delta t = \frac{100}{5} \)
\(\Delta t = 20s \)
(FEI-SP) Dois automóveis partem no mesmo instante de duas cidades distantes 500 km uma da outra. O automóvel A trafega com velocidade constante de módulo 80 km/h, e o automóvel B trafega com velocidade constante de módulo 120 km/h. Após quanto tempo da partida a distância entre os dois será de 200 km, sabendo que os dois trafegam em sentidos opostos ao longo da mesma estrada retilínea?
a) 0,5 h
b) 1,0 h
c) 1,5 h
d) 2,5 h
e) 3,0 h
LETRA C
Primeiramente, calcularemos a velocidade relativa de aproximação no sentido oposto, através da sua fórmula:
\(v_{\text{rel}} = v_1 + v_2 \)
\(v_{\text{rel}} = 80 + 120 \)
\(v_{\text{rel}} = 200 \, \text{km/h} \)
Por fim, calcularemos o tempo após a partida através da fórmula que o relaciona à velocidade relativa e à variação da distância relativa.
\(v_{\text{rel}} = \frac{\Delta S_{\text{rel}}}{\Delta t} \)
A variação da distância relativa entre os automóveis é 300 km, já que, considerando que o veículo A está parado, o veículo B terá que percorrer 300 km para que a distância entre eles seja de 200 km.
\(v_{\text{rel}} = \frac{\Delta S_{\text{rel}}}{\Delta t} \)
\(200 = \frac{300}{\Delta t} \)
\(\Delta t = \frac{300}{200} \)
\(\Delta t = 1,5 h\)
Calcule a velocidade relativa entre dois corpos à velocidade 60 m/s e 48 m/s que se aproximam no mesmo sentido da trajetória.
a) 12 m/s
b) 15 m/s
c) 18 m/s
d) 21 m/s
e) 23 m/s
LETRA A
Nesse caso temos uma aproximação ocorrendo no mesmo sentido, então calcularemos a velocidade relativa pela fórmula:
\(v_{\text{rel}} = v_1 - v_2 \)
\(v_{\text{rel}} = 60 - 48 \)
\(v_{\text{rel}} = 12m/s \)
Um carro percorre uma avenida a 75 km/h quando alcança outro carro a 85 km/h que está no sentido oposto. De acordo com essas informações, qual é a velocidade relativa entre eles?
a) 150 km/h
b) 160 km/h
c) 170 km/h
d) 180 km/h
e) 190 km/h
LETRA B
Nesse caso temos uma aproximação ocorrendo em sentidos opostos, então calcularemos a velocidade relativa pela fórmula:
\(v_{\text{rel}} = v_1 + v_2 \)
\(v_{\text{rel}} = 75 + 85 \)
\(v_{\text{rel}} = 160 km/h \)
Em um aniversário infantil, duas crianças decidem brincar de apostar corrida. Enquanto uma corre a uma velocidade de 5 km/h, a outra corre a 3 km/h. Calcule a velocidade relativa quando a criança de maior velocidade se afasta da outra.
a) 0,5 km/h
b) 1 km/h
c) 2 km/h
d) 3 km/h
e) 4 km/h
LETRA C
Nesse caso temos um afastamento ocorrendo no mesmo sentido, então calcularemos a velocidade relativa pela fórmula:
\(v_{\text{rel}} = v_1 - v_2 \)
\(v_{\text{rel}} = 5 - 3\)
\(v_{\text{rel}} = 2 km/h\)
Em uma corrida de motos, um motoqueiro se move a 20 m/s enquanto outro se move a 10 m/s. Sabendo que o motoqueiro mais rápido já ultrapassou o motoqueiro mais lento e está se afastando no sentido oposto a ele, encontre a velocidade relativa entre ambos:
a) 0 m/s
b) 10 m/s
c) 20 m/s
d) 30 m/s
e) 40 m/s
LETRA D
Nesse caso temos um afastamento ocorrendo em sentidos opostos, então calcularemos a velocidade relativa pela fórmula:
\(v_{\text{rel}} = v_1 + v_2 \)
\(v_{\text{rel}} = 20 + 10 \)
\(v_{\text{rel}} = 30 m/s \)
Um móvel se move a 43 km/h quando um outro móvel se aproxima com velocidade de 55 km/h. Então, de acordo com essas informações, qual é a velocidade relativa entre eles antes que um móvel ultrapasse o outro?
a) 1 km/h
b) 2 km/h
c) 4 km/h
d) 8 km/h
e) 12 km/h
LETRA E
Nesse caso temos uma aproximação ocorrendo no mesmo sentido, então calcularemos a velocidade relativa pela fórmula:
\(v_{\text{rel}} = v_1 - v_2 \)
\(v_{\text{rel}} = 55 - 43 \)
\(v_{\text{rel}} = 12 km/h \)
Duas crianças nadam em uma piscina com velocidade de 1 km/h e 2 km/h. Sabendo que os seus deslocamentos são em sentidos opostos e que elas estão se aproximando, calcule a velocidade relativa entre elas:
a) 3 km/h
b) 4 km/h
c) 5 km/h
d) 6 km/h
e) 7 km/h
LETRA A
Nesse caso temos uma aproximação ocorrendo em sentidos opostos, então calcularemos a velocidade relativa pela fórmula:
\(v_{\text{rel}} = v_1 + v_2 \)
\(v_{\text{rel}} = 2 + 1 \)
\(v_{\text{rel}} = 3 km/h \)
Um automóvel a 80 km/h se move no mesmo sentido de outro automóvel, a 45 km/h, em uma avenida. Depois de alguns segundos, ele acaba ultrapassando-o. A partir disso, calcule a velocidade relativa entre esses automóveis quando estão se afastando.
a) 30 km/h
b) 35 km/h
c) 40 km/h
d) 45 km/h
e) 50 km/h
LETRA B
Nesse caso temos um afastamento ocorrendo no mesmo sentido, então calcularemos a velocidade relativa pela fórmula:
\(v_{\text{rel}} = v_1 - v_2 \)
\(v_{\text{rel}} = 80 - 45 \)
\(v_{\text{rel}} = 35 km/h \)
Um ônibus a 120 km/h se afasta de um carro a 50 km/h que vai à contramão. Levando isso em consideração, qual é a velocidade relativa entre eles?
a) 130 km/h
b) 140 km/h
c) 150 km/h
d) 160 km/h
e) 170 km/h
LETRA E
Nesse caso temos um afastamento ocorrendo em sentidos opostos, então calcularemos a velocidade relativa pela fórmula:
\(v_{\text{rel}} = v_1 + v_2 \)
\(v_{\text{rel}} = 120 + 50 \)
\(v_{\text{rel}} = 170 km/h\)
