Enem: lista de exercícios sobre equação e função polinomial do 1º grau
Com esta lista de exercícios, você testa seus conhecimentos sobre equação e função polinomial do primeiro grau.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
(UEAAM) Uma pequena empresa que fabrica camisetas verificou que o lucro obtido com a venda de seus produtos obedece à função L(x) = 75x – 3000, sendo L(x) o lucro em reais e x o número de camisetas vendidas, para 40 < x ≤ 120. Para que o lucro da empresa chegue a R$ 4.000,00, o menor número de camisetas a serem vendidas é:
A) 97.
B) 96.
C) 95.
D) 94.
E) 93.
Alternativa D.
Seja L(x) = 4.000, então:
L(x) = 4.000
4000 = 75x – 3000
4000 + 3000 = 75x
7000 = 75x
x = 7000 : 75
x = 93,333…
O número mínimo de camisetas que eles deveriam vender é 94.
-
Questão 2
Uma fábrica de panelas opera com um custo fixo mensal de R$ 9 800,00 e um custo variável por panela de R$ 45,00. Cada panela é vendida por R$ 65,00. Seja x a quantidade que deve ser produzida e vendida mensalmente para que o lucro mensal seja igual a 20% da receita.
A soma dos algarismos de x é:
A) 2
B) 3
C) 4
D) 5
E) 6
Alternativa D.
Sabemos que o lucro L tem que ser a diferença entre a receita (R) e o custo (C).
L (x) = R(x) – C (x)
Sabemos que a receita é igual a:
R(x) = 65x
Como o lucro deve ser 20% da receita, então ele é calculado por:
L (x) = 0,2 · 65x
L(x) = 13x
O custo é dado por:
C(x) = 9 800 + 45x
Logo:
L(x) = R(x) – C(x)
13x = 65x – (9800 + 45x)
13x = 65x – 9800 – 45x
13x – 65x + 45x = – 9800
– 7x = – 9800
x = ( – 9800) : ( – 7)
x = 1400
A soma dos algarismos de x é 1 + 4 + 0 + 0 = 5.
-
Questão 3
(Enem 2019) Uma empresa tem diversos funcionários. Um deles é o gerente, que recebe R$ 1 000,00 por semana. Os outros funcionários são diaristas. Cada um deles trabalha 2 dias por semana, recebendo R$ 80,00 por dia trabalhado.
Chamando de X a quantidade total de funcionários da empresa, a quantia Y, em reais, que esta empresa gasta semanalmente para pagar seus funcionários é expressa por:
A) Y = 80X + 920.
B) Y = 80X + 1 000.
C) Y = 80X + 1 080.
D) Y = 160X + 840.
E) Y = 160X + 1 000.
Alternativa D.
O número de funcionários diaristas é dado por X – 1, pois o gerente não é diarista. Então, o valor gasto pela empresa é dado pela lei de formação:
Y = 160 · (X – 1) + 1000
Y = 160X – 320 + 1000
Y = 160X + 840
-
Questão 4
(Enem 2017) Em um mês, uma loja de eletrônicos começa a obter lucro já na primeira semana. O gráfico representa o lucro (L) dessa loja desde o início do mês até o dia 20. Mas esse comportamento se estende até o último dia, o dia 30.
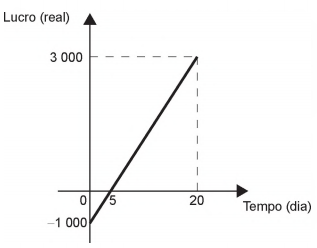
A representação algébrica do lucro (L) em função do tempo (t) é:
A) L(t) = 20t + 3 000
B) L(t) = 20t + 4 000
C) L(t) = 200t
D) L(t) = 200t – 1 000
E) L(t) = 200t + 3 000
Alternativa D.
Analisando o gráfico, é possível perceber que ele é uma função do 1º grau, da forma L(t) = at + b.
Note que o gráfico parte do ponto (0, – 1000), ou seja, quando t = 0 L(t) = – 1000, então b = – 1000.
Logo, a função será:
L(t) = at – 1000
Agora, para encontrar o valor de a, basta analisar que, quando t = 20, L(t) = 3000.
Substituindo na fórmula, teremos:
3000 = 20a – 1000
3000 + 1000 = 20a
4000 = 20a
a = 4000/20
a = 200
Então, a representação algébrica será:
L(t) = 200t – 1000
-
Questão 5
(Enem 2018) Uma indústria automobilística está testando um novo modelo de carro. Cinquenta litros de combustível são colocados no tanque desse carro, que é dirigido em uma pista de testes até que todo o combustível tenha sido consumido. O segmento de reta no gráfico mostra o resultado desse teste, no qual a quantidade de combustível no tanque é indicada no eixo y (vertical), e a distância percorrida pelo automóvel é indicada no eixo x (horizontal).
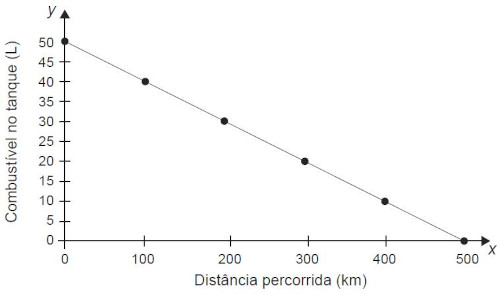
A expressão algébrica que relaciona a quantidade de combustível no taque e a distância percorrida pelo automóvel é:
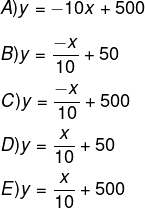
Alternativa B.
Note que o gráfico é uma reta, o que faz com que essa expressão algébrica seja de uma função polinomial do 1º grau.
y = ax + b
Analisando o gráfico, sabemos que, quando x = 0, y = 50.
50 = a · 0 + b
50 = b
Logo, podemos representar a expressão algébrica por:
y = ax + 50
Podemos observar também que, quando y = 0, x = 500, então:
0 = 500a + 50
– 50 = 500a
a = - 50
500a = - 1
10A expressão algébrica procurada é:
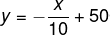
-
Questão 6
(Enem 2017) Um sítio foi adquirido por R$ 200 000,00. O proprietário verificou que a valorização do imóvel, após sua aquisição, cresceu em função do tempo conforme o gráfico, e que essa tendência de valorização se manteve nos anos seguintes.
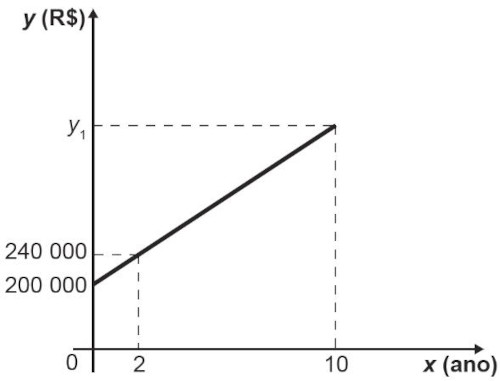
O valor desse sítio, no décimo ano após sua compra, em real, será de:
A) 190 000.
B) 232 000.
C) 272 000.
D) 400 000.
E) 500 000.
Alternativa D.
Sabemos que essa função é polinomial do 1º grau, pois o seu gráfico é uma reta, logo sua lei de formação é f(x) = ax + b. Quando x = 0, y = 200. 000, então b = 200 000. A expressão será f(x) = ax + 200 000.
Para encontrar o valor de a, sabemos que, quando x = 2, y = 240 000, então:
f( 2) = 2a + 200 000
240 000 = 2a + 200 000
240 000 – 200 000 = 2a
40 000 = 2a
40 000 : 2 = a
a = 20 000
A lei de formação da função é f(x) = 20 000x + 200 000. Calcularemos f(10):
f(10) = 20 000 · 10 + 200 000
f(10) = 200 000 + 200 000
f(10) = 400 000
-
Questão 7
(Enem 2016) Um dos grandes desafios do Brasil é o gerenciamento dos seus recursos naturais, sobretudo os recursos hídricos. Existe uma demanda crescente por água e o risco de racionamento não pode ser descartado. O nível de água de um reservatório foi monitorado por um período, sendo o resultado mostrado no gráfico. Suponha que essa tendência linear observada no monitoramento se prolongue pelos próximos meses.
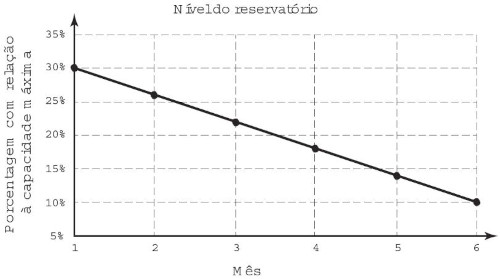
Nas condições dadas, qual o tempo mínimo, após o sexto mês, para que o reservatório atinja o nível zero de sua capacidade?
a) 2 meses e meio.
b) 3 meses e meio.
c) 1 mês e meio.
d) 4 meses.
e) 1 mês.
Alternativa A.
Analisando o gráfico, ele estava em 30% e foi para 10%, logo houve uma variação de 20% no período de 5 meses. Como em 5 meses houve uma redução de 20%, então, para que o volume atinja o marco 0, é necessário que se reduza 10%, que é metade desse tempo, logo são necessários 2 meses e meio.
-
Questão 8
(Cesgranrio) O valor de um carro novo é de R$ 9 000,00 e, com 4 anos de uso, é de R$ 4 000,00. Supondo que o preço caia com o tempo, segundo uma linha reta, o valor de um carro com 1 ano de uso é:
A) R$ 8 250,00.
B) R$ 8 000,00.
C) R$ 7 750,00.
D) R$ 7 500,00.
E) R$ 7 000,00.
Alternativa C.
Sabemos que o valor do veículo desvaloriza de forma linear, logo ele pode ser descrito por uma função polinomial do 1º grau: f(x) = ax + b. Quando x = 0, y = 9 000, então b = 9 000.
Quando x = 4, y = 4 000, logo:
y = ax + b
4 000 = 4a + 9 000
4 000 – 9 000 = 4a
– 5 000 = 4a
4a = – 5 000
a = – 5 000 : 4
a = 1 750
A função é f(x) = – 1 750x + 9 000.
Agora calcularemos o valor de f(1):
f(1) = – 1 750 · 1 + 9 000
f(1) = – 1750 + 9 000
f(1) = 7 250
-
Questão 9
(Enem 2009) Um grupo de 50 pessoas fez um orçamento inicial para organizar uma festa, que seria dividido entre elas em cotas iguais. Verificou-se ao final que, para arcar com todas as despesas, faltavam R$ 510,00, e que 5 novas pessoas haviam ingressado no grupo. No acerto foi decidido que a despesa total seria dividida em partes iguais pelas 55 pessoas. Quem não havia ainda contribuído pagaria a sua parte, e cada uma das 50 pessoas do grupo inicial deveria contribuir com mais R$ 7,00.
De acordo com essas informações, qual foi o valor da cota calculada no acerto final para cada uma das 55 pessoas?
A) R$ 14,00.
B) R$ 17,00.
C) R$ 22,00.
D) R$ 32,00.
E) R$ 57,00.
Alternativa D.
Seja x o valor pago por cada pessoa. A despesa pode ser representada por D = 55x. Inicialmente 50 pessoas pagariam x – 7 e faltavam 510 reais para pagar a despesa, ou seja:
D = 50 ( x – 7 ) + 510
Igualando as duas equações, temos que:
55x = 50 (x – 7) + 510
55x = 50x – 350 + 510
55x – 50x = 160
5x = 160
x = 160 : 5
x = 32
Logo, cada um pagará 32 reais.
-
Questão 10
(Enem) O saldo de contratações no mercado formal no setor varejista da região metropolitana de São Paulo registrou alta. Comparando as contratações deste setor no mês de fevereiro com as de janeiro deste ano, houve incremento de 4 300 vagas no setor, totalizando 880 605 trabalhadores com carteira assinada.
Disponível em: http://www.folha.uol.com.br. Acesso em: 26 abr. 2010 (adaptado).
Suponha que o incremento de trabalhadores no setor varejista seja sempre o mesmo nos seis primeiros meses do ano.
Considerando-se que y e x representam, respectivamente, as quantidades de trabalhadores no setor varejista e os meses, janeiro sendo o primeiro, fevereiro, o segundo, e assim por diante, a expressão algébrica que relaciona essas quantidades nesses meses é:
A) y = 4 300x
B) y = 884 905x
C) y = 872 005 + 4 300x
D) y = 876 305 + 4 300x
E) y = 880 605 + 4 300x
Alternativa C.
Sabemos que, em janeiro, houve um incremento de 4 300, totalizando 880 605. Logo, antes de janeiro, havia um total de 880 605 – 4 300 = 87 2005 trabalhadores. Sabemos que, para cada mês x, há um incremento de 4 300 funcionários, logo podemos descrever como 4 300x. Então, a expressão algébrica será:
y = 872 005 + 4 300x
-
Questão 11
(Cefet - MG - 2015) Um motorista de táxi cobra, para cada corrida, uma taxa fixa de R$ 5,00 e mais R$ 2,00 por quilômetro rodado. O valor total arrecadado (R) num dia é função da quantidade total (x) de quilômetros percorridos e calculado por meio da função R(x) = ax + b, em que a é o preço cobrado por quilômetro e b, a soma de todas as taxas fixas recebidas no dia. Se, em um dia, o taxista realizou 10 corridas e arrecadou R$ 410,00, então a média de quilômetros rodados por corrida foi de:
A) 14
B) 16
C) 18
D) 20
Alternativa C.
Sabemos que R(x) = ax + b. Note que a taxa fixa é de 5,00 → b = 5.
É cobrado o total de 2,00 por km rodado, logo a = 2. A função que descreve essa situação é:
R(x) = 2x + 5
Ele arrecadou um total de 410 reais, então encontraremos o valor de x para R(x) = 410.
410 = 10(2x + 5)
410 : 10 = 2x + 5
41 = 2x + 5
41 – 5 = 2x
36 =2x
36 : 2 = x
x = 18
-
Questão 12
(UCS 2014) O salário mensal de um vendedor é de R$ 750,00 fixos mais 2,5% sobre o valor total em reais das vendas que ele efetuar durante o mês. Em um mês em que suas vendas totalizarem x reais, o salário do vendedor será dado pela expressão:
A) y = 750 + 2,5x
B) y = 750 + 0,25x
C) y = 750,25x
D) y= 750 . (0,25x)
E) 750 + 0,025x
Alternativa E.
O salário mensal é uma função do 1º grau, logo pode ser descrito por y = ax+b. Ele tem um fixo de 750 reais, então b = 750. Além disso, ele recebe 2,5% do valor x arrecadado, ou seja, 0,025x %.
A expressão procurada é: y = 750 + 0,025.
-
Questão 13
(Enem 2012) A tabela seguinte apresenta a média, em kg, de resíduos domiciliares produzidos anualmente por habitante, no período de 1995 a 2005.
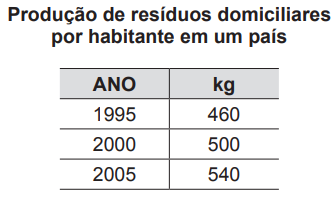
Se essa produção continuar aumentando, mantendo o mesmo padrão observado na tabela, a previsão de produção de resíduos domiciliares, por habitante no ano de 2020, em kg, será:
A) 610.
B) 640.
C) 660.
D) 700.
E) 710.
Alternativa C.
Note que há uma relação entre o tempo e a produção de resíduos, pois, de 5 em 5 anos, há um aumento de 40 kg. De 2005 até 2020, há 15 anos, que correspondem a 3 ciclos, logo haverá um aumento de 3 · 40 = 120 kg. Agora basta somar 120 + 540 = 660 kg.
-
Questão 14
(Enem 2011) O prefeito de uma cidade deseja construir uma rodovia para dar acesso a outro município. Para isso, foi aberta uma licitação na qual concorreram duas empresas. A primeira cobrou R$ 100 000,00 por km construído (n), acrescidos de um valor fixo de R$ 350 000,00, enquanto a segunda cobrou R$ 120 000,00 por km construído (n) acrescido de um valor fixo de R$ 150 000,00. As duas empresas apresentam o mesmo padrão de qualidade dos serviços prestados, mas apenas uma delas poderá ser contratada.
Do ponto de vista econômico, qual equação possibilitaria encontrar a extensão da rodovia que tornaria indiferente para a prefeitura escolher qualquer uma das propostas apresentadas?
A) 100n + 350 = 120n + 150
B) 100n + 150 = 120n + 350
C) 100(n + 350) = 120(n + 150)
D) 100(n + 350 000) = 120(n + 150 000)
E) 350(n + 100 000) = 150(n + 120 000)
Alternativa A.
Podemos descrever essa situação pela equação:
A equação que representa o valor da primeira empresa é V1= 100 000n + 350 000, e a da segunda empresa é V2 = 120 000n + 150 000.
Igualando as duas equações, temos que:
100 000n + 350 000 = 120 000n + 150 000
Dividindo por 1000, a equação será:
100n + 350 = 120n + 150
-
Questão 15
(Enem 2016) Uma cisterna de 6 000 L foi esvaziada em um período de 3h. Na primeira hora foi utilizada apenas uma bomba, mas nas duas horas seguintes, a fim de reduzir o tempo de esvaziamento, outra bomba foi ligada junto com a primeira. O gráfico, formado por dois segmentos de reta, mostra o volume de água presente na cisterna, em função do tempo.
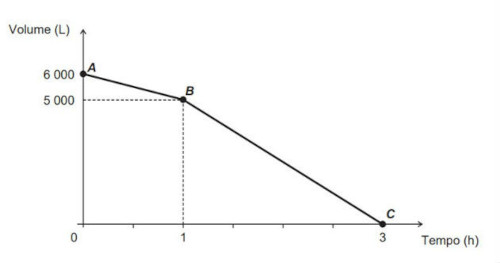
Qual é a vazão, em litro por hora, da bomba que foi ligada no início da segunda hora?
A) 1 000
B) 1 250
C) 1 500
D) 2 000
E) 2 500
Alternativa C.
Primeiro encontraremos a vazão da primeira bomba. Analisando o gráfico, no primeiro caso, houve uma vazão de 1000 L em uma hora, logo a vazão é de 1000L/h.
Quando a segunda bomba é ligada, podemos observar que, em 2 horas, foram retirados 5000L do reservatório, então a vazão foi de 5000 : 2 = 2500 L/ h. Retirando a vazão da bomba anterior, temos que: 2500 – 1000 = 1500 L/h.
-
Questão 16
(Vunesp 2018) Em uma caixa há parafusos e pregos, num total de 20 unidades. Sabendo que há 4 parafusos a mais do que o número de pregos, então o número de parafusos dessa caixa é:
A) 12.
B) 4.
C) 8.
D) 10.
E) 6.
Alternativa A.
Seja x o número de pregos, então o número de parafusos é igual a x + 4. Sabemos que:
x + x + 4 = 20
2x + 4 = 20
2x = 20 – 4
2x = 16
x = 16 : 2
x = 8
Se há 8 pregos, então 8 + 4 = 12 parafusos.
-
Questão 17
(Enem 2012) As curvas de oferta e de demanda de um produto representam, respectivamente, as quantidades que vendedores e consumidores estão dispostos a comercializar em função do preço do produto. Em alguns casos, essas curvas podem ser representadas por retas. Suponha que as quantidades de oferta e de demanda de um produto sejam, respectivamente, representadas pelas equações:
QO = –20 + 4P
QD = 46 – 2P
em que QO é quantidade de oferta, QD é a quantidade de demanda e P é o preço do produto.
A partir dessas equações, de oferta e de demanda, os economistas encontram o preço de equilíbrio de mercado, ou seja, quando QO e QD se igualam.
Para a situação descrita, qual o valor do preço de equilíbrio?
A) 5
B) 11
C) 13
D) 23
E) 33
Alternativa B.
Para encontrar o preço de equilíbrio, vamos igualar as equações:
– 20 + 4P = 46 – 2P
4P + 2P = 46 + 20
6P = 66
P = 66 : 6
P = 11
-
Questão 18
(Enem 2010) Em fevereiro, o governo da Cidade do México, metrópole com uma das maiores frotas de automóveis do mundo, passou a oferecer à população bicicletas como opção de transporte. Por uma anuidade de 24 dólares, os usuários têm direito a 30 minutos de uso livre por dia. O ciclista pode retirar em uma estação e devolver em qualquer outra e, se quiser estender a pedalada, paga 3 dólares por hora extra.
Revista Exame. 21 abr. 2010.
A expressão que relaciona o valor f pago pela utilização da bicicleta por um ano, quando se utilizam x horas extras nesse período é:
A) f(x) = 3x
B) f(x) = 24
C) f(x) = 27
D) f(x) = 3x + 24
E) f(x) = 24x + 3
Alternativa D.
Sabemos que o valor pago é composto por uma taxa fixa de 24 reais mais uma taxa variável de 3 reais a cada hora extra, ou seja, de 3x, então a expressão será: f(x) = 3x + 24.
-
Questão 19
(Enem) Por muitos anos, o Brasil tem figurado no cenário mundial entre os maiores produtores e exportadores de soja. Entre os anos de 2010 e 2014, houve uma forte tendência de aumento da produtividade, porém, um aspecto dificultou esse avanço: o alto custo do imposto ao produtor associado ao baixo preço de venda do produto. Em média, um produtor gastava R$ 1 200,00 por hectare plantado, e vendia por R$ 50,00 cada saca de 60 kg. Ciente desses valores, um produtor pode, em certo ano, determinar uma relação do lucro L que obteve em função das sacas de 60 kg vendidas. Suponha que ele plantou 10 hectares de soja em sua propriedade, na qual colheu x sacas de 60 kg e todas as sacas foram vendidas.
Disponível em: www.cnpso.embrapa.br. Acesso em: 27 fev. 2012 (adaptado).
Qual é a expressão que determinou o lucro L em função de x obtido por esse produtor nesse ano?
A) L(x) = 50x – 1 200
B) L(x) = 50x – 12 000
C) L(x) = 50x + 12 000
D) L(x) = 500x – 1 200
E) L(x) = 1 200x – 500
Alternativa B.
O lucro é a diferença entre o ganho e o valor gasto. Como há 10 hectares e o gasto é de 1200 por hectare, então o valor gasto será de 10 · 1200 = 12000.
A receita é de 50 reais a cada saca de 60 kg, ou seja, 50x, então o lucro pode ser calculado por:
L(x) = 50x – 12 000
-
Questão 20
(Enem 2011) Uma professora realizou uma atividade com seus alunos utilizando canudos de refrigerante para montar figuras, onde cada lado foi representado por um canudo. A quantidade de canudos (C) de
cada figura depende da quantidade de quadrados (Q) que formam cada figura. A estrutura de formação das figuras está representada a seguir.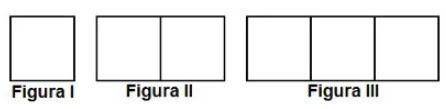
Que expressão fornece a quantidade de quadrados de cada figura?
A) C = 4Q
B) C = 3Q + 1
C) C = 4Q + 1
D) C = Q + 3
E) C = 4Q – 2
Alternativa B.
Analisando as imagens, temos que:
Figura 1
4 canudos → 1 quadrado
Figura 2
7 canudos → 2 quadrados
Figura 3
10 canudos → 3 quadrados
Podemos observar que o primeiro quadrado é composto por 4 canudos, mas, para fazer os demais, a cada quadrado a mais, acrescentamos 3 palitos. Então, a lei de formação que descreve essa situação é C = 3Q + 1.