Enem: lista de exercícios sobre escala, densidade e velocidade média
Com esta lista de exercícios, você pode testar seus conhecimentos sobre o cálculo das razões estabelecidas na escala, densidade e velocidade média.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
(Uncisal 2019) A régua, o barbante e o mapa mostrados a seguir foram utilizados por um estudante para fazer o seguinte procedimento a fim de calcular o comprimento do Rio Amazonas:
1. cobriu com o barbante a linha do mapa que representa o Rio Amazonas, desde a nascente até a foz;
2. esticou o barbante;
3. mediu com a régua o comprimento do barbante e obteve 14,8 cm;
4. verificou que o mapa foi construído na escala 17: 800 000 000.
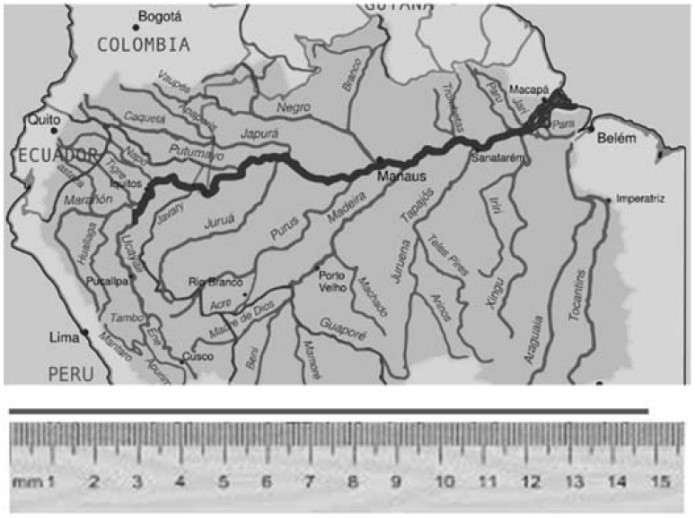
Disponível em: https://upload.wikimedia.org.
Acesso em: 23 nov. 2018 (adaptado).Considerando-se a escala utilizada na construção do mapa e o comprimento do barbante, qual é o valor que mais se aproxima do comprimento do Rio Amazonas?
A) 31 000 km.
B) 25 100 km.
C) 11 800 km.
D) 7 000 km.
E) 2 000 km.
Alternativa D.
Sabemos que 800 000 000 cm equivalem a 8 000 km.
Montando as razões, temos que17 está para 8 000, assim como 14,8 está para x:
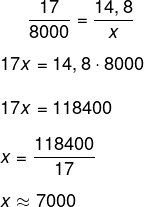
-
Questão 2
2018 PPL) Um vaso decorativo quebrou e os donos vão encomendar outro para ser pintado com as mesmas características. Eles enviam uma foto do vaso na escala 1 : 5 (em relação ao objeto original) para um artista. Para ver melhor os detalhes do vaso, o artista solicita uma cópia impressa da foto com dimensões triplicadas em relação às dimensões da foto original. Na cópia impressa, o vaso quebrado tem uma altura de 30 centímetros.
Qual é a altura real, em centímetros, do vaso quebrado?
A) 2.
B) 18.
C) 50.
D) 60.
E) 90.
Alternativa C.
Sabemos que a altura de 30 cm equivale a 3 vezes a altura do vaso, então 30 : 3 = 10 cm no tamanho do desenho. Sabendo que cada centímetro do desenho equivale a 5 cm no tamanho real, então: 10 · 5 = 50 cm.
-
Questão 3
2016) Num mapa com escala 1 : 250 000, a distância entre as cidades A e B é de 13 cm. Num outro mapa, com escala 1 : 300 000, a distância entre as cidades A e C é de 10 cm. Em um terceiro mapa, com escala 1 : 500 000, a distância entre as cidades A e D é de 9 cm. As distâncias reais entre a cidade A e as cidades B, C e D são, respectivamente, iguais a X, Y e Z (na mesma unidade de comprimento). As distâncias X, Y e Z, em ordem crescente, estão dadas em:
A) X , Y , Z.
B) Y , X , Z.
C) Y , Z , X.
D) Z , X , Y.
E) Z , Y , X.
Alternativa B.
Para comparar as distâncias, vamos primeiro encontrar a distância real entre as cidades.
- Distância entre A e B:
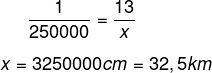
- Distância entre A e C:
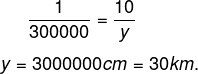
- Distância entre A e D:
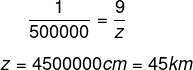
Então, temos que Y < X < Z.
-
Questão 4
(IFSP) Uma peça de ferro foi colocada em um becker graduado que continha 200 mL de água (figura 1). A peça ficou completamente submersa e a água não transbordou, atingindo o nível da água conforme a figura 2.
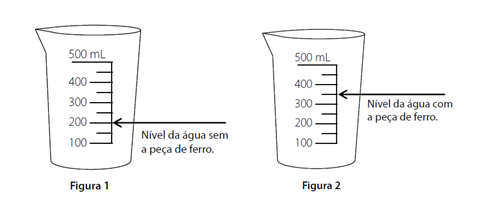
Sabendo que a peça de ferro tem massa de 1,125 kg, é possível determinar que a densidade do material dessa peça é, em g/cm3:
A) 0,0075.
B) 0,075.
C) 0,75.
D) 7,5
E) 75
Alternativa D.
Sabemos que 1,125 kg correspondem a 1125 gramas. Como houve um aumento de 150 mL, sabendo que 1 mL corresponde a 1 cm³, para encontrar a densidade, basta dividir 1125 por 150 mL:
1125 : 150 = 7,5
-
Questão 5
(Enem 2016) Densidade absoluta (d) é a razão entre a massa de um corpo e o volume por ele ocupado. Um professor propôs à sua turma que os alunos analisassem a densidade de três corpos: dA, dB, dC. Os alunos verificaram que o corpo A possuía 1,5 vez a massa do corpo B e esse, por sua vez, tinha 3/4 da massa do corpo C. Observaram, ainda, que o volume do corpo A era o mesmo do corpo B e 20% maior do que o volume do corpo C.
Após a análise, os alunos ordenaram corretamente as densidades desses corpos da seguinte maneira:
A) dB < dA < dC
B) dB = dA < dC
C) dC < dB = dA
D) dB < dC < dA
E) dC < dB < dA
Alternativa A.
Comparando as massas, colocaremos todas em função da massa de B:
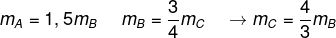
Comparando os volumes, colocaremos todos em função do volume de C:
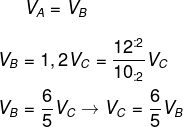
Então, temos que:
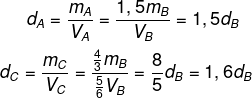
Logo, temos que:
dB < dA < dC
-
Questão 6
(Etec adaptado) O agulhão-bandeira é um recordista em velocidade, podendo chegar a surpreendentes 110 km/h devido a sua forma hidrodinâmica e força física.

Lembre-se de que velocidade escalar média é a razão entre distância percorrida e tempo necessário para se percorrer tal distância. Considerando essa velocidade escalar média constante durante 3 minutos, a distância que esse peixe é capaz de se deslocar é, em metros, de:
A) 180.
B) 330.
C) 1 800.
D) 2 000.
E) 5 500.
Alternativa E.
Vamos transformar a velocidade de km/h para m/s dividindo 110 por 3,6:
110 : 3,6 = 30,555
Sabendo que 3 minutos possuem 180 segundos, então 30,555… · 180 = 5500.
-
Questão 7
(IFMT) Antônio e Marcos partem do ponto O, no mesmo instante, cada um em seu automóvel. Antônio segue pela estrada x à velocidade de 60 Km/h, enquanto Marcos vai pela estrada y à velocidade de 80Km/h.
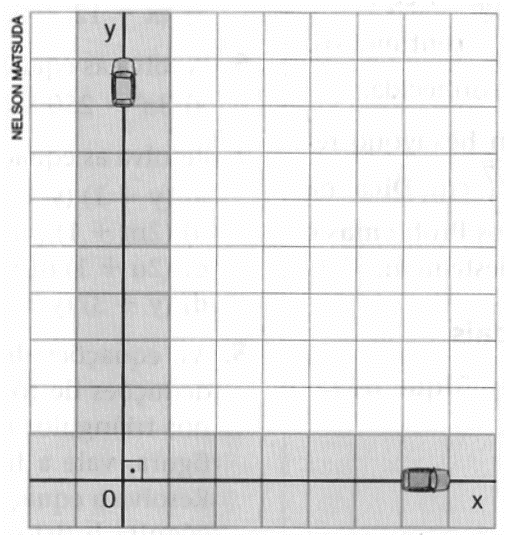
Depois de duas horas, a distância em linha reta percorrida entre eles é igual a:
A) 1000 km.
B) 800 km.
C) 100 km.
D) 200 km.
E) 500 km.
Alternativa D.
Após 2 horas, Antônio terá percorrido 120 km, e Marcos, 160 km. Para encontrar a distância entre eles, basta aplicar o teorema de Pitágoras.
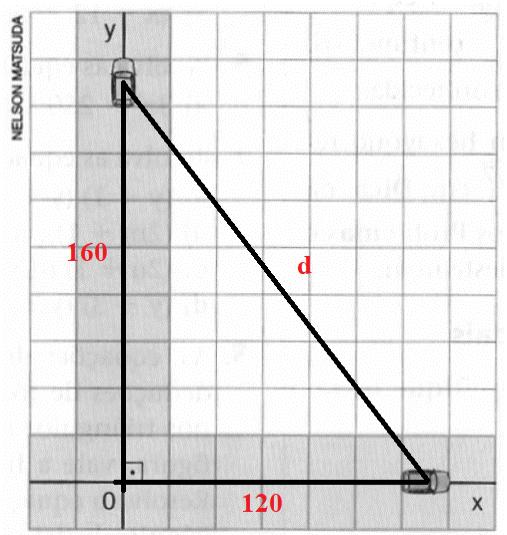
d² = 160² + 120²
d² = 25600 + 14400
d² = 400000
d = √400000
d = 200 m
-
Questão 8
(Enem 2018) Numa atividade de treinamento realizada no Exército de um determinado país, três equipes – Alpha, Beta e Gama – foram designadas a percorrer diferentes caminhos, todos com os mesmos pontos de partida e de chegada.
-
A equipe Alpha realizou seu percurso em 90 minutos com uma velocidade média de 6,0 km/h.
-
A equipe Beta também percorreu sua trajetória em 90 minutos, mas sua velocidade média foi de 5,0 km/h.
-
Com uma velocidade média de 6,5 km/h, a equipe Gama concluiu seu caminho em 60 minutos.
Com base nesses dados, foram comparadas as distâncias dBeta; dAlpha e dGama percorridas pelas três equipes.
A ordem das distâncias percorridas pelas equipes Alpha, Beta e Gama é:
A) dGama < dBeta < dAlpha
B) dAlpha = dBeta < dGama
C) dGama < dBeta = dAlpha
D) dBeta < dAlpha < dGama
E) dGama < dAlpha < dBeta
Calcularemos a distância percorrida por equipe.
Sabemos que 90 minutos correspondem a 1,5 horas e que 60 minutos correspondem a 1 hora, então:
dAlfa= 6 · 1,5 = 9 km
dBeta = 5 · 1,5 = 7,5 km
dGama = 6,5 ·1 = 6,5 km
dGama < dBeta < dAlfa
-
-
Questão 9
(Enem 2010) No monte de Cerro Armazones, no deserto de Atacama, no Chile, ficará o maior telescópio da superfície terrestre, o Telescópio Europeu Extremamente Grande (E-ELT) O E-ELT terá um espelho primário de 42 m de diâmetros, “maior olho do mundo voltado para o céu”.
Disponível em: http://www.estadao.com.br. Acesso em: 27 abr. 2010 (adaptado).
Ao ler esse texto em uma sala de aula, uma professora fez uma suposição de que o diâmetro do olho humano mede aproximadamente 2,1 cm.
Qual a razão entre o diâmetro aproximado do olho humano, suposto pela professora, e o diâmetro do espelho primário do telescópio citado?
A) 1 : 20
B) 1 : 100
C) 1 : 200
D) 1 : 1 000
E) 1 : 2 000
Alternativa E.
Sabemos que 42 metros equivalem a 4200 cm, então:
2,1 : 4200
Dividindo por 2,1 dos dois lados, temos que a escala será de:
1 : 2000
-
Questão 10
(Enem 2011) Sabe-se que a distância real, em linha reta, de uma cidade A, localizada no estado de São Paulo, a uma cidade B, localizada no estado de Alagoas, é igual a 2 000 km. Um estudante, ao analisar um mapa, verificou com sua régua que a distância entre essas duas cidades, A e B, era 8 cm.
Os dados nos indicam que o mapa observado pelo estudante está na escala de:
A) 1 : 250.
B) 1 : 2 500.
C )1 : 25 000.
D) 1 : 250 000.
E) 1 : 25 000 000.
Alternativa E.
Primeiro é necessário transformar 2 000 km para cm. Para isso, basta multiplicar por 100 000.
2 000 · 10 000 = 200 000 000
8 : 200 000 000
Dividindo por 8, temos que:
1 : 25 000 000
-
Questão 11
(Enem 2011) Cerca de 20 milhões de brasileiros vivem na região coberta pela Caatinga, em quase 800 mil km2 de área. Quando não chove, o homem do sertão e sua família precisam caminhar quilômetros em busca da água dos açudes. A irregularidade climática é um dos fatores que mais interferem na vida do sertanejo.
Disponível em: http://www.wwf.org.br. Acesso em: 23 abr. 2010.
Segundo esse levantamento, a densidade demográfica da região coberta pela caatinga, em habitantes por km², é de:
A) 250.
B) 25.
C) 2,5.
D) 0,25.
E) 0,025.
Alternativa B.
Para encontrar a densidade demográfica, vamos dividir 20.000.000 por 800.000:
20.000.000 : 800.000 = 25
-
Questão 12
(Enem 2012) Um biólogo mediu a altura de cinco árvores distintas e representou-as em uma mesma malha quadriculada, utilizando escalas diferentes, conforme indicações na figura a seguir.
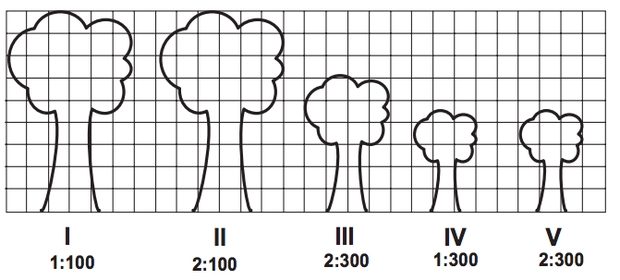
Qual é a árvore que apresenta a maior altura real?
A) I
B) II
C) III
D) IV
E) V
Alternativa D.
Seja c o comprimento de cada quadrado, temos que:
I → 9c: como a escala é 1:100, então o tamanho real é 900c;
II → 9c: como a escala 2:100, então o tamanho real é 450c;
III → 6c: como a escala 2:300, então o tamanho real é 900c;
IV → 4,5c: como a escala 1:300, então o tamanho real é 1350c;
V → 4,5c: como a escala 2:300, então o tamanho real é 675 c.
Logo, a árvore que possui maior altura é a IV.
-
Questão 13
(Enem 2013) A figura apresenta dois mapas, em que o estado do Rio de Janeiro é visto em diferentes escalas.
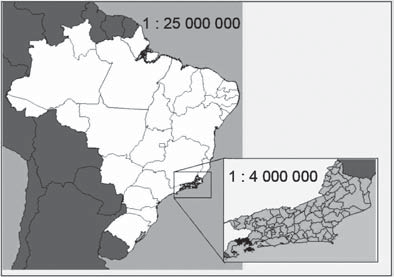
Há interesse em estimar o número de vezes que foi ampliada a área correspondente a esse estado no mapa do Brasil.
Esse número é:
A) menor que 10.
B) maior que 10 e menor que 20.
C) maior que 20 e menor que 30.
D) maior que 30 e menor que 40.
E) maior que 40.
Alternativa D.
Para encontrar o número de vezes que a área foi ampliada, basta calcular o quadrado da divisão entre 25 000 000 e 4 000 000.
(25 000 000 : 4 000 000) ² = 6,25² = 39,06.
Sabemos que esse valor é maior que 30 e menor que 40.
-
Questão 14
(Enem 2012) O esporte de alta competição da atualidade produziu uma questão ainda sem resposta: Qual é o limite do corpo humano? O maratonista original, o grego da lenda, morreu de fadiga por ter corrido 42 quilômetros. O americano Dean Karnazes, cruzando sozinho as planícies da Califórnia, conseguiu correr dez vezes mais em 75 horas.
Um professor de Educação Física, ao discutir com a turma o texto sobre a capacidade do maratonista americano, desenhou na lousa uma pista reta de 60 centímetros, que representaria o percurso referido.
Disponível em: http://veja.abril.com.br. Acesso em: 25 jun. 2011 (adaptado).
Se o percurso de Dean Karnazes fosse também em uma pista reta, qual seria a escala entre a pista feita pelo professor e a percorrida pelo atleta?
A) 1:700
B) 1:7 000
C) 1:70 000
D) 1:700 000
E) 1:7 000 000
Alternativa D.
O atleta percorreu uma distância 10 vezes maior que 42 km, então ele percorreu 420 km. Sabendo que 420 km = 42 000 000 cm, então 60 : 42 000 000 = 1 : 700 000.
-
Questão 15
(Enem 2018) Uma empresa de comunicação tem a tarefa de elaborar um material publicitário de um estaleiro para divulgar um novo navio, equipado com um guindaste de 15 m de altura e uma esteira de 90 m de comprimento. No desenho desse navio, a representação do guindaste deve ter sua altura entre 0,5 cm e 1 cm, enquanto a esteira deve apresentar comprimento superior a 4 cm. Todo o desenho deverá ser feito em uma escala 1 : X.
Os valores possíveis para X são, apenas,
A) X > 1 500.
B) X < 3 000.
C) 1 500 < X < 2 250.
D) 1 500 < X < 3 000.
Alternativa C.
Montando as razões, temos que:
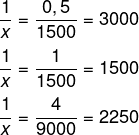
Note que 1500 < x < 2250.
-
Questão 16
(Fuvest) Ao cobrar uma falta em um jogo de futebol, um jogador imprime à bola uma velocidade de 43,2 km/h. Sabendo que a bola gasta 3 s até atingir as redes, determine a distância percorrida.
A) 36 m
B) 48 m
C) 52 m
D) 75 m
E) 28 m
Alternativa A.
A velocidade média é a razão entre o espaço e o tempo. Vamos converter o valor de 43,2 km dividindo por 3,6.
43,2 : 3,6 = 12 metros/segundo
Como ele leva 3 segundos, temos que:
12 · 3 = 36 metros
-
Questão 17
(Enem 2020 Digital) Uma associação desportiva contratou uma empresa especializada para construir um campo de futebol, em formato retangular, com 250 metros de perímetro. Foi elaborada uma planta para esse campo na escala 1 : 2 000. Na planta, a medida do perímetro do campo de futebol, em metro, é:
A) 0,0005
B) 0,125
C) 8
D) 250
E) 500 000.
Alternativa C.
Sabemos que o perímetro é de 250 metros. Para encontrar o valor do perímetro da planta, basta dividir 2 000 por 250 = 8.
-
Questão 18
(Enem 2016) Em uma empresa de móveis, um cliente encomenda um guarda-roupa nas dimensões 220 cm de altura, 120 cm de largura e 50 cm de profundidade. Alguns dias depois o projetista, com o desenho elaborado na escala 1:8, entra em contato com o cliente para fazer sua apresentação. No momento da impressão, o profissional percebe que o desenho não caberia na folha de papel que costumava usar. Para resolver o problema, configurou a impressora para que a figura fosse reduzida em 20%.
A altura, a largura e a profundidade do desenho impresso para a apresentação serão, respectivamente:
A) 22,00 cm, 12,00 cm e 5,00 cm.
B) 27,50 cm, 15,00 cm e 6,25 cm.
C) 34,37 cm, 18,75 cm e 7,81 cm.
D) 35,20 cm, 19,20 cm e 8,00 cm.
E) 44,00 cm, 24,00 cm e 10,00 cm.
Alternativa A.
Sabemos que os lados estão 8 vezes menores, pois a escala é 1 : 8, temos que:
220 : 8 = 27, 5
120 : 8 = 15
50 : 8 = 6,25
Além disso, eles passaram por uma redução de 20%, logo restará 80% de cada dimensão:
27,5 · 0,8 = 22 cm
15 · 0,8 = 12 cm
6,25 · 0,8 = 5 cm
Então, as dimensões são 22 cm, 12 cm e 5 cm.
-
Questão 19
(Enem 2014) A Figura 1 representa uma gravura retangular com 8 m de comprimento e 6 m de altura.
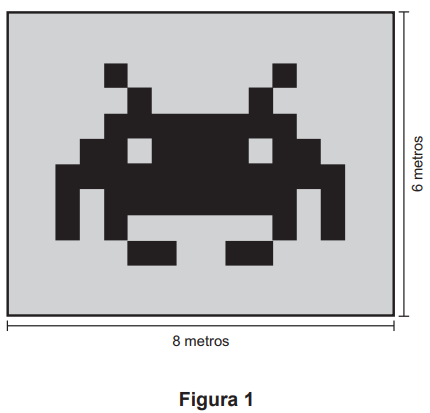
Deseja-se reproduzi-la numa folha de papel retangular com 42 cm de comprimento e 30 cm de altura, deixando livres 3 cm em cada margem, conforme a Figura 2.
A reprodução da gravura deve ocupar o máximo possível da região disponível, mantendo-se as proporções da Figura 1
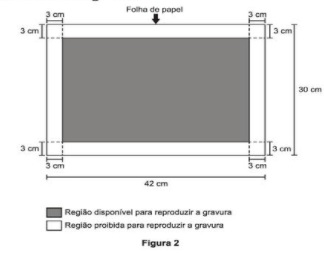
PRADO, A. C. Superinteressante, ed. 301, fev. 2012 (adaptado).
A escala da gravura reproduzida na folha de papel é:
A) 1 : 3.
B) 1 : 4.
C) 1 : 20.
D) 1 : 25.
E) 1 : 32.
Alternativa D
Sabemos que a figura 1 possui dimensões de 800 centímetros por 600 centímetros. Para encontrar as dimensões da folha, vamos subtrair o maior lado por 6, 42 – 6 = 36 cm e o menor lado também: 32 – 6 = 24. Para encontrar a proporção, vamos calcular a razão entre o tamanho real e o tamanho do desenho:
800 : 36 = 22 e 600 : 24 = 25
Escolhendo o maior deles, a escala será 1 : 25.