Exercícios sobre adição e subtração de polinômios
(EAM – Aprendiz de marinheiro) Analise a figura a seguir:
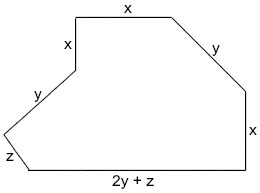
Suponha que o terreno comprado por um proprietário tenha a forma da figura acima e suas medidas sejam representadas, em unidades de comprimento, pelas variáveis X, Y e Z. A expressão algébrica que representa o perímetro desse terreno é:
a) 2x + 3y + z
b) 3x + 4y + 2z
c) 3x + 3y + z
d) 3x + 2y + 3z
e) 4x + 3y + 2z
Para determinamos a expressão algébrica que representa o perímetro, devemos somar todos os lados da figura geométrica que representa o terreno.
x + y + x + 2y + z + z + y + x =
Devemos agrupar os termos semelhantes, ou seja, os que possuem mesma variável.
= x + x + x + y + 2y + y + z + z =
Faça a redução dos termos semelhantes operando os coeficientes.
= 3 x + 4y + 2z
A expressão algébrica que representa o perímetro do terreno é a da alternativa “b”.
(EAM – Aprendiz de marinheiro) Reduzindo-se os termos semelhantes da expressão b(a - b) + (b + a) (b - a) - a(b - a) + (b - a)2, obtém-se:
a) (a – b)2
b) (a + b)2
c) b2 – a2
d) a2 – b2
e) a2 + b2
b(a - b) + (b + a) (b - a) - a(b - a) + (b – a)2 =
Efetue os produtos pela propriedade distributiva:
= ba – b2 + b2 – ab + ab – a2 – ab +a2 + b2 – 2ba + a2 =
Agrupe os termos semelhantes:
= ba – ab + ab – ab – 2ba – b2 + b2 + b2 – a2 +a2+ a2 =
Faça a redução dos termos semelhantes operando os coeficientes / números:
= - 2 ba + b2 + a2 =
Organizando os termos:
= + a2 - 2 ba + b2 =
Fatore a expressão:
= (a - b)2
A alternativa correta para essa questão é a letra “a”.
Resolva: (y2 + 4y – 5) + (– 3y2 + 12y – 1).
(y2 + 4y – 5) + (– 3y2 + 12y – 1) =
Tiremos os termos de dentro dos parênteses:
= y2 + 4y – 5 – 3y2 + 12y – 1 =
Agora agrupemos os termos semelhantes:
= y2 – 3y2 + 4y + 12y – 5 – 1 =
Basta reduzir os termos semelhantes operando os coeficientes / números.
= – 2y2 + 16y – 6
Subtraia x2 + 12x – 9 por – 8x2 + 7x – 1
(x2 + 12x – 9) - (– 8x2 + 7x– 1) =
Tiremos os termos de dentro dos parênteses fazendo o jogo de sinal para: - (– 8x2 + 7x– 1)
= x2 + 12x – 9 + 8x2 – 7x + 1 =
Agrupemos os termos semelhantes:
= X2 + 8x2 + 12x – 7x – 9 + 1 =
Basta reduzir os termos semelhantes operando os coeficientes / números.
= 9x2 + 5x - 8
