Exercícios sobre aplicações do Teorema de Pitágoras
Uma piscina olímpica tem formato retangular e possui 25 metros de largura e 50 metros de comprimento. Qual é a distância percorrida por um nadador que a atravessa diagonalmente?
Se a piscina possui formato retangular, os lados que medem 25 e 50 metros formam um ângulo reto entre si. O caminho diagonal traçado pelo nadador é a hipotenusa. Consideremos que d seja a distância percorrida pelo nadador. Pelo Teorema de Pitágoras, teremos:
d² = 25² + 50²
d² = 625 + 2500
d² = 3125
d = √3125
d = 25√5
Concluímos então que o nadador percorreu 25√5 metros em sua trajetória.
Imagine que você está no ponto vermelho indicado na figura a seguir e pretende chegar ao outro ponto sinalizado com “i”.
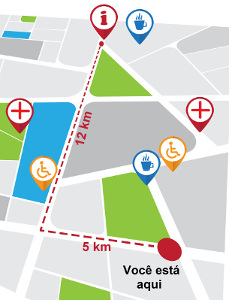
Supondo que o ângulo formado pelas ruas destacadas seja de 90°, se você não seguisse o caminho tracejado e fosse possível chegar ao seu destino através de uma linha reta, quantos quilômetros você percorreria?
Se o ângulo formado pelas ruas cujo caminho está tracejado for de 90°, teremos a formação de um ângulo reto, no qual as ruas são catetos e a linha reta entre o ponto de partida e o destino é a hipotenusa. Identificando a hipotenusa por h, pelo Teorema de Pitágoras, teremos:
h² = 5² + 12²
h² = 25 + 144
h² = 169
h = √169
h = 13
Uma linha reta entre o ponto que estamos e nosso destino mede exatamente 13 km.
(UFG) Uma pista retangular para caminhada mede 100 por 250 metros. Deseja-se marcar um ponto P, conforme figura a seguir, de modo que o comprimento do percurso ABPA seja a metade do comprimento total da pista. Calcule a distância entre os pontos B e P.
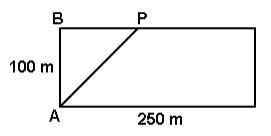
Observe na imagem a seguir as medidas x e y que precisamos identificar:
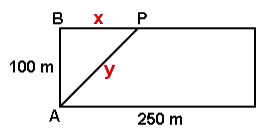
Se o objetivo é que o comprimento de ABPA seja a metade do comprimento total da pista, isso é o mesmo que afirmarmos que:
AB + BP + PA = (100 + 100 + 250 + 250)
2
100 + x + y = 350
x + y = 350 – 100
x + y = 250
y = 250 – x
A intenção é determinar o valor do comprimento BP = x. Para isso, em vez de utilizar PA = y, utilizaremos PA = 250 – x para que tenhamos uma única variável. Aplicaremos o Teorema de Pitágoras no triângulo retângulo ABPA para descobrir o valor de x:
(PA)² = (AB)² + (BP)²
(250 – x)² = 100² + x²
62500 – 500x + x² = 10000 + x²
– 500x = 10000 – 62500
– 500x = – 52500
500x = 52500
x = 52500
500
x = 105
Portanto, o comprimento BP vale 105 metros.
(Fuvest) No quadrilátero ABCD da figura a seguir, E é um ponto sobre o lado AD tal que o ângulo ABE mede 60º e os ângulos EBC e BCD são retos. Sabe-se ainda que AB = CD = √3 e BC = 1. Determine a medida de AD.
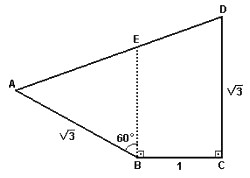
Primeiramente, observe na figura a seguir que podemos traçar o triângulo BCD:
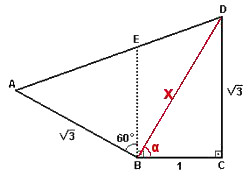
Através do Teorema de Pitágoras, podemos determinar o comprimento do lado BD = x:
(BD)² = (BC)² + (CD)²
x² = 1² + (√3)²
x² = 1 + 3
x = √4
x = 2
Vamos verificar a medida do ângulo α formado pelos segmentos de reta BD e BC através da fórmula da tangente:
tg α = cateto oposto a α
cateto adjacente a α
tg α = √3
1
tg α = √3
α = 60°
Se na primeira figura o ângulo formado pelos segmentos EB e BC mede 90°, o ângulo formado por EB e BD é de 30°, o que nos garante que o triângulo ABD é retângulo, como podemos ver na figura a seguir:
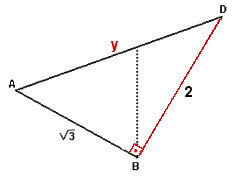
Aplicando novamente o Teorema de Pitágoras:
(AD)² = (AB)² + (BD)²
y² = (√3)² + 2²
y² = 3 + 4
y = √7
Portanto, o lado AD mede √7.
