Exercícios sobre Aplicações do Teorema de Tales
Sabendo que as retas a, b e c são paralelas, utilize o Teorema de Tales e determine o valor de x na figura a seguir:
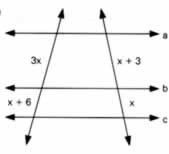
Pelo Teorema de Tales temos que: 
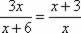. Aplicando a propriedade das proporções, na igualdade entre as razões, determinaremos o valor de x, veja: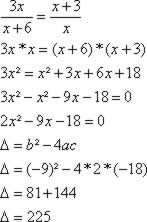
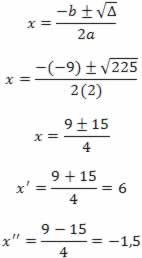
Como o valor de x'' = - 1,5 não é interessante para nós, o único valor possível de x que satisfaz a proporção é x' = 6.
Na figura a seguir temos que a // b // c // d. Aplicando o Teorema de Tales determine os valores de x, z e y.
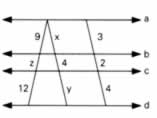
Pelo Teorema de Tales temos que:
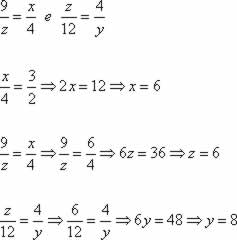
Solução: x = 6, z = 6 e y = 8.
Aplique o Teorema de Tales no intuito de determinar o valor de x, sabendo que as retas a, b e c são paralelas.
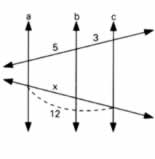
De acordo com o Teorema de Tales temos:
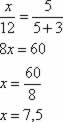
O valor de x de acordo com o Teorema de Tales é 7,5.
(Fuvest–SP) Três terrenos têm frente para a rua A e para a rua B, como na figura. As divisas laterais são perpendiculares à rua A. Qual a medida de frente para a rua B de cada lote, sabendo que a frente total para essa rua tem 180m?
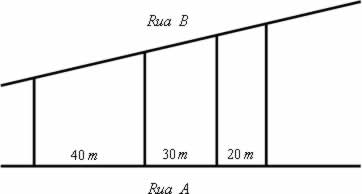
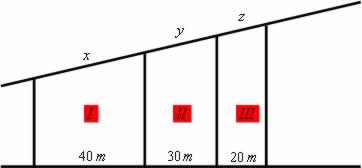
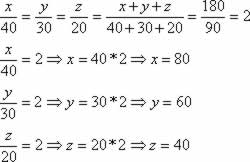
Lote I: 80 metros
Lote II: 60 metros
Lote III: 40 metros
(Saresp–SP) No desenho abaixo estão representados os terrenos I, II e III.
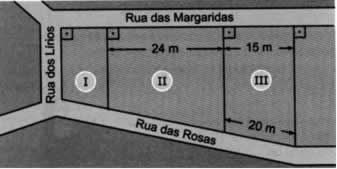
Quantos metros de comprimento deverá ter o muro que o proprietário do terreno II construirá para fechar o lado que faz frente com a Rua das Rosas?
.exercicios.jpg)
Aplicando o Teorema de Tales temos a seguinte situação:
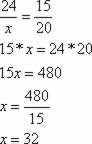
O muro do terreno II que faz frente com a Rua das Rosas deverá ter 32 metros de comprimento.
(Fuvest–SP) A sombra de um poste vertical, projetada pelo sol sobre um chão plano, mede 12 m. Nesse mesmo instante, a sombra, de um bastão vertical de 1 m de altura mede 0,6 m. Qual a altura do poste?
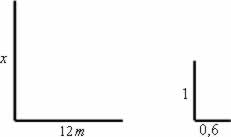
De acordo com o Teorema de Tales: x = 1
12 0,6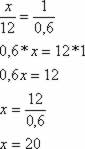
A altura do poste é correspondente a 20 metros.
