Exercícios sobre a área da coroa circular
Qual a área da parte laranja da figura abaixo, sabendo que ela é formada por dois círculos concêntricos, um de raio 10 cm e outro de raio 15 cm? Considere π = 3,14.
a) 78,5 cm
b) 178,5 cm
c) 292,5 cm
d) 392,5 cm
e) 478,5 cm
Pode-se usar a fórmula a seguir:
A = π(R2 – r2)
Ou calcular a área das duas circunferências e subtrair a área da menor da área da maior. Optamos pelo primeiro método:
A = 3,14·(152 – 102)
A = 3,14·(225 – 100)
A = 3,14·(125)
A = 392,5 cm2
Alternativa D
Um círculo de raio 20 cm servirá como base de corte para um novo círculo, concêntrico a ele, que deverá ter área igual a 310 cm2. Qual a área será descartada do primeiro círculo? Considere π = 3,1.
a) 930 cm2
b) 950 cm2
c) 1000 cm2
d) 310 cm2
e) 620 cm2
Existem dois círculos concêntricos. O menor tem área igual a 310 cm2, e o segundo raio 20 cm. Para descobrir a área da coroa circular externa ao círculo menor, que é a parte do círculo maior que será descartada, podemos seguir uma das duas estratégias:
Descobrir a medida do raio do círculo menor, uma vez que possuímos a medida de sua área, e substituir as medidas dos dois raios na fórmula:
A = π(R2 – r2)
Ou calcular a área do círculo maior e subtrair as duas áreas. Optamos pela segunda alternativa:
A1 = 310 cm2
A2 = πr2
A2 = 3,1·202
A2 = 3,1·400
A2 = 1240 cm2
A2 – A1 = 1240 – 310 = 930 cm2
Alternativa A
Um fazendeiro resolveu marcar seus tratores pintando os pneus, apenas pelo lado de fora, com uma tinta vermelha. Sabendo que o metro quadrado de tinta custa R$ 1,20, que o fazendeiro pintou 4 pneus e que a parte pintada de cada pneu representa uma coroa circular com raio menor igual a 1 metro e o raio maior igual a 1,5 metros, quanto esse fazendeiro gastou com tinta? Considere π = 3,1
a) R$ 10,60
b) R$ 12,60
c) R$ 14,60
d) R$ 15,60
e) R$ 18,60
Primeiramente, será necessário encontrar a área que será pintada de cada pneu.
A = π(R2 – r2)
A = 3,1(1,52 – 12)
A = 3,1(2,25 – 1)
A = 3,1(1,25)
A = 3,875 m2
A área de 4 pneus será:
4A = 4·3,875 = 15,5 m2
E o valor da tinta será:
15,5·1,2 = R$ 18,60
Alternativa E
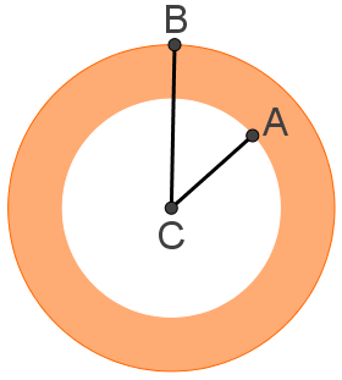
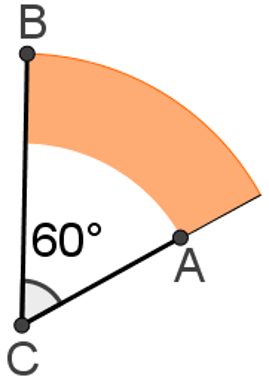
Na figura a seguir, o comprimento do segmento CA é 8 cm, e o comprimento do segmento CB é 10 cm. Qual é a área da figura laranja sabendo que ela é parte de uma coroa circular? Considere π = 3,1.
a) 18,6 cm2
b) 54,6 cm2
c) 111,6 cm2
d) 120,3 cm2
e) 200 cm2
Observe que o ângulo dos arcos nessa figura é igual a 60°. Significa que, por regra de três, determinando a área da coroa circular, poderemos determinar também a área dessa figura.
A1 = π(R2 – r2)
A1 = 3,1(102 – 82)
A1 = 3,1(100 – 64)
A1 = 3,1(36)
A1 = 111,6 cm2
Essa é a área da coroa circular completa, que equivale a 360°. Por regra de três, teremos:
111,6 = 360
x 60
360x = 111,6·60
360x = 6696
x = 6696
360
x = 18,6 cm2
Alternativa A
