Exercícios sobre baricentro
Esta lista é composta de questões sobre o baricentro de um triângulo, que é o encontro de suas medianas, conhecido também como centro de gravidade do triângulo.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
O triângulo possui importantes pontos notáveis, sendo eles o baricentro, incentro, ortocentro e circuncentro. Sobre o baricentro, podemos afirmar que ele é o ponto de encontro das(os):
A) alturas.
B) bissetrizes.
C) mediatrizes.
D) medianas.
E) vértices.
Alternativa D
O baricentro é, por definição, o ponto em que ocorre o encontro das medianas de um triângulo.
-
Questão 2
Sobre o baricentro, julgue as afirmativas a seguir:
I → O baricentro é sempre um ponto interno do triângulo.
II → O baricentro é o ponto de encontro das mediatrizes.
III → O baricentro é equidistante dos vértices do triângulo.
Marque a alternativa correta.
A) Somente I é verdadeira.
B) Somente II é verdadeira.
C) Somente III é verdadeira.
D) Somente I e III são verdadeiras.
E) Todas são verdadeiras.
Alternativa A
I → Verdadeira
Uma das propriedades do baricentro é ser sempre um ponto interno do triângulo.
II → Falsa
O baricentro é o ponto de encontro das medianas, e não das mediatrizes.
III → Falsa
O baricentro não é necessariamente equidistante dos vértices.
-
Questão 3
Um triângulo foi representado no plano cartesiano com vértices nos pontos A(– 1, – 2), B(3, 5) e C(4, – 3). Podemos afirmar que o seu baricentro é o ponto
A) G(0, 2).
B) G(6, 0).
C) G(2, 0).
D) G(1, 3).
E) G(– 1, – 3).
Alternativa C
De início, encontraremos o valor de xG:
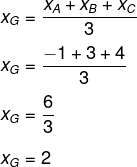
Agora, calcularemos o valor de yG:
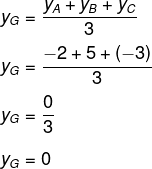
Portanto, as coordenadas do baricentro são G(2, 0).
-
Questão 4
Em um triângulo, foram traçadas as medianas, como na imagem a seguir:
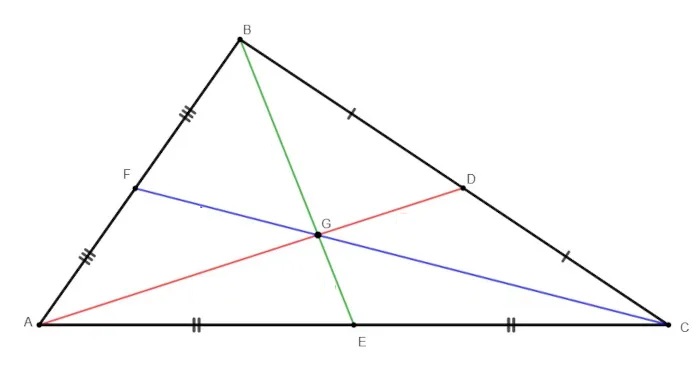
Conhecendo os valores dos seguintes comprimentos de segmentos: AC = 48 cm, BE = 24 cm e AD = 30 cm, pode-se afirmar que o perímetro do triângulo AGE é igual a
A) 18 cm.
B) 24 cm.
C) 32 cm.
D) 48 cm.
E) 52 cm.
Alternativa E
Queremos encontrar as medidas AE, EG e AG. Começando por AE, temos em mente que E é o ponto médio de AC. Dessa forma, o comprimento de AE é a metade do comprimento de AC.
AE = 48 : 2
AE = 24 cm
Analisando a mediana BE, descobrimos que EG é o menor segmento da mediana. Logo, ele mede 1/3 do valor dela. Então, o comprimento de EG é igual ao comprimento de BE dividido por 3.
EG = 24 : 3 = 8 cm
Para encontrar o último comprimento, perceba que AG é o maior segmento maior da mediana AD. Sendo assim, seu comprimento equivale a 2/3 do comprimento de AD. Dessa forma, temos que:
AG = 2/3 ⸳ 30
AG = 60/3
AG = 20 cm
Por fim, o perímetro do triângulo AEG é igual a:
P = 24 + 8 + 20 = 52 cm
-
Questão 5
Em uma investigação sobre lavagem de dinheiro feita pela Polícia Federal, foram implantadas três escutas em uma sala onde aconteceria uma reunião entre empresários. Um grupo de inteligência dividiu a sala em um plano cartesiano, e os pontos escolhidos para a instalação das escutas foram A(7, 2), B(5, 6) e C(0, 1). Durante os testes, verificou-se que a captação de áudio não estava totalmente calibrada. Por causa disso, foi adicionada uma nova escuta, no ponto P, baricentro do triângulo A, B e C. Conclui-se que a quarta escuta ficou localizada no ponto
A) (12, 9).
B) (9, 12).
C) (4, 3).
D) (3, 4).
E) (5, 6).
Alternativa C
Sabemos que o ponto P é baricentro do triângulo A, B e C. Calculando a média dos valores para x nesses pontos, temos que:
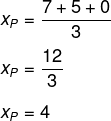
Agora, calculando a média entre os valores para y, temos que:
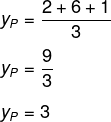
Logo, as coordenadas do ponto P são (4, 3).
-
Questão 6
Os pontos A(2, 3), B(– 1, 4) e C(x, y) são vértices de um triângulo cujo baricentro é o ponto G(0, 3). A soma de x + y é igual a
A) 1.
B) 2.
C) 3.
D) 4.
E) 5.
Alternativa A
Nesse caso, conhecemos as coordenadas de 2 vértices do triângulo e de seu baricentro. Substituindo na fórmula para encontrar a abscissa do baricentro, calcula-se o seguinte:
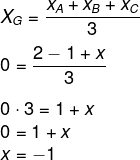
Substituiremos na fórmula para calcular a coordenada do baricentro:
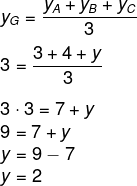
Por fim, a soma x + y = – 1 + 2 = 1.
-
Questão 7
Em uma fazenda, estão sendo instaladas três torres de comunicação para ajudar na análise e acompanhamento das plantações. As três torres são vértices do triângulo A, B e C. Para escolher a posição das torres, definiram que a casa da fazenda ficará no ponto (1, – 1) e que, por motivos técnicos, ela deve ser o baricentro do triângulo ABC. Sabendo que as localizações das torres A e B são A(12, – 6) e B(– 4, – 10), qual deve ser a localização da torre C?
A) (8, – 4).
B) (5, – 13).
C) (3, 8).
D) (– 5, 13).
E) (– 5, 8).
Alternativa D
Sabe-se que G é a localização do centro do triângulo, que é o ponto das coordenadas (1, – 1).
Sendo (x, y) as coordenadas do ponto C, temos o seguinte cálculo:
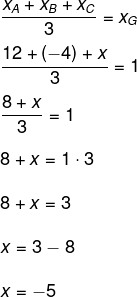
Devemos encontrar, também, o valor de y:
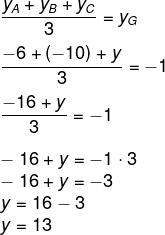
Então, temos que C(– 5, 13).
-
Questão 8
Durante seus estudos de Geometria, Laís fez o desenho de um triângulo e traçou as suas três medianas. Quando assim o fez, ela percebeu que elas se encontram em um único ponto. Esse ponto é um dos pontos notáveis do triângulo, conhecido como
A) baricentro.
B) circuncentro.
C) incentro.
D) ortocentro.
Alternativa A
O ponto de encontro das medianas é conhecido como baricentro.
-
Questão 9
(Fauel) O baricentro de um triângulo divide a mediana em duas partes, sendo que a parte que contém o vértice é o dobro do tamanho da que contém o ponto médio. Assinale a alternativa correspondente às coordenadas do vértice B do triângulo ABC, sendo que seu baricentro possui coordenadas G(3, 4) e que os outros dois vértices são A(2, 7) e C(3, 2).
A) B(1, 3).
B) B(4, 3).
C) B(2, 4).
D) B(7, 3).
Alternativa B
Queremos encontrar as coordenadas do ponto B. Substituindo os valores dados na fórmula para encontrar as coordenadas do baricentro, temos que:
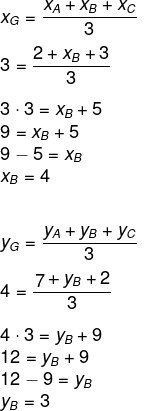
Conclui-se que o ponto B possui coordenadas (4, 3).
-
Questão 10
Sobre o baricentro de um triângulo, podemos afirmar que:
A) ele é um ponto equidistante aos vértices.
B) ele é o centro de gravidade de um triângulo.
C) ele é o ponto de encontro de suas alturas.
D) ele é o segmento de reta que liga as medianas.
Alternativa B
O baricentro é conhecido também como o centro de gravidade de um triângulo.
-
Questão 11
(ITA) Sejam A = (0, 0), B = (0, 6) e C = (4, 3) vértices de um triângulo, a distância do baricentro desse triângulo ao vértice A, em unidades de distância, é igual a:
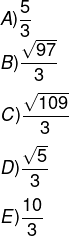
Alternativa B
Encontrando primeiro as coordenadas do baricentro:
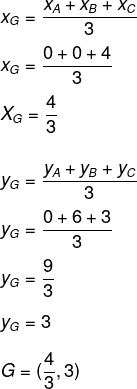
Agora, calculando a distância entre os pontos A e G:
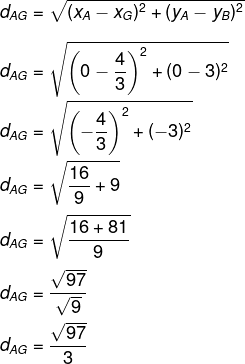
-
Questão 12
(Seduc) O baricentro de uma área plana é o ponto no qual está localizado o centro de gravidade da área considerada. Na Matemática, define-se o baricentro de uma área limitada por um triângulo como sendo o ponto de interseção das medianas do triângulo. Se no plano cartesiano os pontos (1, 6) e (3, 2) são vértices de um triângulo cujo baricentro é o ponto (5/3, 3), então o terceiro vértice desse triângulo é o ponto
A) (2/3, 1).
B) (1, 1).
C) (1, 4/3).
D) (2/3, 4/3).
E) (1, 2/3).
Alternativa B
Sejam A(1, 6), B(3, 2) e C(x, y), sabendo também que G(5/3, 3), para encontrar o valor de x, temos que:
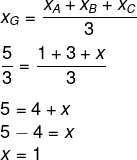
Calcularemos, agora, o valor de y:
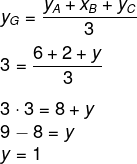
O ponto C possui, então, coordenadas (1, 1).