Exercícios sobre circunferência
Na fazendo do Seu Sebastião, o cultivo de milho é feito em uma área delimitada por uma circunferência. Para evitar invasões de animais na plantação, ele decidiu cercá-la com arame farpado, dando 4 voltas completas. Sabendo que o diâmetro da circunferência é de 1 km, a quantidade mínima de arame necessária para cercar essa área é igual a:
(Use π = 3)
A) 3 km
B) 6 km
C) 12 km
D) 20 km
E) 24 km
Alternativa C
Queremos calcular o comprimento da circunferência. Como o diâmetro é de 1 km, o raio será de 0,5 km, que é igual a 500 metros.
C = 2πr
C = 2 · 3 · 0,5
C = 3 km
Como ele deseja 4 voltas, então são necessários 4 · 3 = 12 km de arame, no mínimo.
Sobre a circunferência, julgue as afirmativas a seguir:
I → A circunferência de centro O e raio r é um conjunto de todos os pontos cuja distância até O é igual a r.
II → O comprimento do diâmetro é sempre igual à metade do comprimento do raio.
III → A circunferência é uma área plana limitada por um círculo.
Marque a alternativa correta:
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Todas as afirmativas são falsas.
Alternativa A
I → Verdadeira
A circunferência de centro O e raio r é o conjunto de todos os pontos cuja distância até O é igual a r. Essa é a definição de circunferência.
II → Falsa
O comprimento do diâmetro é o dobro do comprimento do raio.
III → Falsa
O círculo é a área plana limitada pela circunferência, e não o contrário.
A circunferência c foi representada em uma malha quadriculada, sendo que A é o ponto que representa seu centro.
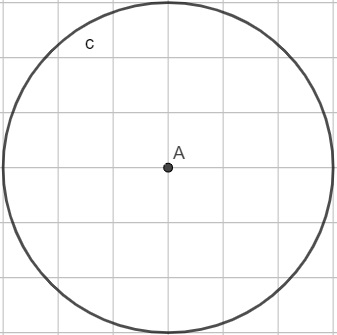
Analisando a figura, podemos afirmar que a área delimitada pela circunferência é igual a:
(Use π = 3)
A) 30 u.a.
B) 27 u.a.
C) 18 u.a.
D) 15 u.a.
E) 12 u.a.
Alternativa B
A partir da imagem, percebemos que a circunferência possui raio igual a 3 unidades de medida (u.m.)
Então, a sua área é igual a:
A = πr²
A = 3 · 3²
A = 3 · 9
A = 27 unidades de área (u.a.)
Analise a circunferência a seguir:
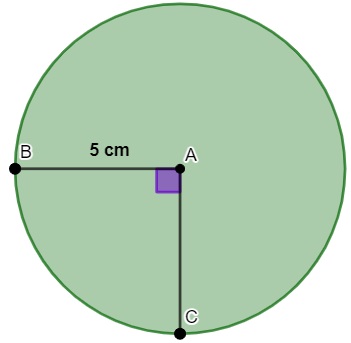
Podemos afirmar que o comprimento do arco BC é igual a:
(Use π = 3)
A) 7,5 cm
B) 15 cm
C) 20 cm
D) 22,5 cm
E) 30 cm
Alternativa A
Primeiramente, calcularemos o comprimento dessa circunferência:
C = 2πr
C = 2 · 3 · 5
C = 30 cm
Note que o ângulo BAC possui 90°. Logo, o arco BC equivale a um quarto do comprimento da circunferência. Assim, o comprimento do arco é de 30 : 4 = 7,5 cm.
Dentro das cozinhas, é bastante comum que seja utilizada a panela de pressão, que possui em sua tampa um elástico, com objetivo de evitar a saída do vapor e acelerar o processo de cozimento. Suponha que uma panela possui uma tampa totalmente circular, com 6 cm de raio. O comprimento do elástico dessa tampa deve ser igual a:
(Use π = 3,1)
A) 34,9 cm
B) 35,0 cm
C) 35,4 cm
D) 36,6 cm
E) 37,2 cm
Alternativa E
Sabemos que:
r = 6
π = 3,1
Calculando o comprimento, temos:
C = 2πr
C = 2 · 3,1 · 6
C = 6,2 · 6
C = 37,2 cm
(Enem 2014 – PPL) Um homem, determinado a melhorar sua saúde, resolveu andar diariamente numa praça circular que há em frente à sua casa. Todos os dias ele dá exatamente 15 voltas em torno da praça, que tem 50 m de raio.
Qual é a distância percorrida por esse homem em sua caminhada diária?
(Use π = 3,0)
A) 0,30 km
B) 0,75 km
C) 1,50 km
D) 2,25 km
E) 4,50 km
Alternativa E
Inicialmente, calcularemos a distância percorrida pelo homem ao dar uma volta:
C = 2πr
C = 2 · 3 · 50
C = 300 m
Como ele dá 15 voltas, a distância percorrida em metros será de:
300 · 15 = 4500 metros
Convertendo para km, 4500 m = 4,5 km.
(IFG 2019) Se o raio R de uma circunferência for reduzido pela metade, é correto afirmar que:
A) O valor da área círculo ficará reduzida pela metade do valor da área do círculo inicial de raio R.
B) O valor da área do círculo ficará a ¾ do valor da área do círculo inicial de raio R.
C) O comprimento da circunferência se reduzirá a ¼ do valor do comprimento da circunferência inicial de raio R.
D) O comprimento da circunferência se reduzirá à metade do valor do comprimento da circunferência inicial de raio R.
Alternativa D
Se o raio for divido pela metade, obteremos r : 2.
Analisando as alternativas, verificaremos a redução na área e no comprimento.
Sabemos que a área é A = πr². Se o raio for reduzido pela metade, teremos:
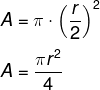
Logo, a área será ¼ da área anterior, o que faz com que as alternativas A e B sejam falsas.
Calculando o comprimento, temos:
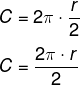
Note que o comprimento foi reduzido pela metade, o que faz com que a alternativa D seja a correta.
(IFG 2015) Dois círculos, C1 e C2, possuem raios com medidas 3x e x+5, em cm, respectivamente. Sabe-se que a razão entre o comprimento de C1 e o comprimento de C2 é igual a 2. Dessa forma, é correto afirmar que as áreas de C1 e C2 valem em cm², respectivamente:
(use π = 3,14)
A) 900 π e 225 π.
B) 920 π e 240 π.
C)905 π e 255 π.
D) 910 π e 235 π.
Alternativa A
Sabemos que a razão entre o comprimento do círculo C1 e do C2 é igual a 2 e que r1 = 3x e r2 = x + 5:
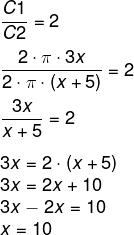
Calculando a área do círculo C1:
A1 = πr²
A1 = π (3x)²
Como x = 10, então:
A1 = π · (3 · 10)²
A1 = π · 30²
A1 = 900π
Agora, calcularemos A2:
A2 = πr²
A2 = π (x + 5)²
Como x = 10, calculamos:
A2 = π · (10 + 5)²
A2 = π · 15²
A2 = 225π
As áreas são, respectivamente, 900π cm² e 225π cm².
(Enem 2019) Em um condomínio, uma área pavimentada, que tem a forma de um círculo com diâmetro medindo 6 m, é cercada por grama. A administração do condomínio deseja ampliar essa área, mantendo seu formato circular e aumentando, em 8 m, o diâmetro dessa região, mantendo o revestimento da parte já existente. O condomínio dispõe, em estoque, de material suficiente para pavimentar mais 100 m² de área. O síndico do condomínio avaliará se esse material disponível será suficiente para pavimentar a região a ser ampliada.
A conclusão correta a que o síndico deverá chegar, considerando a nova área a ser pavimentada, é a de que o material disponível em estoque:
(Use π = 3)
A) será suficiente, pois a área da nova região a ser pavimentada mede 21 m².
B) será suficiente, pois a área da nova região a ser pavimentada mede 24 m².
C) será suficiente, pois a área da nova região a ser pavimentada mede 48 m².
D) não será suficiente, pois a área da nova região a ser pavimentada mede 108 m².
E) não será suficiente, pois a área da nova região a ser pavimentada mede 120 m².
Alternativa E
A área inicialmente possuía um raio de 3 metros. Como o diâmetro será aumentado em 8m, essa região terá 14 metros de diâmetro, ou seja, 7 metros de raio. Calculando a diferença entre essas áreas:
A1= πr² = 3 · 3² = 27 m²
A2 = πr² = 3 · 7² = 147 m²
147 – 27 = 120 m²
Logo, a quantidade de material não será suficiente, pois a área da nova região a ser pavimentada mede 120 m².
Em uma fábrica de embalagens, a tampa de determinado produto possui área igual a 78,5 cm². Sabendo que ele possui formato circular e utilizando 3,14 como aproximação para π, o raio dessa tampa é igual a:
A) 5 cm
B) 6 cm
C) 8 cm
D) 9 cm
E) 10 cm
Alternativa A
Sabendo que A = πr², calculamos:
78,5 = 3,14 · r²
78,5 : 3,14 = r²
25 = r²
r = √25
r = 5 cm
Sobre a circunferência, julgue as afirmativas a seguir.
I → O diâmetro é um segmento de reta que liga uma extremidade a outra da circunferência, passando pelo centro.
II → A corda é um segmento de reta que liga um ponto da circunferência ao seu centro.
III → A medida do raio da circunferência é sempre igual à metade da medida do seu diâmetro.
Marque a alternativa correta:
A) Somente a afirmativa I é falsa.
B) Somente a afirmativa II é falsa.
C) Somente a afirmativa III é falsa.
D) Toda as afirmativas são verdadeiras.
Alternativa B
I → Verdadeira
A definição de diâmetro está correta.
II → Falsa
O segmento que liga um ponto da circunferência ao centro é o raio, e não a corda.
III → Verdadeira
Para encontrar o comprimento do raio, basta dividir o diâmetro por dois.
Um parque possui formato circular e será cercado para a realização de um evento. Sabendo que para cercar essa região será gasto um total de R$ 9,00 por metro e que o raio desse parque é de 14 metros, o valor gasto para cercá-lo será igual a:
(Use π = 3)
A) R$ 756,00
B) R$ 695,00
C) R$ 640,00
D) R$ 525,00
E) R$ 490,00
Alternativa A
Primeiramente, calcularemos o comprimento do parque:
C = 2πr
C = 2 ·3 · 14
C = 84 m
Como serão gastos R$ 9,00 por metro, o valor total será de 84 · 9 = R$ 756,00.
