Exercícios sobre desvio-padrão
O desvio-padrão do conjunto {2, 4, 8, 12, 16} é igual a aproximadamente:
A) 6,0
B) 6,2
C) 6,4
D) 6,6
E) 6,9
Alternativa B
Para encontrar o desvio-padrão, primeiro calcularemos a média:
\(\overline{x}=\frac{2+4+8+12+19}{5}\)
\(\overline{x}=\frac{45}{5}\)
\(\overline{x}=9\)
Agora calcularemos o desvio-padrão:
\(DP=\sqrt{\frac{\left(2-9\right)^2+\left(4-9\right)^2+\left(8-9\right)^2+\left(12-9\right)^2+\left(19-9\right)^2}{5}}\)
\(DP=\sqrt{\frac{\left(-7\right)^2+\left(-5\right)^2+\left(-1\right)^2+\left(4\right)^2+\left(10\right)^2}{5}}\)
\(DP=\sqrt{\frac{49+25+1+16+100}{5}}\)
\(DP=\sqrt{\frac{191}{5}}\)
\(DP=\sqrt{38,2}\)
\(DP\cong6,2\)
Durante um congresso de professores, as mesas eram compostas por 5 pessoas. Foi feita uma competição em que o grupo vencedor seria aquele que possuísse um conjunto de idades mais homogêneo. A idade de cada um dos membros do grupo está listada na tabela a seguir:
|
|
|
|
|
|
|
Média |
σ |
|
Grupo 1 |
28 |
25 |
19 |
41 |
32 |
29 |
7,3 |
|
Grupo 2 |
19 |
20 |
37 |
35 |
45 |
31,2 |
10,1 |
|
Grupo 3 |
55 |
28 |
32 |
37 |
19 |
34,2 |
12,0 |
|
Grupo 4 |
31 |
33 |
39 |
36 |
40 |
35,8 |
3,4 |
|
Grupo 5 |
36 |
22 |
38 |
29 |
24 |
29,8 |
6,3 |
A grupo vencedor foi:
A) grupo 1
B) grupo 2
C) grupo 3
D) grupo 4
E) grupo 5
Alternativa D
O grupo mais homogêneo é aquele que possui menor desvio-padrão; no caso, é o grupo 4.
Durante as aulas de história, o professor separou os estudantes em grupos de 3 alunos para uma competição e anotou a nota de cada grupo na tabela seguir:
|
|
Nota 1 |
Nota 2 |
Nota 3 |
|
Grupo 1 |
6 |
8 |
4 |
|
Grupo 2 |
4 |
6 |
5 |
|
Grupo 3 |
8 |
8 |
5 |
|
Grupo 4 |
7 |
9 |
6 |
|
Grupo 5 |
6 |
6 |
6 |
Na competição, o grupo vencedor seria aquele que tivesse maior média de notas. Caso haja empate, o critério é o grupo que possui notas mais regulares. Analisando as notas dos grupos na tabela, o grupo vencedor foi:
A) grupo 1
B) grupo 2
C) grupo 3
D) grupo 4
E) grupo 5
Alternativa D
Primeiro calcularemos a média de cada grupo:
\(\overline{x_1}=\frac{6+8+4}{3}=\frac{18}{3}=6\)
\(\overline{x_2}=\frac{4+6+5}{3}=\frac{15}{3}=5\)
\(\overline{x_3}=\frac{8+8+5}{3}=\frac{21}{3}=7\)
\(\overline{x_4}=\frac{7+8+6}{3}=\frac{21}{3}=7\)
\(\overline{x_5}=\frac{6+6+6}{3}=\frac{18}{3}=6\)
Podemos perceber que o grupo 3 e o grupo 4 possuem maior média, agora, é necessário calcular o desvio-padrão desses grupos para saber qual grupo é o mais regular.
\(DP_3=\sqrt{\frac{\left(8-7\right)^2+\left(8-7\right)^2+\left(5-7\right)^2}{3}}\)
\(DP_3=\sqrt{\frac{1^2+1^2+\left(-2\right)^2}{3}}\)
\(DP_3=\sqrt{\frac{1+1+4}{3}}\)
\(DP_3=\sqrt{\frac{6}{3}}\)
\(DP_3=\sqrt2\)
\(DP_4=\sqrt{\frac{\left(7-7\right)^2+\left(8-7\right)^2+\left(6-7\right)^2}{3}}\)
\(DP_4=\sqrt{\frac{0^2+1^2+1^2}{3}}\)
\(DP_4=\sqrt{\frac{1+1}{3}}\)
\(DP_4=\sqrt{\frac{2}{3}}\)
Sabemos que o desvio-padrão do grupo 4 é menor que o desvio-padrão do grupo 3, logo, o vencedor é o grupo 4.
Durante a coleta de dados, um estatístico percebeu que os dados do grupo A possuem desvio-padrão igual a 2, já o grupo B possui desvio-padrão igual a 1. Conhecendo o desvio-padrão, podemos afirmar que a soma das variâncias dos conjuntos A e B é igual a:
A) 3
B) 4
C) 5
D) 6
E) 7
Alternativa C
Sabemos que o desvio-padrão é igual à raiz quadrada da variância, então, para encontrar a variância de cada um dos grupos, basta elevar o desvio-padrão encontrado ao quadrado.
2² = 4
1² = 1
A soma desses valores é igual a 4 + 1 = 5.
Sobre o desvio-padrão, foram feitas as seguintes afirmativas:
I. Quanto maior for o desvio-padrão de um conjunto, mais regulares serão os dados desse conjunto.
II. Quanto menor for o desvio-padrão de um conjunto, mais homogêneos serão os dados desse conjunto.
III. Se o desvio-padrão for igual a zero, o conjunto possui todos os valores iguais.
Analisando as afirmativas, podemos afirmar que:
A) Somente a afirmativa I está incorreta.
B) Somente a afirmativa II está incorreta.
C) Somente a afirmativa III está incorreta.
D) Todas as afirmativas estão corretas.
E) Todas as afirmativas estão incorretas.
Alternativa A
I) Quanto maior for o desvio-padrão de um conjunto, mais regulares serão os dados desse conjunto. (Falsa)
Quanto maior for o desvio-padrão, menos regulares serão os dados do conjunto.
II) Quanto menor for o desvio-padrão de um conjunto, mais homogêneos serão os dados desse conjunto. (Verdadeira)
De fato, quanto menor for o desvio-padrão, mais homogêneos serão os dados do conjunto.
III) Se o desvio-padrão for igual a zero, o conjunto possui todos os valores iguais. (Verdadeira)
Quando o dsvio-padrão é igual a 0, significa que não há variação nos dados do conjunto.
Durante as aulas de Matemática, o professor Raul percebeu uma diferença entre as notas da turma A e da turma B de uma mesma série.
Turma A – média = 8,0 e desvio-padrão = 1,0
Turma B – média = 8,5 e desvio-padrão = 2,0
Analisando esses resultados, o professor pode afirmar que:
A) A maior nota está na turma A.
B) A maior nota está na turma B.
C) A turma A possui notas mais regulares.
D) A turma B possui notas mais regulares.
E) A turma B possui as menores notas.
Alternativa C
Como o desvio-padrão da turma A é maior, então podemos afirmar que a turma A possui notas mais regulares.
Na academia, o instrutor mediu a altura das suas alunas em metros e coletou os seguintes dados:
Marcela 1,67
Kárita 1,70
Júlia 1,68
Natália 1,63
O desvio-padrão das alturas coletadas é igual a aproximadamente:
A) 0,0025
B) 0,0032
C) 0,0037
D) 0,0045
E) 0,0052
Alternativa A
Primeiro calcularemos a média:
\(\overline{x}=\frac{1,67+1,70+1,68+1,63}{4}=\frac{6,68}{4}=1,67\)
Sabendo que a média é 1,67, temos que:
\(DP=\sqrt{\frac{\left(1,67-1,67\right)^2+\left(1,70-1,67\right)^2+\left(1,68-1,67\right)^2+\left(1,63-1,67\right)^2}{4}}\)
\(DP=\sqrt{\frac{0^2+{0,03}^2+{0,01}^2+\left(-0,04\right)^2}{4}}\)
\(DP=\sqrt{\frac{0+0,0009+0,0001+0,0016}{4}}\)
\(DP=\sqrt{\frac{0,0026}{4}}\)
\(DP=\sqrt{0,00065}\)
\(DP=0,025\)
Durante as aulas de Matemática, o professor escolheu um grupo de 10 estudantes da sala para calcular o desvio-padrão do número de irmãos que cada aluno tinha. Após coletar esses dados, o professor calculou que a média era 1 e o desvio-padrão era igual a 0, então podemos afirmar que:
A) A quantidade de irmãos que cada um desses 10 alunos possui é muito próxima, com uma variação muito pequena.
B) O número total de irmãos é igual ao número de alunos, podendo haver alunos que têm 2 irmãos e alunos que não têm nenhum irmão por exemplo.
C) Todos os estudantes são filhos únicos, logo, nenhum deles tem irmão.
D) Todos os 10 estudantes consultados têm exatamente 1 irmão, por isso, a média é 1.
Alternativa D
Como o desvio-padrão é 0, significa que todos os dados são iguais no conjunto, ou seja, não há variação. Sabendo que a média é 1, então cada um dos estudantes tem 1 único irmão.
(Enem – PPL) Em uma corrida de regularidade, a equipe campeã é aquela em que o tempo dos participantes mais se aproxima do tempo fornecido pelos organizadores em cada etapa. Um campeonato foi organizado em 5 etapas, e o tempo médio de prova indicado pelos organizadores foi de 45 minutos por prova. No quadro, estão representados os dados estatísticos das 5 equipes mais bem classificadas.
Dados estatísticos das equipes mais bem classificadas (em minutos):
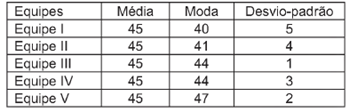
Utilizando os dados estatísticos do quadro, a campeã foi a equipe:
A) I
B) II
C) III
D) IV
E) V
Alternativa C
A equipe que menos se distanciou da média é a que possui desvio-padrão menor. Analisando a tabela, podemos afirmar que a equipe III é a campeã.
(Enem 2019 – PPL) Um fiscal de certa empresa de ônibus registra o tempo, em minutos, que um motorista novato gasta para completar certo percurso. No Quadro 1 figuram os tempos gastos pelo motorista ao realizar o mesmo percurso sete vezes. O Quadro 2 apresenta uma classificação para a variabilidade do tempo, segundo o valor do desvio-padrão.
- Quadro 1:
- Quadro 2:
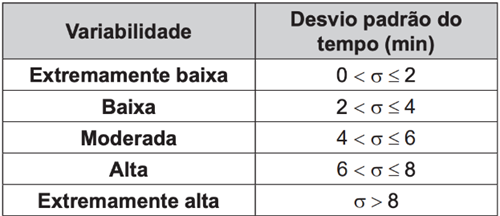
Com base nas informações apresentadas nos quadros, a variabilidade do tempo é
A) extremamente baixa.
B) baixa.
C) moderada.
D) alta.
E) extremamente alta.
Alternativa B
Calculando a média:
\(\overline{x}=\frac{48+54+50+46+44+52+49}{7}\)
\(\overline{x}=\frac{343}{7}=49\)
Calculando o desvio-padrão:
\(DP=\sqrt{\frac{\left(48-49\right)^2+\left(54-49\right)^2+\left(50-49\right)^2+\left(46-49\right)^2+\left(44-49\right)^2+\left(52-49\right)^2+\left(49-49\right)^2}{7}}\)
\(DP=\sqrt{\frac{1+25+1+9+25+9+0}{7}}\)
\(DP=\sqrt{\frac{700}{7}}\)
\(DP=\sqrt{10}\)
Sabemos que a raiz quadrada de 10 está entre 2 e 4, então a variabilidade é baixa.
(Enem) Marco e Paulo foram classificados em um concurso. Para classificação no concurso, o candidato deveria obter média aritmética na pontuação igual ou superior a 14. Em caso de empate na média, o desempate seria em favor da pontuação mais regular. No quadro a seguir, são apresentados os pontos obtidos nas provas de Matemática, Português e Conhecimentos Gerais, a média, a mediana e o desvio-padrão dos dois candidatos.
Dados dos candidatos no concurso:
O candidato com pontuação mais regular, portanto, mais bem classificado no concurso, é:
A) Marco, pois a média e a mediana são iguais.
B) Marco, pois obteve menor desvio-padrão.
C) Paulo, pois obteve a maior pontuação da tabela, 19 em Português.
D) Paulo, pois obteve maior mediana.
E) Paulo, pois obteve maior desvio-padrão.
Alternativa B
A média dos candidatos é a mesma, portanto, o que possui menor desvio-padrão será o candidato mais bem classificado no concurso, que, no caso, é o Marco.
(Enem) O procedimento de perda rápida de “peso” é comum entre os atletas dos esportes de combate. Para participar de um torneio, quatro atletas da categoria até 66 kg, Peso-Pena, foram submetidos a dietas balanceadas e atividades físicas. Realizaram três “pesagens” antes do início do torneio. Pelo regulamento do torneio, a primeira luta deverá ocorrer entre o atleta mais regular e o menos regular quanto aos “pesos”. As informações com base nas pesagens dos atletas estão no quadro.
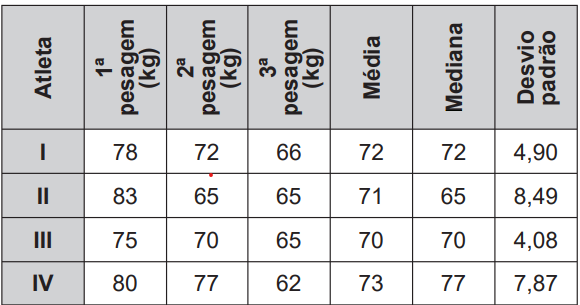
Após as três “pesagens”, os organizadores do torneio informaram aos atletas quais deles se enfrentariam na primeira luta.
A primeira luta foi entre os atletas:
A) I e III
B) I e IV
C) II e III
D) II e IV
E) III e IV
Alternativa C
O atleta mais regular é o que tem menor desvio-padrão, que é o atleta III. O atleta menos regular é o que tem maior desvio-padrão, que é o atleta II. Então a primeira luta será entre II e III.
