Exercícios sobre diferenças entre figuras planas e espaciais
Sobre as figuras planas, assinale a alternativa correta.
a) Uma figura é considerada plana quando possui exatamente uma dimensão.
b) Uma figura é considerada plana quando é possível medir seu comprimento, largura e profundidade.
c) São exemplos de figuras planas: cubo, quadrado e paralelogramo.
d) São exemplos de figuras planas: círculo, circunferência, setor circular e arco.
e) Não são exemplos de figuras planas: cubo, paralelepípedo e paralelogramo.
a) Incorreta!
Uma figura é considerada plana quando possui duas dimensões.
b) Incorreta!
Uma figura é considerada plana quando é possível medir comprimento e largura, comprimento e profundidade ou largura e profundidade. O importante é que as figuras planas sejam bidimensionais, isso significa que é possível obter duas medidas a partir delas.
c) Incorreta!
O cubo não é um exemplo de figura plana.
d) Afirmativa correta!
e) Incorreta!
O paralelogramo é um exemplo de figura plana.
Alternativa D
Avalie as alternativas a seguir e marque aquela que descreve corretamente a construção de figuras geométricas.
a) É possível construir um círculo no “espaço” unidimensional.
b) É possível construir um cubo tendo como espaço para isso apenas o plano.
c) É possível construir um quadrado dentro de uma reta.
d) É possível construir um cone dentro do espaço unidimensional.
e) É possível construir uma esfera dentro do espaço tridimensional.
Somente é possível construir figuras geométricas em um espaço se o número de dimensões da figura for igual ou inferior ao número de dimensões do espaço. Assim, não é possível construir um círculo no espaço unidimensional, nem um cubo no plano, nem um quadrado dentro da reta, nem um cone no espaço unidimensional.
A única alternativa viável é a construção de uma esfera dentro do espaço tridimensional. É claro que não estamos considerando planificações, nem representações planas de figuras tridimensionais.
Alternativa E
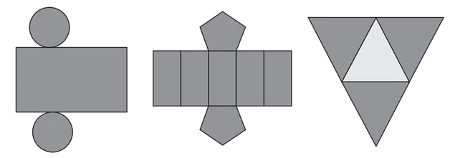
Enem-2012 – Maria quer inovar sua loja de embalagens e decidiu vender caixas com diferentes formatos. Nas imagens apresentadas, estão as planificações dessas caixas.
Quais serão os sólidos geométricas que Maria obterá a partir dessas planificações?
a) Cilindro, prisma de base pentagonal e pirâmide.
b) Cone, prisma de base pentagonal e pirâmide.
c) Cone, tronco de pirâmide e prisma.
d) Cilindro, tronco de pirâmide e prisma.
e) Cilindro, prisma e tronco de cone.
A planificação de um cilindro é composta por dois círculos e um retângulo. Um prisma de base pentagonal possui em sua planificação dois pentágonos e cinco retângulos; e uma pirâmide de base triangular possui a planificação formada por quatro triângulos. Essa é justamente a configuração das planificações das caixas, por isso, elas formam: um cilindro, um prisma de base pentagonal e uma pirâmide.
Alternativa A
A respeito da planificação de uma pirâmide regular de base hexagonal, assinale a alternativa correta.
a) A planificação de uma pirâmide de base hexagonal é um hexágono.
b) Nas planificações de pirâmides, o número de triângulos observados é sempre maior do que o número de lados de sua base.
c) Como a pirâmide é regular, todas as suas faces laterais são congruentes.
d) Uma das faces laterais da pirâmide é um hexágono.
e) Não é possível calcular volume de pirâmides com bases que não são triângulos ou quadriláteros.
a) Incorreta!
A planificação de uma pirâmide de base hexagonal é composta por um hexágono e seis triângulos.
b) Incorreta!
O número de triângulos observados em uma planificação de uma pirâmide sempre é igual ao número de lados da base desse sólido.
c) Correta!
d) Incorreta!
O hexágono é a base da pirâmide e todas as suas faces laterais são triângulos.
e) Incorreta!
É possível calcular o volume de qualquer pirâmide.
Alternativa C
