Exercícios sobre Equação do 1º grau com duas incógnitas
Exercícios propostos e soluções de equações do 1º grau com duas incógnitas.
Publicado por: Franciely Jesus GuedesQuestões
-
Questão 1
Nos itens que se seguem, determine duas soluções distintas para as equações:
a) 5x-2y=9
b)
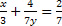
a) Vamos supor que x=0, substituindo na equação temos 5*0-2y=9, que é equivalente a -2y=9. Então, basta isolar a variável y, assim
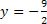 . Logo, uma solução é o par
. Logo, uma solução é o par 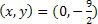 .
.
Agora, para encontrar outra solução, podemos supor y=0, após substituirmos na equação original temos 5x=9. Isolando a variável x, temos que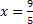 . Portanto, outra solução seria o par
. Portanto, outra solução seria o par 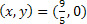
b) Vamos supor que x=0, substituindo na equação temos
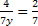 . Então basta isolar a variável y, assim
. Então basta isolar a variável y, assim 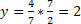 . Logo, uma solução é o par (x,y)=(0,2).
. Logo, uma solução é o par (x,y)=(0,2).
Agora, para encontrar outra solução, não podemos supor y=0, pois assim o denominador da segunda parcela seria zero, e não existe divisão por zero. Assim, vamos supor y=1, após substituirmos na equação original, temos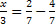 . Isolando a variável x e fazendo a subtração, temos que
. Isolando a variável x e fazendo a subtração, temos que 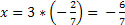 . Portanto, outra solução seria o par
. Portanto, outra solução seria o par 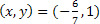 .
. -
Questão 2
Em uma partida de futebol, Lucas e Marcelo foram os únicos que marcaram gols pelo time anfitrião. Sabendo que o jogo foi vencido por 4x0, expresse essa situação por meio de uma equação de 1º grau com duas incógnitas e identifique todas as possíveis soluções.
Como não sabemos quantos gols cada jogador marcou, vamos imaginar que x representa a quantidade de gols marcada por Lucas e y representa a quantidade de gols marcada por Marcelo. Sabemos que a soma dessas quantidades é igual a 4. Então para escrever em forma de equação de 1º grau com duas incógnitas basta fazer x+y=4. Agora, para encontrar a solução dessa equação não podemos supor nem que x nem que y sejam iguais a zero e nem que sejam iguais a quatro, isso porque sabemos que os dois marcaram gols. Então vamos supor x=1, neste caso, teríamos y=4-1=3. Se x=2, temos que y=4-2=2 e, por fim, se x=3 temos que y=4-3=1. Portanto, as únicas soluções para essas equações são: Lucas ter marcado um gol e Marcelo ter marcado três gols, ou ambos terem marcado dois gols, ou então Lucas ter marcado três gols e Marcelo ter marcado somente um gol.
-
Questão 3
Todas as possíveis soluções de uma equação de 1º grau com duas incógnitas estão sobre uma reta no plano cartesiano. Sabendo disso, esboce o gráfico de soluções da equação .
Sabendo que quaisquer dois pontos determinam uma reta, vamos encontrar dois pontos que sejam soluções da equação. Para isso, basta fazer x1=0, e então
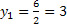 e já temos o ponto (x1,y1)=(0,3). E, fazendo y2=0, temos
e já temos o ponto (x1,y1)=(0,3). E, fazendo y2=0, temos 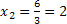 e assim, o segundo ponto é (x2,y2)=(2,0). Agora é só colocar os pontos no plano cartesiano e traçar a reta que passa por eles. Essa reta corresponde a todas as possíveis soluções da equação.
e assim, o segundo ponto é (x2,y2)=(2,0). Agora é só colocar os pontos no plano cartesiano e traçar a reta que passa por eles. Essa reta corresponde a todas as possíveis soluções da equação.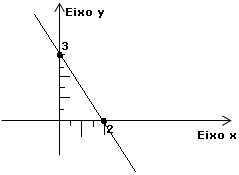
-
Questão 4
Escreva duas equações distintas de 1º grau com duas incógnitas que apresentem como solução o ponto (3,4).
Para encontrar duas equações que tenha como solução o ponto (x,y)=(3,4), podemos operar x e y de diversas formas, por exemplo, somar as variáveis, assim temos x+y=3+4=7, então a primeira equação pode ser x+y=7. E para encontrar a segunda equação, podemos dobrar o valor de x e subtrair do triplo de y, assim temos 2x-3y=2*3-3*4=6-12=-6 e a segunda equação seria 2x-3y=-6. Note que podemos obter infinitas soluções seguindo esse raciocínio.