Exercícios sobre equação exponencial
O valor de x que satisfaz a equação \(3^{x+1}=81\) é:
A) 1
B) 2
C) 3
D) 4
E) 5
Alternativa C
Primeiro vamos igualar as bases. Sabemos que 81 = \(3^4\), então temos que:
\(3^{x+1}=3^4\)
Após igualar as bases, igualamos os expoentes:
\(x+1=4\)
\(x=4-1\)
\(x=3 \)
Então o valor de x que satisfaz a equação exponencial é \(x=3 \).
Analise as equações representadas a seguir:
I. \(3x+4=x^3\)
II. \(x^2+2x+1=0\)
III. \(2^x+1=5\)
Analisando as equações, podemos classificar como equação exponencial:
A) somente a equação I.
B) somente a equação II.
C) somente a equação III.
D) somente as equações I e III.
E) as equações I, II e III.
Alternativa C
Para que a equação seja exponencial, é necessário que tenha uma incógnita no expoente. Analisando as equações citadas, somente a equação III satisfaz a definição de equação exponencial.
Calcule o valor de x na equação:
\(2^{x+1}+2^x+5=101\)
A) x = 1
B) x = 2
C) x = 3
D x = 4
E) x = 5
Alternativa E
Primeiro isolaremos a incógnita:
\(2^{x+1}+2^x+5=101\)
\(2^{x+1}+2^x=101-5\)
\(2^{x+1}+2^x=96\)
Utilizando a propriedade de potência, temos que:
\(2^x⋅2+2^x=96\)
\(2^x (2+1)=96\)
\(2^x⋅3=96\)
\(2^x=\frac{96}3\)
\(2^x=32\)
Sabemos que 32 = \(2^5\), logo, temos que:
\(2^x=2^5\)
\(x=5\)
Durante os seus estudos, um biólogo constatou que o número de bactérias de uma cultura após t horas pode ser descrito pela equação \(N(t)=N_0⋅3^t\), em que \(N_0\) é o número inicial de bactérias. Se o número de bactérias de uma certa cultura é de igual a 800, após quanto tempo teremos um total de 583.200 bactérias?
A) 6 horas
B) 8 horas
C) 10 horas
D) 12 horas
E) 16 horas
Alternativa A
Sabendo que \(N_0=800\), então temos que:
\(800⋅3^t=583.200\)
\(3^t=\frac{583.200}{800}\)
\(3^t=729\)
\(3^t=3^6\)
\(t = 6\)
Conhecendo a equação exponencial \(2^{-x^2-2x+5}=4\), podemos afirmar que o produto entre as soluções dessa equação é igual a:
A) 1
B) -3
C) 3
D) 4
E) -4
Alternativa B
Primeiro igualamos a base:
\(2^{-x^2-2x+5}=4\)
\(2^{-x^2-2x+5}=2^2\)
Agora que a base é igual, podemos igualar os expoentes:
\(-x^2-2x+5=2\)
\(-x^2-2x+5-2=0\)
\(-x^2-2x+3=0\)
Resolvendo essa equação por soma e produto, temos que:
\(x_1+x_2=-\frac{(-2)}{-1}=-2\)
\(x_1⋅x_2=\frac{3}{-1}=-3\)
Os números que satisfazem as duas equações ao mesmo tempo são -3 e 1, então x = -3 ou x = 1. Dessa forma, o produto entre essas soluções é igual a \((-3)⋅1=-3\).
Conhecemos como meia-vida o tempo que determinado elemento químico radioativo leva para perder metade da sua massa atual. Um elemento radioativo utilizado no tratamento apresenta meia-vida de 5 horas. Se a massa utilizada em um hospital para tratamento de um paciente for inicialmente de 100 gramas, após quantas horas ela seria reduzida para 6,25 gramas?
A) 4 horas
B) 10 horas
C) 20 horas
D) 30 horas
E) 60 horas
Alternativa C
A nova massa pode ser dada pela fórmula:
\(m=\frac{m_0}{2^t }\)
Em que t é a quantidade de períodos de meia-vida necessária para que a massa \(m_0\) se reduza à massa m. Então temos que:
\(6,25=\frac{100}{2^t }\)
\(2^t⋅6,25=100\)
\(2^t=\frac{100}{6,25}\)
\(2^t=16\)
\(2^t=2^4\)
\(t=4\)
Se há 4 períodos de 5 horas, então o tempo necessário é de 20 horas.
A equação \(P(n)=Q⋅2^{0,05n}\) nos da o número de habitantes P de determinada região, em função do número de anos n, sendo Q a quantidade de habitantes em determinado ano. Se em 2000 a população nessa cidade era de 138.000 habitantes, quanto tempo levará para que a população seja maior que 552.000 habitantes?
A) 40 anos
B) 42 anos
C) 44 anos
D) 46 anos
E) 48 anos
Alternativa A
Sabemos que Q = 138.000 e que P(n) > 522.000. Então temos que:
\(552.000<138.000⋅2^{0,05n}\)
\(\frac{552.000}{138.000}<2^{0,05n}\)
\(4<2^{0,05n}\)
\(2^2<2^{0,05n}\)
\(2<0,05n\)
\(\frac{2}{0,05}<n\)
\(40<n \)
Logo, é necessário que se passe mais de 40 anos.
Dados \(a=0,5^{3x+4}\) e \(b=(\frac{1}{2})^{8x-6}\), o valor de x que faz com que a = b é:
A) 1
B) 2
C) 3
D) 4
E) 5
Alternativa B
Igualando as equações, temos que:
\(0,5^{3x+4}=(\frac{1}{2})^{8x-6}\)
\((\frac{1}{2})^{3x+4}=(\frac{1}{2})^{8x-6}\)
\(3x+4=8x-6\)
\(3x-8x=-6-4\)
\(-5x=-10\)
\(x=\frac{-10}{-5}\)
\(x=2\)
Durante os seus estudos, um biólogo percebeu que o número de sementes de uma fruta quadruplica a cada semana. Se inicialmente havia 3 sementes, após quanto tempo haverá um total de 3072 sementes?
A) 2 semanas
B) 3 semanas
C) 4 semanas
D) 5 semanas
E) 6 semanas
Alternativa D
Montando a equação exponencial, com n representando o número de semanas, temos que:
\(3⋅4^n=3072\)
\(4^n=\frac{3072}3\)
\(4^n=1024\)
\(2^2n=2^{10}\)
\(2n=10\)
\(n=\frac{10}2\)
\(n = 5\)
A professora Kárita decidiu abrir um canal no YouTube para expor as suas videoaulas de Geografia. Na primeira semana do canal, ela obteve 100 seguidores, e, posteriormente, ela percebeu que o número de seguidores dobrava a cada mês. Se esse padrão for mantido, quanto tempo será necessário para que ela alcance o total de 1600 seguidores?
A) 1 mês
B) 2 meses
C) 3 meses
D) 4 meses
E) 5 meses
Alternativa D
Montando a equação exponencial, com n representando o número de seguidores, temos que:
\(100⋅2^n=1600\)
\(2^n=\frac{1600}{100}\)
\(2^n=16\)
\(2^n=2^4\)
\(n = 4 \)
Considerando uma matéria radioativa, é comum que a sua massa se desintegre ao decorrer do tempo de forma exponencial. Um elemento X possui meia-vida de 10 anos, isso significa que, após 10 anos, ele terá metade da matéria desintegrada. Se havia 500 gramas desse elemento, quanto tempo levará para que restem 62,5 gramas?
A) 20 anos
B) 30 anos
C) 40 anos
D) 50 anos
Alternativa B
A massa, ao decorrer do tempo, é dada por:
\(m=\frac{500}{2^t }\)
Se a matéria é de 62,5 gramas, então temos que:
\(62,5=\frac{500}{2^t }\)
\(2^t=\frac{500}{62,5}\)
\(2^t=8\)
\(2^t=2^3\)
\(t=3\)
Como são 3 ciclos de meia-vida, então serão necessários 30 anos.
(Enem) Admita que um tipo de eucalipto tenha expectativa de crescimento exponencial, nos primeiros anos após seu plantio, modelado pela função \(y(t)=a^{t-1}\), na qual y representa a altura da planta em metro, t é considerado em ano, e a é uma constante maior que 1. O gráfico representa a função y.
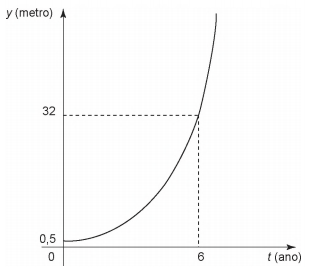
Admita ainda que y(0) fornece a altura da muda quando plantada, e deseja-se cortar os eucaliptos quando as mudas crescerem 7,5 m após o plantio.
O tempo entre a plantação e o corte, em ano, é igual a
A) 3
B) 4
C) 6
D) \(log_2 7\)
E) \(log_2 15\)
Alternativa B
Como y(0) nos dá a altura inicial, sabemos que ela é igual a 0,5, ou seja a = 0,5. Assim, temos que:
\(y(0)=a^{t-1}=0,5\)
\(a^{0-1}=0,5\)
\(a^{-1}=0,5\)
\(\frac{1}a=0,5\)
\(\frac{1}a=\frac{1}2\)
\(a=2\)
Sabendo que a = 2, e a árvore cresceu 7,5 m, com altura inicial de 0,5 m, então ela atingiu 8 m. Assim:
\(y(t)=2^{t-1}\)
\(8=2^{t-1}\)
\(2^3=2^{t-1}\)
\(3=t-1\)
\(t-1=3\)
\(t=3+1\)
\(t=4\)
