Exercícios sobre Equação Logarítmica
Resolva log3 (5x2 – 6x + 16) = log3 (4x2 + 4x – 5).
Respeitando a condição de existência, temos:
5x2 – 6x + 16 = 4x2 + 4x – 5 > 0
Agora basta utilizar a fórmula de Bhaskara:
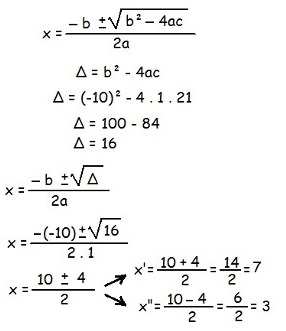
Substituindo x por 7 e 3 na condição de existência, verificamos que ela é verdadeira.
Resolva a equação encontrando o valor de x: log3/5 ( 2x² – 3x + 2) = 0.
Respeitando a condição de existência, temos:
2x2 – 3x + 2 > 0
Resolvendo a equação logarítmica:
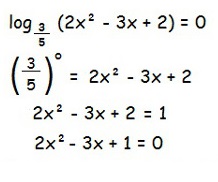
Agora basta utilizar a fórmula de Bhaskara:
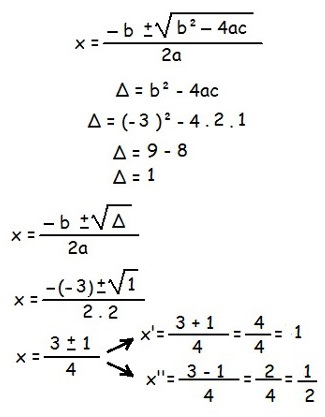
Substituindo x por 1 e ½ na condição de existência, verificamos que a condição é cumprida.
Encontre o valor de x na equação: log√5 [ 3 + 2 . log3 (x – 1)] = 2.
Respeitando a condição de existência:
3 + 2 . log3 (x – 1) > 0
Resolvendo a equação logarítmica:
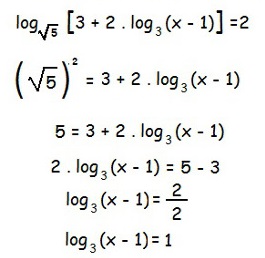
Agora resolvemos a nova equação logarítmica que surgiu, lembrando que, nesse caso, também há uma condição de existência, x – 1 > 0.
31 = x – 1
x = 3 + 1
x = 4
Substituindo x por 4, verificamos que a condição de existência é válida.
Resolva a equação: (log2 x)² – 15 = 2 . log2 x.
Para resolver a equação, é preciso considerar log2 x = y, portanto:
(log2 x)2 – 15 = 2 . log2 x
y2 – 15 = 2y
y2 – 2y – 15 = 0
A partir da fórmula de Bhaskara, temos:
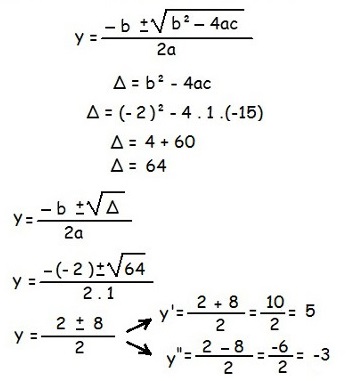
Mas y = log2 x, então:
-
Se y' = 5 → log2 x = 5 → 25 = x → x' = 32
-
Se y'' = – 3 → log2 x = – 3 → 2-3 = x → x'' = ⅛
Substituindo x por 32 e ⅛ na condição de existência, verificamos que ela é verdadeira.
