Home
Exercícios de Matemática
Exercícios sobre esfera

Exercícios sobre esfera

Verifique seus conhecimentos por meio desta lista de exercícios sobre esfera, um sólido geométrico classificado como corpo redondo por possuir superfície arredondada. Publicado por: Raul Rodrigues de Oliveira

Imprimir

Questão 1

Dada uma esfera que possui raio medindo 3 cm, então o valor do volume dessa esfera é:

A) $18π\ cm^3$

B) $27π\ cm^3$

C) $36π\ cm^3$

D) $45π\ cm^3$

E) $54π\ cm^3$

Ver resposta

Resposta

Alternativa C.

Calculando o volume da esfera, temos que:

$V=\frac{4πr^3}3$

$V=\frac{4⋅π⋅3^3}3$

$V=\frac{4⋅π⋅27}3$

$V=4⋅π⋅9$

$V=36\ π\ cm^3$

Questão 2

Uma esfera tem volume de 1046,6 cm³. Se π = 3,14, então o raio dessa esfera mede aproximadamente:

A) 5,4 cm

B) 6,3 cm

C) 7,5 cm

D) 8,1 cm

E) 9,0 cm

Ver resposta

Resposta

Alternativa B.

Se V = 1046,6, então temos que:

$V=\frac{4πr^3}3$

$1046,6=\frac{4πr^3}3$

$1046,6=\frac{4⋅3,14⋅r^3}3$

$1046,6⋅3=4⋅3,14⋅r^3$

$3139,8=12,59r^3$

$\frac{3139,8}{12,59}=r^3$

$249,4=r^3$

$r=\sqrt[3]{249,4}$

$r= 6,29$

$r = 6,3\ cm$

Questão 3

Uma embalagem possui o formato de uma esfera com raio medindo 6 cm de diâmetro. Nessas condições, podemos afirmar que a área é de:

A) 27π

B) 36π

C) 45π

D) 54π

E) 63π

Ver resposta

Resposta

Alternativa B.

Calculando a área da esfera:

$A=4πr^2$

$A=4⋅π⋅3^2$

$A=4⋅π⋅9$

$A=36π$

Questão 4

Uma bola de basquete possui volume igual a 7234,56 cm³. Considerando π= 3,14, a medida do diâmetro dessa bola é:

A) 10 cm

B) 12 cm

C) 20 cm

D) 24 cm

E) 34 cm

Ver resposta

Resposta

Alternativa D.

Sabemos que:

$V=\frac{4}3 πr^3$

$7234,56=\frac{4}3⋅3,14r^3$

$\frac{7234,56}{3,14}=\frac{4}3 r^3$

$2304=\frac{4}3 r^3$

$2304⋅\frac{3}4=r^3$

$1728=r^3$

$r=\sqrt[3]{1728}$

$r= 12$

Como queremos o diâmetro, sabendo que ele é igual ao dobro do raio, d = $12 ⋅2 = 24$

Questão 5

Uma esfera metálica possui a área da sua superfície medindo 400π cm². Então, a medida do raio dessa esfera é igual a:

A) 5 cm

B) 7 cm

C) 10 cm

D) 12 cm

E) 40 cm

Ver resposta

Resposta

Alternativa C.

Com a fórmula da área, temos que:

$4πr^2=400π$

$r^2=\frac{400π}{4π}$

$r^2=100$

$r=\sqrt{100}$

$r= 10\ cm$

Questão 6

Sobre a esfera, julgue as afirmativas a seguir:

I. A esfera é um corpo redondo.

II. A esfera que possui raio medindo 3 cm possui raio igual ao comprimento.

III. O diâmetro da esfera é igual ao dobro do seu raio.

Marque a alternativa correta:

A) Somente a afirmativa I é falsa

B) Somente a afirmativa II é falsa

C) Somente a afirmativa III é falsa

D) Todas as afirmativas são verdadeiras

Ver resposta

Resposta

Alternativa D.

I. A esfera é um corpo redondo. (verdadeiro)

Sabemos que a esfera é um corpo redondo por ter superfície arredondada.

II. A esfera que possui raio medindo 3 cm possui raio igual ao comprimento. (verdadeiro)

Calculando o volume da esfera com raio igual a 3 cm e a sua área, temos que:

$V=\frac{4}3⋅πr^3=4πr^2$

$V=4πr^3=3⋅4πr^2$

$r^3=\frac{3⋅4πr^2}{4π}$

$r^3=3r^2$

$\frac{r^3}{r^2} =3$

$r= 3$

Quando o raio vale 3 unidades, então o volume e a área possuem o mesmo valor.

III. O diâmetro da esfera é igual ao dobro do seu raio. (verdadeiro)

Sabemos, por definição, que a medida do diâmetro é igual ao dobro da medida do raio.

Questão 7

Chamamos de cunha esférica o sólido geométrico formado pela rotação de um semicírculo quando essa rotação é menor que 360°, ou seja, 0 < θ < 360°.

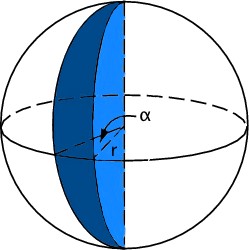
Ilustração de uma cunha esférica, uma das partes da esfera, em uma questão presente em uma lista de exercícios sobre esfera.

Se o ângulo for de 60° e o raio for igual a 3 cm, então o volume da cunha é de:

A) $π\ cm^3$

B) $6π\ cm^3$

C) $\frac{3}2 π\ cm^3$

D) $3π\ cm^3$

E) $\frac{4}3 π\ cm^3$

Ver resposta

Resposta

Alternativa B.

O volume da cunha é calculado por:

$V = \frac{\pi r^3 \theta}{270}$

$V = \frac{\pi \cdot 3^3 \cdot 60}{270}$

$V = \frac{\pi \cdot 27 \cdot 60}{270}$

$V=6π cm^3$

Questão 8

Marque a alternativa que melhor define a esfera:

A) A esfera é o conjunto de pontos que está a uma mesma distância r de um ponto no plano.

B) A esfera é o conjunto de pontos que estão a uma distância igual a r de um ponto no espaço.

C) A esfera é o conjunto de pontos que estão a uma distância igual ou menor que r de um ponto no espaço.

D) A esfera é o sólido geométrico que possui duas bases circulares e uma área lateral retangular.

E) A esfera é o sólido geométrico formado pela rotação de um triângulo em relação à sua altura.

F) A esfera é o sólido geométrico que possui duas bases circulares.

Ver resposta

Resposta

Alternativa C.

Sabemos que a esfera é a coleção de pontos no espaço que está a uma distância menor ou igual ao raio em relação ao seu ponto de origem.

Questão 9

(Enem) Peças metálicas de aeronaves abandonadas em aeroportos serão recicladas. Uma dessas peças é maciça e tem o formato cilíndrico, com a medida do raio da base igual a 4 cm e a da altura igual a 50 cm. Ela será derretida, e o volume de metal resultante será utilizado para a fabricação de esferas maciças com diâmetro de 1 cm, a serem usadas para confeccionar rolamentos. Para estimar a quantidade de esferas que poderão ser produzidas a partir de cada uma das peças cilíndricas, admite-se que não ocorre perda de material durante processo de derretimento.

Quantas dessas esferas poderão ser obtidas a partir de cada peça cilíndrica?

A) 800

B) 1200

C) 2400

D) 4800

E) 6400

Ver resposta

Resposta

Alternativa D.

Calculando o volume do cilindro:

$V=πr^2⋅h=π4^2⋅50=800$

Calculando o volume da esfera:

$V=\frac{4πr^3}3=\frac{4⋅π⋅0,5^3}3=\frac{4⋅π⋅0,125}3=\frac{0,5π}3$

Dividindo o volume do cilindro pelo volume da esfera:

$\frac{800π}{\frac{0,5π}{3}}$

$800π⋅\frac{3}{0,5π}= 4800$

Questão 10

(Enem) Em um casamento, os donos da festa serviam champanhe aos seus convidados em taças com formato de um hemisfério (Figura 1), porém um acidente na cozinha culminou na quebra de grande parte desses recipientes. Para substituir as taças quebradas, utilizou-se um outro tipo com formato de cone (Figura 2). No entanto, os noivos solicitaram que o volume de champanhe nos dois tipos de taças fosse igual.

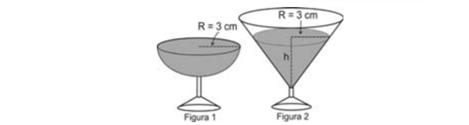
Ilustração de uma taça com formato de hemisfério ao lado de uma taça com formato de cone em um exercício sobre esfera.

Considere:

$V_{esfera}= \frac{4}3 πR^3\ e\ V_{cone}= \frac{1}3 πR^2 h$

Sabendo que a taça com o formato de hemisfério é servida completamente cheia, a altura do volume de champanhe que deve ser colocado na outra taça, em centímetros, é de

A) 1,33

B) 6,00

C) 12,00

D) 56,52

E) 113,04

Ver resposta

Resposta

Alternativa B.

O volume do hemisfério é igual à metade do volume da esfera. Então, temos que:

$\frac{4}6 πr^3=\frac{1}3 πr^2 h$

$\frac{4}6 π3^3=\frac{1}3 π⋅3^2⋅h$

$\frac{4}6 π⋅27=\frac{1}3⋅π⋅9⋅h$

$18π= 3πh$

$\frac{18π}{3π}=h$

$h= 6$

Questão 11

(Enem) Uma empresa que fabrica esferas de aço, de 6 cm de raio, utiliza caixas de madeira, na forma de um cubo, para transportá-las. Sabendo que a capacidade da caixa é de 13.824 cm³, então o número máximo de esferas que podem ser transportadas em uma caixa é igual a

A) 4.

B) 8.

C) 16.

D) 24.

E) 32.

Ver resposta

Resposta

Alternativa B.

Primeiro, calcularemos a medida da aresta do cubo:

$a^3=13824$

$a=\sqrt[3]{13824}$

$a=24$

O raio da esfera é de 6 cm, então o diâmetro é de 12 cm.

24 : 12 = 2

Como temos 3 dimensões, temos que 2³ = 8. Logo, caberão 8 esferas.

Questão 12

(Enem) Uma indústria de perfumes embala seus produtos, atualmente, em frascos esféricos de raio R, com volume dado por $\frac{4}3 π⋅R^3$ .

Observou-se que haverá redução de custos se forem utilizados frascos cilíndricos com raio da base $\frac{r}3$ , cujo volume será dado por $π⋅(\frac{R}{3})^2⋅h$ , sendo h a altura da nova embalagem.