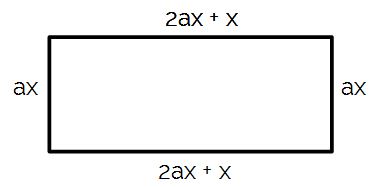Exercícios sobre fator comum em evidência
Para resolver estes exercícios sobre fator comum em evidência, devemos escrever a expressão na forma de produto.
Publicado por: Naysa Crystine Nogueira OliveiraQuestões
-
Questão 1
Agrupe os termos semelhantes nas expressões e fatore-as pelo método do fator comum em evidência.
a) ax2 + 2ax – 3ax2 + ax =
Para agrupar os termos, devemos colocar os de mesma parte literal próximos na expressão.
= 1ax2 – 3ax2 + 2ax + 1ax =
Some ou subtraia os coeficientes de mesma parte literal, ou seja, 1 – 3 e 2 + 1
= – 2ax2 + 3ax =
Devemos agora colocar em evidência os termos de menor grau, ou seja, de menor expoente, que se repetem: o ax.
= ax . (- 2x + 3)
b) ay3 + 4by – 16by + 5ay3 =
Vamos agrupar os termos semelhantes, ou seja, de mesma parte literal.
= 1ay3 + 5ay3 + 4by – 16by =
Some ou subtraia os coeficientes de mesma parte literal, ou seja, +1 + 5 e + 4 – 16.
= 6ay3 – 12by =Coloque em evidência o termo de menor grau que está se repetindo, que é o y.
= 6y . (ay2 - 2b)
c) by + ax + bx + ay =
Agrupe os termos que possuem algum elemento em comum.
= ay + by + ax + bx =
Coloque em evidência os elementos em comum.= y . (a + b) + x . (a + b) =
Coloque em evidência os termos que se repetem no produto de y . (a + b) e de x . (a + b), que é (a + b), e agrupe os outros termos entre parênteses, que é (y + x).
= (a + b) . (y + x)
-
Questão 2
Simplifique a expressão: n² + nx + nc + cx=
n² + nx + nc + cx=
Reúna de dois em dois observando o termo que se repete e coloque-o em evidência.
= n . (n + x) + c . (n + x)
Veja que (n + x) é igual em ambos os produtos; logo, coloque-o em evidência e agrupe os outros termos entre parênteses, que são (n + c).
= (n + x) . (n + c)
-
Questão 3
Fatore as expressões:
a) ax + bx + cx + dx =
Coloque em evidência o termo que está se repetindo, que é x.
= x . ( a + b + c + d)
b) 3bm – 3bx - 3bn =
Coloque em evidência o termo que está se repetindo, que é 3b.
=3b . (m – x – n)
c) 2x²y + 8xy – 4xyz =
Coloque em evidência o divisor de 2, 4, 8, que é 2, e o x e y, de menor grau/expoente.
= 2xy . ( x + 4 – 2z)
-
Questão 4
Obtenha a expressão do perímetro da figura abaixo e fatore caso seja necessário.
O perímetro é obtido pela soma das medidas dos lados de um polígono. Nessa questão, ele será representado pela letra P.
P = 2ax + x + 2ax + x + ax + ax
Agrupe os termos semelhantes, ou seja, de mesma parte literal.
P = 2ax + 2ax + 1ax + 1ax + 1x + 1x
Some os coeficientes dos termos semelhantes: 2 + 2 + 1 + 1 e 1 + 1
P = 6ax + 2x
Coloque em evidência o termo que se repete, que é x e o 2 (divisor de 6 e 2).
P = 2x . ( 3a + 1)