Exercícios sobre função constante
Sabendo que o domínio e o contradomínio das leis de formação a seguir são o conjunto dos números reais, marque a alternativa em que a lei de formação representa uma função constante.
A) f(x) = x
B) f(x) = 3x
C) f(x) = 3 – x
D) f(x) = 3
E) f(x) = x² + 3
Alternativa D.
Analisando as alternativas, podemos dizer que a função que é sempre igual a uma constante está representada na alternativa D, f(x) = 3.
Na imagem a seguir há uma representação do intervalo de uma função:
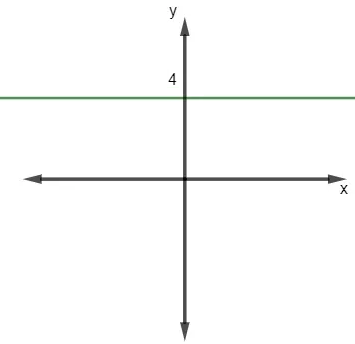
Analisando a representação para esse intervalo, podemos afirmar que essa função é:
A) crescente.
B) constante.
C) decrescente.
D) linear.
E) quadrática.
Alternativa B.
Analisando o gráfico da função para esse intervalo, podemos afirmar que ela é uma função constante, pois o valor da imagem é sempre o mesmo para todo valor de x.
Uma função afim pode ser crescente, decrescente ou constante. A função é classificada como constante se:
A) o seu coeficiente angular for um número maior que 0.
B) o seu coeficiente angular for exatamente igual a 0.
C) o seu coeficiente angular for menor que 0.
D) o seu coeficiente angular for igual a 1.
E) o seu coeficiente angular for um número entre 0 e 1.
Alternativa B.
A função é dita constante quando ela possui coeficiente angular exatamente igual a 0.
Analise as afirmativas a seguir:
I. Na função constante, o gráfico é sempre uma reta.
II. A reta que representa o gráfico da função constante é paralela ao eixo x.
III. Na função constante, o coeficiente angular é igual a 1.
Marque a alternativa correta:
A) Somente a afirmativa I é falsa.
B) Somente a afirmativa II é falsa.
C) Somente a afirmativa III é falsa.
D) Todas as afirmativas são verdadeiras.
Alternativa C.
I. Na função constante, o gráfico é sempre uma reta. (verdadeira)
De fato, o gráfico da função constante é uma reta.
II. A reta que representa o gráfico da função constante é paralela ao eixo x. (verdadeira)
A reta que representa o gráfico da função afim é sempre paralela ao eixo x.
III. Na função constante, o coeficiente angular é igual a 1. (falsa)
O coeficiente angular da função constante é igual a 0.
No diagrama a seguir, está representada uma relação entre dois conjuntos.
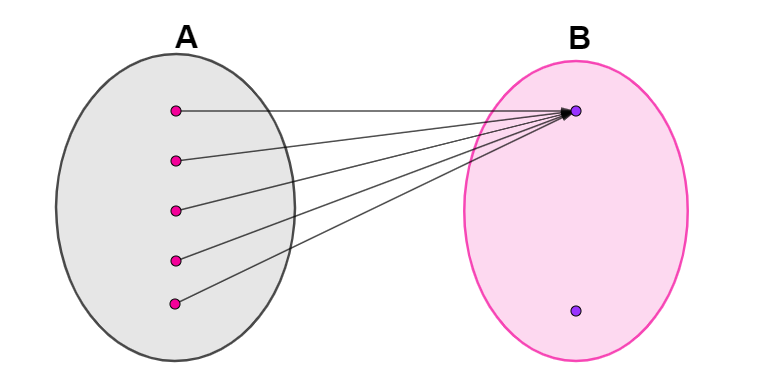
Analisando a imagem, podemos dizer que essa relação entre esses dois conjuntos
A) não é uma função, pois há elementos no conjunto B que não são correspondentes de nenhum elemento do conjunto A.
B) não é uma função, pois todos os elementos do conjunto A possuem o mesmo correspondente no conjunto B.
C) é uma função quadrática, pois todos os elementos do conjunto A possuem o mesmo correspondente no conjunto B.
D) é uma função constante, pois todos os elementos do conjunto A possuem o mesmo correspondente no conjunto B.
E) é uma função, porém não podemos afirmar que essa relação mostra uma função quadrática ou uma função constante.
Alternativa D.
O gráfico mostra uma função constante. Note que todos os elementos do conjunto A possuem um correspondente no conjunto B. Além disso, esse correspondente é o mesmo para todos os elementos, o que faz com que essa função seja constante.
O gráfico a seguir representa uma função.
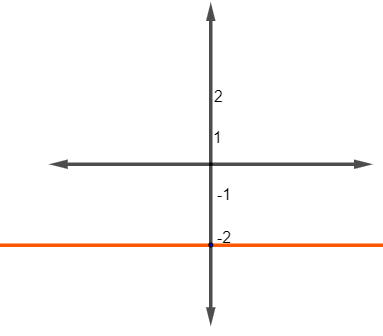
A lei de formação dessa função é:
A) f(x)=-2x
B) f(x)=2x
C) f(x)=-2
D) f(x)=2
E) f(x)=2x-2
Alternativa C.
Podemos perceber que essa função é uma função constante, que passa pelo ponto (0, -2). Sendo assim, a lei de formação dessa função é \( f\left(x\right)=-2\).
Marque a alternativa que corresponde ao gráfico da função fx=3
A)
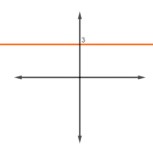
B)
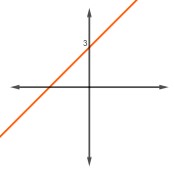
C)
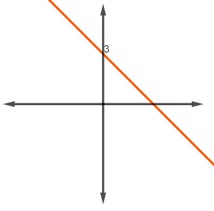
D)
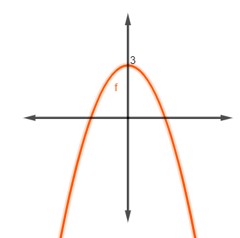
Alternativa A.
A função \(f\left(x\right)=3 \) é uma função constante, então a alternativa A é a que corresponde ao gráfico da função.
Uma função é considerada constante quando:
A) o domínio da função e o contradomínio da função são formados por números naturais.
B) a imagem for sempre a mesma para todo valor de x do domínio.
C) dados dois elementos diferentes no domínio, esses elementos possuírem imagens diferentes.
D) todo elemento do contradomínio for correspondente de pelo menos um elemento no domínio.
E) a função for injetora e sobrejetora, ou seja, bijetora.
Alternativa B.
A função é constante se a imagem for a mesma para todo valor do domínio.
Analise as leis de formação a seguir:
I. \(f\left(x\right)=2x-3\)
II.\(f\left(x\right)=5\)
III. \(f\left(x\right)=-3,4\)
Considerando o domínio e o contradomínio como o conjunto dos números reais, não pode ser considerada uma função constante:
A) somente a função I.
B) somente a função II.
C) somente a função III.
D) somente a função I e a função III.
Alternativa A.
A única lei de formação que não é de uma função constante é a função I. Perceba que as demais possuem valor sempre igual a uma constante real.
A função que possui lei de formação \(f\left(x\right)=\sqrt2\)é uma função:
A) racional.
B) exponencial.
C) constante.
D) quadrática.
E) natural.
Alternativa C.
Sabemos que \(\sqrt2\) é um número real. Note que a variável x não aparece na função. Sendo assim, para todo valor de x, a função tem a mesma imagem. Logo, essa função é uma função constante.
Conhecendo a função \(f\left(x\right)=\ 2\pi\), podemos afirmar que o valor numérico da função quando x = 3 é:
A) 3
B) 6
C) π
D) 2π
E) 3π
Alternativa D.
Como a função constante é igual a 2π, independentemente do valor do x, a imagem será a mesma. Logo, temos que \(f\left(3\right)=2\pi\).
(Vunesp) A representação gráfica de uma função constante, com o maior domínio possível, é uma
A) reta paralela ao eixo das ordenadas.
B) reta paralela ao eixo das abscissas.
C) reta não paralela ao eixo das abscissas, não paralela ao eixo das ordenadas e contendo o ponto (0, 0).
D) reta não paralela ao eixo das abscissas, não paralela ao eixo das ordenadas e não contendo o ponto (0, 0).
E) parábola, contendo o ponto (0, 0).
Alternativa B.
A função constante possui representação gráfica paralela ao eixo das abscissas, conhecido também como eixo horizontal.
