Exercícios sobre função polinomial
Dada a função polinomial f(x) = x³ – 3x² + 2x – ½, determine os pares ordenados quando x = – 1, x = 0 e x = 1.
Para encontrar o valor de y correspondente a cada valor de x, é necessário substituir os valores dados de x na função polinomial de terceiro grau.
Para x = – 1:
f(x) = x³ – 3x² + 2x – ½
f(–1) = (–1)³ – 3.(–1)² + 2.(–1) – ½
f(–1) = –1 – 3 – 2 – ½
f(–1) = – 6 – ½
f(–1) = – 12 – 1
2
f(–1) = – 13
2
Para x = 0:
f(x) = x³ – 3x² + 2x – ½
f(0) = 0³ – 3.0² + 2.0 – ½
f(0) = – ½
Para x = 1:
f(x) = x³ – 3x² + 2x – ½
f(1) = 1³ – 3.1² + 2.1 – ½
f(1) = 1 – 3 + 2 – ½
f(1) = – ½
Portanto, os pontos ordenados são (– 1, –13/2), (0, –½) e (1, – ½).
Determine os valores de a, b, c e d para que as funções polinomiais f(x) = 9x³ + (2 – a)x² – 3x + 2 e g(x) = (b/2)x³ + 7x² – 4cx + 3d/2 sejam iguais.
Para resolver essa questão, é preciso igualar as funções polinomiais de modo que os coeficientes sejam idênticos:
9x³ + (2 – a)x² – 3x + 2 = (b/2)x³ + 7x² – 4cx + 3d/2
9x³ + (2 – a)x² – 3x + 2 = (b/2)x³ + 7x² – 4cx + 3d/2
9 = b/2
b = 9.2
b = 18
2 – a = 7
– a = 7 – 2
a = – 5
– 3 = – 4c
c = ¾
2 = 3d/2
3d = 2.2
d = 4/3
Portanto, para que as funções polinomiais f(x) e g(x) sejam idênticas, é necessário que a = – 5, b = 18, c = ¾ e d = 4/3.
(Unicamp) Três planos de telefonia celular são apresentados na tabela abaixo:
|
Plano |
Custo fixo mensal |
Custo adicional por minuto |
|
A |
R$ 35,00 |
R$ 0,50 |
|
B |
R$ 20,00 |
R$ 0,80 |
|
C |
0 |
R$ 1,20 |
a) Qual é o plano mais vantajoso para alguém que utilize 25 minutos por mês?
b) A partir de quantos minutos de uso mensal o plano A é mais vantajoso que os outros dois?
Antes de resolver as questões propostas, é possível utilizar funções polinomiais do 1° grau para descrever o custo de cada plano. Dessa forma, a(x) = 0,5x + 35 é a função polinomial que representa o plano A, b(x) = 0,8x + 20 é a função que representa o plano B e c(x) = 1,2x é a função que representa o plano C (x representa o tempo em meses).
a) Para descobrir o valor que uma pessoa que utilize 25 minutos por mês pagará em cada plano, basta substituir x por 25 em cada função. Vejamos:
a(x) = 0,5x + 35
a(25) = 0,5.25 + 35
a(25) = 12,5 + 35
a(25) = 47,5
b(x) = 0,8x + 20
b(25) = 0,8.25 + 20
b(x) = 20 + 20
b(x) = 40
c(x) = 1,2x
c(25) = 1,2.25
c(25) = 30
Portanto, uma pessoa que utiliza 25 minutos mensais deverá utilizar o plano C.
b) Para identificar a partir de quantos minutos o Plano A é mais vantajoso, devemos igualar a função A às outras funções:
a(x) = b(x)
0,5x + 35 = 0,8.x + 20
0,5x – 0,8x = 20 – 35
– 0,3x = – 15
x = 15
0,3
x = 50
Para a utilização de 50 minutos por mês, os planos A e B têm o mesmo custo. Passando de 50 minutos, o plano A é mais vantajoso do que o plano B.
Vamos agora estabelecer uma comparação entre os planos A e C:
a(x) = b(x)
0,5x + 35 = 1,2x
0,5x – 1,2x = – 35
– 0,7x = – 35
x = 35
0,7
x = 50
Utilizando 50 minutos por mês, os gastos com os planos A e C são equivalentes, ultrapassando os 50 minutos, o plano A mostra-se mais vantajoso.
(UFG) Uma agência de turismo deseja fretar um ônibus de 50 lugares. Duas empresas, A e B, candidatam-se para fazer a viagem. Se for contratada a empresa A, o custo da viagem terá uma parte fixa de R$ 280,50, mais um custo, por passageiro, de R$ 12,00. Se for contratada a empresa B, o custo terá um valor fixo de R$ 250,00, mais um custo (C), por passageiro, dado por C(n) = 35 – 0,5n, onde n é o número de passageiros que fará a viagem.
De acordo com essas informações, julgue os itens a seguir.
(01) Caso contrate a empresa B, o custo máximo da viagem será de R$ 862,50.
(02) Se todos os lugares do ônibus forem ocupados, será mais caro contratar a empresa B.
(03) Para um mesmo número de passageiros, os valores cobrados pelas empresas A e B serão diferentes.
(04) Para um custo de R$ 700,50, a empresa A levará mais que o dobro de passageiros que a empresa B.
Vamos analisar cada item da questão, pois a resposta final desse exercício é a soma dos números dos itens corretos. Para tanto, é bom ressaltar a função que rege o custo de cada empresa. O custo da empresa A é dado pela soma da parte fixa de R$ 280,50 com o produto de R$12,00 pela quantidade n de passageiros, isto é, A(n) = 280,5 + 12.n. Já o custo da empresa B é dado através da soma do custo fixo de R$ 250,00 com o produto da função C(n) = 350 – 0,5n pela quantidade n de passageiros, isto é, B(n) = 250 + (35 – 0,5n).n → B(n) = – 0,5.n² + 35.n + 250.
(01) Utilizando a relação de máximo e mínimo de uma função de 2° grau, temos:
x = – b
2.a
x = – 35
2.(– 0,5)
x = 35
Vamos substituir o valor 35 na fórmula B(n) = 250 + 35.n – 0,5.n²:
B(n) = – 0,5.n² + 35.n + 250
B(35) = – 0,5.35² + 35.35 + 250
B(35) = – 612,5 + 1225 + 250
B(35) = 862,5
Portanto, o item (01) está correto.
(02) Os ônibus dispõem de 50 lugares. Para saber o custo caso todos os lugares sejam ocupados, basta substituir n por 50 em A(n) e B(n):
A(n) = 280,5 + 12.n
A(50) = 280,5 + 12.50
A(50) = 280,5 + 600
A(50) = 880,5
B(n) = 250 + 35.n – 0,5.n²
B(50) = 250 + 35.50 – 0,5.50²
B(50) = 250 + 1750 – 0,5.2500
B(50) = 250 + 1750 – 1250
B(50) = 750
Portanto, para a lotação máxima, a empresa A cobra um valor mais alto. Portanto, esse item é incorreto.
(03) Vejamos se existe alguma quantidade de passageiros em que o preço das empresas A e B é o mesmo. Para isso, vamos igualar as duas funções:
A(n) = B(n)
280,5 + 12.n = 250 + 35.n – 0,5.n²
0,5.n² +12.n – 35.n + 280,5 – 250 = 0
0,5.n² – 23.n + 30,5 = 0
Para resolver essa equação do 2° grau, basta utilizar a a fórmula de Bhaskara:
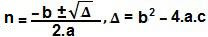
Δ = b² – 4.a.c
Δ = (– 23)² – 4.0,5.30,5
Δ = 529 – 61
Δ = 468
Como o valor de ∆ não possui raiz quadrada exata, não há uma quantidade de passageiros em que as duas empresas cobram o mesmo valor. Portanto, essa alternativa está correta.
(04) Vamos verificar quantos passageiros cada empresa leva com o valor de R$ 700,50.
Para a empresa A, temos:
A(n) = 280,5 + 12.n
700,5 = 280,5 + 12.n
12.n = 700,5 – 280,5
12.n = 420
n = 420
12
n = 35
Para a empresa B, temos:
B(n) = 250 + 35.n – 0,5.n²
700,5 = 250 + 35.n – 0,5.n²
0,5n² – 35.n + 450,5 = 0
Novamente, utilizando a fórmula de Bhaskara:
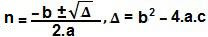
Δ = b² – 4.a.c
Δ = (– 35)² – 4.0,5.450,5
Δ = 1225 – 901
Δ = 324
n = – b ± √Δ
2.a
n = – (– 35) ± √324
2.0,5
n = 35 ± 18
1
n' = 35 + 18 = 53
n'' = 17
O valor de n' = 53 não é válido, pois a capacidade máxima do ônibus é de 50 passageiros. Portanto, com o valor de R$ 700,50, a empresa A carrega 35 passageiros, mais que o dobro da empresa B, que transporta apenas 17 passageiros. Sendo assim, esse item está correto.
A soma dos itens corretos é 01 + 03 + 04 = 08.
