Exercícios sobre Funções
Em uma indústria metalúrgica o custo de produção de uma peça automotiva corresponde a um custo fixo mensal de R$ 5 000,00 acrescido de um custo variável de R$ 55,00 por unidade produzida mais 25% de impostos sobre o custo variável. Considerando que o preço de venda dessa peça pela indústria aos comerciantes é de R$ 102,00, determine:
a) a função custo da produção de x peças.
b) a função receita referente a venda de x peças.
c) a função lucro na venda de x peças.
d) o lucro obtido com a venda de 500 unidades.
a) A função custo será dada pela somatória do custo fixo, do custo variável e do imposto cobrado de acordo com o custo variável.
Custo = 5000 + 55x + 0,25 * 55x
b) A função receita é dada por:
Receita = 102x
c) A função lucro é obtida subtraindo a função custo da função receita.
Lucro = 102x – (5000 + 55x + 0,25 * 55x)
Lucro = 102x – 5000 – 55x – 0,25 * 55x
Lucro = 102x – 55x – 13,75x – 5000
Lucro = 33,25x – 5000
Quando calculamos a função lucro determinamos uma expressão capaz de determinar o lucro líquido obtido da venda de x peças, isto descontados os custos de produção e os impostos municipais, estaduais e federais.
d) O lucro obtido com a venda de 500 unidades corresponde a:
f(x) = 33,25x – 5000
f(500) = 33,25 * 500 – 5000
f(500) = 16 625 – 5000
f(500) = 11 625
O lucro obtido é igual a R$ 11 625,00.
O IMC (índice de massa corpórea) é uma função matemática que determina se uma pessoa adulta é considerada gorda, obesa, normal ou está abaixo do peso, relacionando a massa da pessoa em quilogramas com o quadrado da medida da altura em metros. De acordo com a tabela a seguir determine a massa de uma pessoa com 1,90 metros de altura, para que seu IMC seja considerado normal.
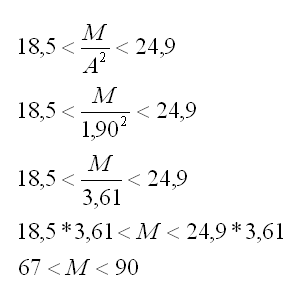
A massa de uma pessoa com 1,90 m de altura deve estar entre 67kg e 90kg, para ser considerada no peso ideal.
(UA–AM)
Após várias experiências em laboratórios, observou-se que a concentração de certo antibiótico, no sangue de cobaias, varia de acordo com a função y = 12x – 2x², em que x é o tempo decorrido, em horas, após a ingestão do antibiótico. Nessas condições, qual o tempo necessário para atingir o nível máximo de concentração desse antibiótico, no sangue dessas cobaias?
Vamos determinar as raízes da função y = 12x –2x², fazendo y = 0. Dessa forma temos:
–2x² + 12x = 0 *(–1)
2x² – 12x = 0
2x * (x – 6) = 0
2x = 0
x’ = 0
x – 6 = 0
x’’ = 6
As raízes da função são os valores onde o gráfico da função cruza o eixo das abscissas (x). Por ser uma função do 2º grau com concavidade voltada para baixo, devido o valor do coeficiente a ser um número negativo, a função atinge um valor máximo determinado pelo valor de yvértice, dado por:
.gif)
O vértice da função além de possuir representação no eixo y, também é representado no eixo x, pela expressão: .gif)
.gif)
Com esses pontos podemos traçar o gráfico da função y = 12x – 2x², e analisar o comportamento do antibiótico no sangue das cobaias.
.gif)
O gráfico seguido dos cálculos mostra que o antibiótico atinge o nível máximo de concentração em 3 horas.
(FGV-SP)
Um capital de R$ 12 000,00 foi aplicado em regime de juros compostos a uma taxa de 2,5% ao mês durante 12 meses. Ao retirar o montante resultante da aplicação a pessoa terá descontado do juro da aplicação 7% de imposto sobre aplicações financeiras envolvendo lucros mais 0,5% de contribuição para obras relacionadas à saúde pública, segurança e educação, totalizando 7,5% de descontos. Calcule o valor líquido dessa aplicação, isto é, o valor debitado os impostos.
Pela função dos juros compostos temos:
M = C * (1 + i)t
M = 12000 * (1 + 0,025)12
M = 12000 * 1,02512
M = 12000 * 1,344889
M = 16 138,67
Os impostos serão cobrados somente sobre os juros da aplicação. Veja:
J = M – C
J = 16 138,67 – 12000
J = 4 138,67
Valor do Imposto = 7,5% * 4 138,67 → 0,075 * 4 138,67 → R$ 310,40
O lucro líquido da aplicação será dado por
Mlíquido = M – I
Mlíquido = 16 138,67 – 310,40
Mlíquido = 15 828,27
O valor do lucro líquido, isto é, debitado os devidos impostos será de R$ 15 828,27.
