Exercícios sobre geometria espacial
Das formas geométricas a seguir, marque a alternativa que possui somente sólidos geométricos:
A) cilindro, círculo, cone
B) esfera, quadrado, triângulo
C) pirâmide, cone, prisma
D) circunferência, prisma, pirâmide
E) pirâmide, trapézio, esfera
Alternativa C
Analisando as alternativas, a única composta exclusivamente por nomes de sólidos geométricos é a C, que traz a pirâmide, o cone e o prisma.
A geometria espacial estuda os sólidos geométricos, divididos em dois grandes grupos. Nesses grupos, temos os corpos redondos e os poliedros. Sobre os sólidos geométricos, podemos afirmar que:
I. O cone é um caso particular de pirâmide, pois ele é também um poliedro.
II. A esfera não é um poliedro, pois ela não possui faces, logo, ela é um corpo redondo.
III. Os poliedros são sólidos geométricos cuja face é uma figura plana qualquer.
Marque a alternativa correta:
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Somente as afirmativas II e III são verdadeiras.
E) Todas as afirmativas são verdadeiras.
Alternativa B
I. O cone é um caso particular de pirâmide, pois ele é também um poliedro. (Falso)
O cone não é um poliedro, pois ele possui face circular, portanto, é um corpo redondo.
II. A esfera não é um poliedro, pois ela não possui faces, logo, ela é um corpo redondo. (Verdadeiro)
III. Os poliedros são sólidos geométricos cuja face é uma figura plana qualquer. (Falso)
Para que o sólido seja um poliedro, a sua face tem que ser um polígono. Vale lembrar que a circunferência, por exemplo, é uma figura plana, mas não é um poliedro, e, por isso, sólidos que possuem faces circulares não são poliedros.
Durante a aula de Matemática, o professor desafiou os seus estudantes a encontrarem objetos do cotidiano que possuam formato de um corpo redondo. Foi então que os alunos fizeram as listas a seguir:
⇒ Diana: frutas como maçã, limão e laranja; garrafa de refrigerante; e a lixeira cilíndrica da escola.
⇒ Renata: pneu dos carros; casquinha de sorvete; e chapéu de aniversário infantil.
⇒ Rogério: copo; garrafa de refrigerante; caixa de sapato.
⇒ Matheus: bola de futebol; globo ocular; cenoura; barril.
Ao analisar a lista dos estudantes, o professor percebeu que um dos alunos colocou um objeto que não é corpo redondo em sua lista. O aluno que fez isso foi:
A) Diana
B) Renata
C) Rogério
D) Matheus
Alternativa C
Podemos perceber que na lista do Rogério tem uma caixa de sapato. A caixa de sapato possui formato de um prisma, o prisma não é um corpo redondo, pois as suas faces são todas polígonos, logo, é um poliedro.
Durante o planejamento da construção de um posto de combustível, o engenheiro responsável estava pesquisando sobre o tamanho do reservatório de combustível a ser construído. O reservatório de um posto é sempre subterrâneo, e, nesse caso, ele deveria ter capacidade para 24 m³, comportando, portanto, 24 mil litros de combustível. Sabendo que esse reservatório possui formato de um paralelepípedo retângulo, o engenheiro o construiu com 3 metros de largura e 4 metros de comprimento para que ele tenha os 24 m³ desejados. A profundidade desse reservatório deve ser de:
A) 2 metros
B) 3 metros
C) 4 metros
D) 5 metros
E) 6 metros
Alternativa A
Se o reservatório possui formato de um paralelepípedo retângulo, a sua base é um retângulo, com 3 metros de largura e 4 metros de comprimento no caso. Para calcular o volume desse sólido, multiplicamos a área da base pela altura, e a área da base do retângulo é o produto das suas dimensões, logo, temos que:
\(V=A_b\cdot h\)
\(24\ =\ 3\ \cdot4\ \cdot h\)
\(24\ =\ 12h\)
\(h=\frac{24}{12}\)
\(h\ =\ 2\ metros\ \)
Então a profundidade do reservatório deve ser de 2 metros.
Nome da bola da Copa é escolhido pela primeira vez por torcedores: Brazuca
Brazuca supera Bossa Nova e Carnavalesca e ganha eleição com 77,8%. Pela primeira vez na história, o nome da bola da Copa do Mundo da Fifa foi escolhido pelos torcedores: Brazuca, que recebeu 77,8% de 1.119.539 votos e superou Bossa Nova (14,6%) e Carnavalesca (7,6%) como substituta da Jabulani em 2014, no Brasil.
Fonte: http://ge.globo.com/nome-da-bola-2014/noticia/2012/09/nome-da-bola-da-copa-e-escolhido-pela-primeira-vez-pela-torcida-brazuca.html
Ao analisar as medidas da bola Brazuca, foi constado que ela possui em média 437 gramas, circunferência máxima em média de 69 cm e raio médio de 10,98 cm. Considerando esse raio como 11 cm, nessas condições, podemos afirmar que o volume dessa bola é em média:
(use π=3)
A) 589 cm³
B) 1766 cm³
C) 2662 cm³
D) 4807 cm³
E) 5324 cm³
Alternativa E
Calculando o volume, temos que:
\(V=\frac{4\pi r^3}{3}\)
\(V=\frac{4\cdot3\cdot{11}^3}{3}\)
\(V=\frac{4\cdot3\cdot1331}{3}\)
\(V=4\cdot1331\)
\(V=5324\ cm^3\)
Um recipiente possui formato de um prisma com as dimensões a seguir:
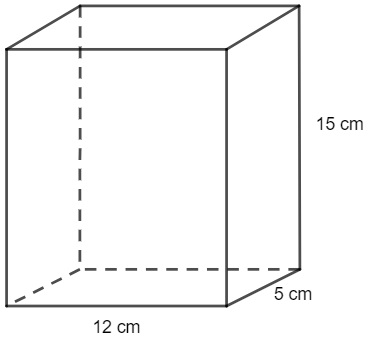
Sabendo que 2/3 do volume desse recipiente estão ocupados, então o volume não ocupado é igual a:
A) 200 cm³
B) 300 cm³
C) 500 cm³
D) 600 cm³
E) 900 cm
Alternativa B
Primeiro calcularemos o volume do prisma:
\(V=12\cdot5\cdot15\ \)
\(V=60\cdot15\ \)
\(V=900\ cm^3\)
Como 2/3 estão ocupados, então 1/3 não está, logo, dividindo 900 por 3, encontraremos o volume não ocupado desse sólido:
\(900 : 3 = 300 cm³\)
Uma caixa possui formato de um paralelepípedo reto com 25 cm de largura, 42 cm de altura e 36 cm de altura. A área total dessa caixa mede:
A) 3462 cm²
B) 6924 cm²
C) 8000 cm²
D) 9150 cm²
E) 10.369 cm²
Alternativa B
Calculando a área total, temos que:
\(A_T=2(ab+ac+bc)\)
\(A_T=2\cdot\left(25\cdot42+25\cdot36+36\cdot42\right)\)
\(A_T=2\cdot\left(1050+900+1512\right)\)
\(A_T=2\cdot3462\)
\(A_T=6924\ cm^2\)
O recipiente a seguir é uma forma geométrica:
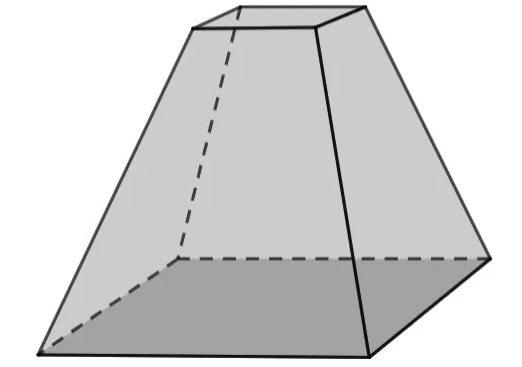
Analisando essa forma geométrica, um aluno fez três afirmativas:
I. Essa forma geométrica é um prisma de base quadrada.
II. Essa forma geométrica é um poliedro.
III. Essa forma geométrica não é um sólido geométrico.
Marque a alternativa correta:
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Todas as afirmativas são falsas.
Alternativa B
I. Essa forma geométrica é um prisma de base quadrada. (Falso)
O prisma tem que ter duas bases congruentes, nesse caso, esse sólido é um tronco de pirâmide e não um prisma.
II. Essa forma geométrica é um poliedro. (Verdadeiro)
Como esse sólido geométrico é fechado por faces com formato de polígonos, então ele, de fato, é um poliedro.
III. Essa forma geométrica não é um sólido geométrico. (Falso)
Note que se trata de uma figura espacial fechada por polígonos, logo, de um sólido geométrico.
Um reservatório de gás oxigênio foi construído no formato de um cilindro com 1,5 metros de altura e 60 centímetros de diâmetro. Nessas condições, podemos afirmar que o volume desse reservatório em metros cúbicos é de aproximadamente:
(use π=3,1)
A) 0,40
B) 0,42
C) 0,44
D) 0,46
E) 0,48
Alternativa B
O volume do cilindro é calculado por:
\(V=\pi r^2h\)
Sabemos que 60 centímetros de diâmetro correspondem a um raio de 30 centímetros, além disso, 30 centímetros equivalem a 0,3 metro. Então temos que:
\(V=3,1\cdot{0,3}^2\cdot1,5\)
\(V=3,1\ \cdot0,09\ \cdot1,5\ \)
\(V=0,4185\ m^3\)
Então o volume desse cilindro é de aproximadamente 0,42 m³.
(Enem) Em regiões agrícolas, é comum a presença de silos para armazenamento e secagem da produção de grãos, no formato de um cilindro reto, sobreposto por um cone, e dimensões indicadas na figura. O silo fica cheio, e o transporte dos grãos é feito em caminhões de carga cuja capacidade é de 20 m³. Uma região possui um silo cheio e apenas um caminhão para transportar os grãos para a usina de beneficiamento.
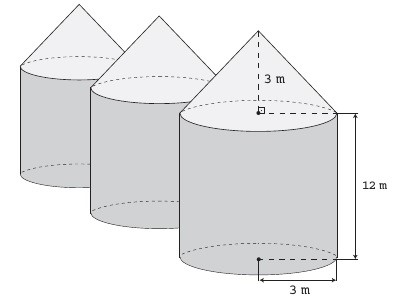
Utilize 3 como aproximação para π.
O número mínimo de viagens que o caminhão precisará fazer para transportar todo o volume de grãos armazenados no silo é:
A) 6
B) 16
C) 17
D) 18
E) 21
Alternativa D
Para calcular o volume do silo, vamos dividi-lo em um cone e um cilindro.
Calculando o volume do cone, temos que:
h = 3 metros
r = 3 metros
π = 3
\(V_{cone}=\frac{\pi r^2h}{3}\)
\(V_{cone}=\frac{3\cdot3^2\cdot3}{3}\)
\(V_{cone}=3^2\cdot3\)
\(V_{cone}=27\)
Agora calcularemos o volume do cilindro:
h = 12 metros
r = 3 metros
π = 3
\(V_{cilindro}=\pi r^2h\)
\(V_{cilindro}=3\cdot3^2\cdot12\)
\(V_{cilindro}=3\cdot9\cdot12\)
\(V_{cilindro}=27\cdot12\)
\(V_{cilindro}=324\)
Somando os dois volumes, temos que:
\(V=324+27=351\ m³\)
Sabemos que o caminhão leva 20 m³ por viagem, logo, temos que 351 : 20 = 17,5. Assim, serão necessárias 18 viagens.
(Enem) Um fazendeiro tem um depósito para armazenar leite formado por duas partes cúbicas que se comunicam, como indicado na figura. A aresta da parte cúbica de baixo tem medida igual ao dobro da medida da aresta da parte cúbica de cima. A torneira utilizada para encher o depósito tem vazão constante e levou 8 minutos para encher metade da parte de baixo.
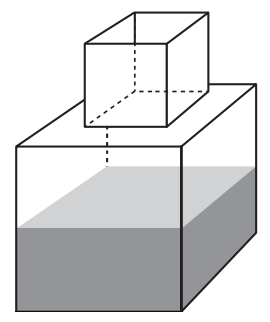
Quantos minutos essa torneira levará para encher completamente o restante do depósito?
A) 8
B) 10
C) 16
D) 18
E) 24
Alternativa B
Clamaremos de a a medida da aresta do cubo menor. Então temos que:
- aresta do cubo menor = a
- aresta do cubo maior = 2a
Calculando o volume do cubo, temos que:
- volume do cubo menor = a³
- volume do cubo maior (2a)³ = 8a³
Sabemos que o volume do cubo maior é igual a 8 vezes o volume do cubo menor. Se metade do cubo maior foi preenchida em 8 minutos, então, para preencher o cubo menor todo, serão necessários 16 minutos. Dividindo esse tempo por 8, encontramos o tempo necessário para encher o cubo menor, que é:
16 : 8 = 2 minutos
Então o tempo total necessário para preencher ambos os cubos é de
16 + 2 = 18 minutos
Como já se passaram 8 minutos, o tempo restante necessário será de 10 minutos.
(IFG) Considere um aquário em forma de paralelepípedo reto de base retangular, contendo água até certo nível e com dimensões da base, medindo 6 metros e 5 metros. Após a imersão de certo objeto sólido nesse aquário, o nível da água subiu 20 cm sem que água transbordasse. Nessas condições, é correto afirmar que o volume desse objeto sólido em metros cúbicos é de
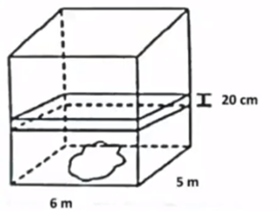
A) 0,6 m³.
B) 6 m³.
C) 60 m³.
D) 600 m³.
Alternativa B
Para calcular a área do objeto inserido no aquário, calcularemos a área da base vezes a altura a que o nível da água subiu. Note que a medida da base está em metros, mas que a altura do nível da água está em cm. Sabemos que 20 cm são 0,2 metro, então temos que:
\(V=6\cdot5\cdot0,2\ \)
\(V=30\cdot0,2\ \)
\(V=6{\ m}^3\)
