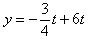Exercícios sobre Gráfico da Função de 2º Grau
Teste os seus conhecimentos: Faça exercícios sobre Gráfico da Função de 2º Grau e veja a resolução comentada.
Publicado por: Marcos Noé Pedro da SilvaQuestões
-
Questão 1
Sabe-se que o custo de C para produzir x unidades de certo produto é dado pela expressão C = x² – 80x + 3000. Calcule o a quantidade de unidades produzidas para que o custo seja mínimo e o valor desse custo mínimo.
O número de peças para que o custo seja mínimo será dado pelo cálculo de Xv e o valor deste custo mínimo será determinado pelo valor de x na função C = x² – 80x + 3000.
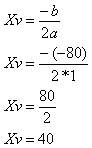
Custo da produção de 40 peças:
C = x² – 80x + 3000
C = 40² – 80 * 40 + 3000
C = 1600 – 3200 + 3000
C = 1.400Para obter um custo mínimo de R$ 1.400,00 a empresa deverá produzir exatamente 40 peças.
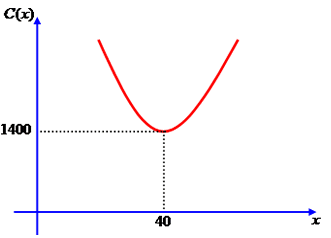
-
Questão 2
(PUCC-SP)
Um projétil da origem O (0,0), segundo um referencial dado, percorre uma trajetória parabólica que atinge sua altura máxima no ponto (2,4). Escreva a equação dessa trajetória.
A função do segundo grau que determina a trajetória parabólica de um projétil é:
y = ax2 + bx + c
Sabendo que a parábola passa pelo ponto (0,0) teremos:
y = ax2 + bx + c
0 = a02 + b0 + c
0 = c
Logo,
y = ax2 + bx
Utilizando a fórmula para o cálculo do y do vértice teremos:
yv = -∆
4a4 = -∆
4a-∆ = 4·4
a∆ = -16
aCalculando ∆ teremos:
∆ = b2 – 4ac
∆ = b2 – 4a0
∆ = b2
b2 = –16aUtilizando x do vértice:
xv = – b
2a2·2a = – b
b = –4a
Substituindo na equação anterior:
b2 = –16a
(–4a)2 = –16a
(–4)2a2 = –16a
16a2 = –16a
16a = –16
a = –1
Como b = –4a, então b = 4
Segue a equação do segundo grau com c = 0 e substituindo os valores de a e b:
y = –x2 + 4x
-
Questão 3
(FGV-SP)
O transporte aéreo de pessoas entre duas cidades A e B é feito por uma única companhia em um único voo diário. O avião utilizado tem 180 lugares, e o preço da passagem p relaciona-se com o número x de passageiros por dia pela relação p = 300 – 0,75x. Qual a receita máxima possível por viagem?
a) R$ 30 000,00
b) R$ 29 700,00
c) R$ 29 900,00
d) R$ 29 600,00
e) R$ 29 800,00
Temos que a receita máxima será dada por R(x) = p * x, onde R(x) = (300 – 0,75x) * x.
R(x) = – 0,75x² + 300. O número de passageiros responsáveis pela receita máxima será dado pelo valor do Xv na função, observe: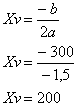
Como o avião comporta no máximo 180 passageiros, temos que a sua receita máxima acontecerá quando o avião estiver completamente lotado, isto é, com 180 passageiros. Calcularemos R(180) = (300 – 0,75 * 180) * 180.
R(180) = (300 – 135) * 180
R(180) = 165 * 180
R(180) = 29.700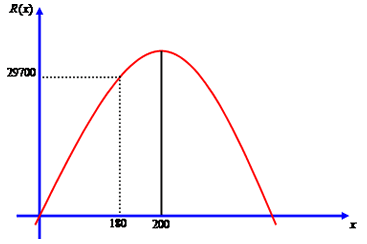
-
Questão 4
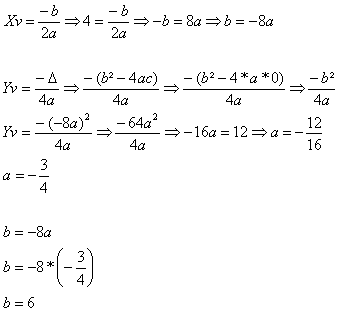
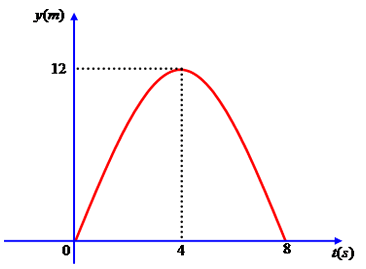
Com os valores dos coeficientes a = –3/4, b = 6 e c = 0 podemos formar a seguinte função: